Мерзликин Основы теории ядерных реакторов

Подставляя (5.4.14) и (5.5.1) в приведенную логическую формулу для pз, имеем:

Сравнивая (5.5.2) с начальным предположением (5.1.1), мы должны согласиться, что гипотеза (5.1.1) была не лишена оснований: pз действительно определяется, вопервых, величиной параметра реактора (позже убедимся, что параметр B2 имеет и геометрический смысл), а, во-вторых, - величиной комплексной характеристики замедляющих свойств среды активной зоны реактора, каковой и является возраст тепловых нейтронов (величина, равная шестой части среднего квадрата пространственного смещения замедляющегося нейтрона, то есть пропорционально связанная с величиной квадрата средней длины замедления).

Чем выше величина возраста тепловых нейтронов в реакторе (то есть чем хуже замедляющие свойства среды активной зоны), тем меньше величина вероятности избежания утечки замедляющихся нейтронов, поскольку величина возраста определяет толщину приграничного слоя активной зоны, из которого возможна утечка замедляющихся нейтронов. Чем меньше замедляющихся нейтронов располагают возможностью для утечки, тем выше доля замедляющихся нейтронов, которые останутся к концу замедления в активной зоне (то есть выше величина pз).

Что же касается другой величины, определяющей значение pз, - параметра реактора B2, то пока можно лишь сказать, что с геометрией активной зоны эта величина ка- ким-то образом связана, о чём свидетельствует её размерность - см-2. С непростым смыслом величины B2 ещё предстоит познакомиться подробнее.

5.6. Спектр замедляющихся нейтронов Ферми в гомогенной непоглощающей среде

Игнорируя вывод, приведём конечный вид спектра Ферми (с выводом можно познакомиться, например в [8]).

Распределение величины плотности потока замедляющихся нейтронов в непоглощающих средах (имеются в виду свойства не поглощать замедляющиеся нейтроны, а не тепловые) оказывается подчинённым закономерности:

Это выражение справедливо как для простой однородной среды, так и для сложных гомогенных сред, состоящих их нескольких сортов замедляющих ядер. В этом случае в формулу (5.6.1) подставляется сумма значений замедляющей способности k компонентов сложной среды

i=1

Учитывая классическую зависимость кинетической энергии нейтрона от его скорости (Е = mv2/2) и связь плотности потока и плотности нейтронов одинаковой скорости

выражение для спектра замедляющихся нейтронов можно записать так:

Таким образом, величина плотности замедляющихся нейтронов по энергиям в непоглощающей среде распределяется по закону "Е-3/2", то есть плавно возрастает с

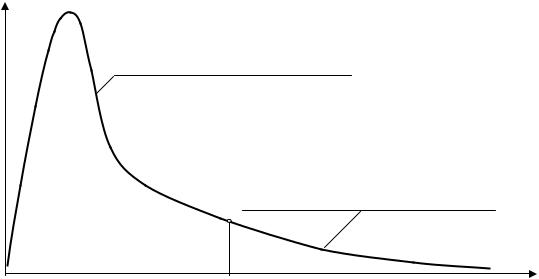
уменьшением энергии нейтронов в процессе их замедления, и столь же плавно (без скачков и изломов) переходит при Е = Ес в максвелловский спектр тепловых нейтронов

(рис.5.9).

В реальной замедляющей среде активной зоны, которой свойственно очень слабое поглощение замедляющихся нейтронов в замедлителе, и заметное поглощение их в топливе твэлов (где содержится резонансный захватчик замедляющихся нейтронов – уран-238), реальный спектр замедляющихся нейтронов проходит ниже изображённого на рис.5.9., но качественно выглядит так же.

n(E)

Спектр тепловых нейтронов (Максвелла)

Спектр замедляющихся нейтронов (Ферми)

E

Ec

Рис.5.9. Граница тепловых и замедляющихся нейтронов - энергия сшивки энергетических спектров Максвелла и Ферми (спектры ненормированные).

Уже отмечалось, что об энергетическом спектре нейтронов в реакторе имеет смысл говорить только для критического реактора, так как любой энергетический спектр в поглощающей среде имеет динамически равновесный характер: плотность нейтронов любой энергии Е поддерживается неизменной во времени в любом единичном объёме за счёт неизменной разницы скоростей:

-прихода замедляющихся нейтронов на уровень энергии Е из области более высоких энергий;

-ухода замедляющихся нейтронов с уровня энергии Е в область более низких энергий;

-появления в единичном объёме новых нейтронов энергии Е за счёт делений ядер (если таковые имеются в рассматриваемом единичном объёме);

-поглощения нейтронов при энергии Е (если в единичном объёме наличествуют поглотители) и

-утечки нейтронов энергии Е из единичного объёма (понимая под утечкой разницу скоростей ухода и прихода нейтронов с энергией Е в этом единичном объёме).

В рамках одногруппового возрастного приближения договорились считать, что поглощение в диапазоне энергий замедления отсутствует, а заметное поглощение замедляющихся нейтронов в реальных средах учитывать с помощью вероятности избежания резонансного захвата (ϕ). В этом приближении среда активной зоны поглощает только тепловые нейтроны. И если предполагать, что энергетический спектр тепловых нейтронов - максвелловского типа, величина и положение максимума на шкале энергий в нём явно должны зависеть от поглощающей характеристики среды (Σa) и замедляющей способности среды (ξΣs) в области энергий перехода от замедляющихся нейтронов к тепловым (то есть в области энергии сшивки Ес) и ниже (то есть в пределах самого спектра тепловых нейтронов).

Действительно, поскольку в тепловой области энергий микросечения поглощения изменяются по закону "1/v" (или"Е-1/2"), то основное поглощение тепловых нейтронов происходит при более низких энергиях левого крыла спектра Максвелла; чем выше величина микросечения поглощения активной зоны σa (а значит - и Σa), тем больше тепловых нейтронов поглощается при Е < Eнв, тем больше "выедание" левого крыла спектра, а это значит, что положение максимума спектра (характеризуемое Енв - наиболее вероятной энергией тепловых нейтронов) с увеличением поглощающей способности среды должно смещаться вправо, в область более высоких энергий. Иначе говоря, с увеличением поглощающих свойств среды энергетический спектр тепловых нейтронов ужестчается. Но, т.к. положение максимума в спектре тепловых нейтронов определяет температуру нейтронов Тн (ведь Енв= kTн), то можно выразиться иначе: с увеличением поглощающих свойств среды повышается температура нейтронов в ней. И чем больше величина макросечения поглощения среды (Σa) - тем больше величина температуры нейтронов в ней (Тн) отклоняется от её термодинамической температуры (Т) в сторону увеличения.

С другой стороны, чем выше величина замедляющей способности среды (ξΣs), тем с большей скоростью пополняется за счёт замедления нейтронов весь спектр тепловых нейтронов (в том числе и его левое крыло). Поэтому положение его максимума, наоборот, смещается влево, в область более низких энергий, т.е. с увеличением замедляющей способности среды спектр тепловых нейтронов «умягчается», и температура тепловых нейтронов в среде с лучшими замедляющими свойствами меньше отличается от термодинамической температуры этой среды по сравнению со средой с более слабыми замедляющими свойствами.

Таким образом получается, что температура нейтронов Тн находится в прямой зависимости от величины Σa среды активной зоны и в обратной зависимости - от ξΣs.

Это дало повод к предположению, что обе зависимости являются пропорциональными, что дает лёгкую возможность построить полуэмпирические зависимости для расчёта температуры нейтронов в тепловом реакторе:

Таким образом, температура нейтронов в тепловом реакторе - величина, прямо пропорциональная термодинамической температуре активной зоны и величине, обратной коэффициенту замедления среды в ней.

Приведённые формулы получены, строго говоря, для гомогенных смесей топлива и замедлителя, однако, с достаточной точностью могут служить и для оценки температуры нейтронов в гетерогенных активных зонах реакторов соответствующих типов, для чего в них должны подставляться средняя термодинамическая температура замедлителя Тз и величины гомогенизированных макросечений активной зоны Σa и Σs.

*) Гипотеза насчёт пропорциональности Тн,Тз и обратного коэффициента замедления являлась бы строго-доказательной только в том случае, если бы было строго доказано, что энергетический спектр тепловых нейтронов, как бы ни деформировала его среда своими поглощающими и замедляющими свойствами, всегда сохраняет максвелловскую форму.

Разговор был посвящен фермиевскому спектру замедляющихся нейтронов, но был смещен к спектру тепловых нейтронов, чтобы подчеркнуть два важных момента:

- Во-первых, между двумя этими энергетическими спектрами в критическом тепловом реакторе существует какая-то неясная пока взаимосвязь: любое, самое малейшее, изменение в спектре тепловых нейтронов обязательно должно повлечь за собой изменение и в спектре замедляющихся нейтронов, и, наоборот, изменение в фермиевском спектре должно отразиться и на максвелловском распределении тепловых нейтронов.

Эту взаимосвязь можно было бы предсказать и без углубленного экскурса в спектры, если просто (по-материалистически) уверовать в то, что всем поведением замедляющихся и тепловых нейтронов управляет одна Среда, только Среда и исключительно Среда. Это Она, благодаря присущим ей природным свойствам, единым образом, с единой закономерностью рождает с определённой скоростью быстрые нейтроны деления, замедляет их с определённой (связанной со скоростью генерации быстрых нейтронов) интенсивностью, поглощает их с определенной (связанной со скоростями генерации и замедления) скоростью, и определяет скорость утечки нейтронов из любого микрообъёма, - и все это природное предопределение свойственно нейтронам любой энергии. Иначе говоря, Среда, в силу своих природных свойств, и расставляет все нейтроны по энергиям в единый энергетический спектр, не являющийся ни спектром Уатта, ни спектром Ферми и ни спектром Максвелла.

- Во-вторых, хотя спектры Уатта, Ферми и Максвелла и отражают закономерности рождения, замедления и поглощения нейтронов, связать их в единое аналитическое выражение для единого энергетического спектра реактора не удаётся, так как спектры Уатта и Максвелла нормированы соответственно на один нейтрон деления и тепловой нейтрон, а спектр Ферми - вообще не является нормированным.

Не стоит воспринимать сказанное как критику существующей физической теории реакторов: скорее, это её очередная проблема, с которой любому человеку, связанному с ядерной энергетикой, следует быть знакомым. Потому, что её разрешение радикальным образом изменит не только систему теоретических представлений и облегчит их восприятие: должны открыться новые возможности для простых и быстрых инженерных расчётов и анализа эксплуатационной безопасности любых реакторов.

Пока же мы вынуждены довольствоваться упомянутой триадой энергетических спектров и для расчётов критических свойств реакторов пользоваться громоздкими (хотя и приближёнными) вычислениями с помощью ЭВМ.

5.7. Время замедления нейтронов в среде активной зоны

Если λs =1/Σs - средняя длина свободного пробега рассеяния нейтронов в среде, то за время dt нейтрон со скоростью v испытывает v dt/ λs = vΣsdt рассеяний.

С другой стороны, нейтрон за время dt замедляется в элементарном интервале энергий dE ниже энергии Е, и то же число рассеяний можно выразить как dE/ξE. Приравнивая эти величины, имеем:

Интегрируя последнее выражение в пределах от Ео до Ес, имеем:

Подсчёт по формуле (5.7.1) для трёх известных замедлителей тепловых реакторов даёт следующие результаты:

-для воды в нормальных условиях tз ≈ 1.7 .10-5 c;

-для графита (плотностью γ = 1.6 г/см3) tз ≈ 1.57 .10-4 c;

-для бериллия (плотностью γ = 1.85 г/см3) tз ≈ 77 .10-5 c.

О том, что время замедления - величина порядка нескольких стотысячных долей секунды, нам не раз придётся вспомнить при изучении раздела кинетики реактора.

Краткие выводы

На завуалированный в названии темы 5 вопрос: как процесс замедления нейтронов влияет на размножающие свойства реактора? - можно кратко ответить так:

а) замедление нейтронов в реакторе большей или меньшей своей интенсивностью воздействует на один из шести сомножителей эффективного коэффициента размножения - вероятность избежания утечки замедляющихся нейтронов (pз);

б) величина pз = exp(-B2τт) определяется двумя сложными параметрами - возраст тепловых нейтронов в реакторе τт и геометрический параметр реактора B2;

в) возраст тепловых нейтронов τт - комплексная характеристика замедляющих свойств среды активной зоны, отражающая её способность давать определённое среднеквадратичное пространственное смещение нейтронов в процессе их замедления - от точки рождения быстрого нейтрона до точки, где он снижает свою энергию до уровня энергии сшивки (т.е. становится тепловым); величина возраста тепловых нейтронов в каждом однородном материале в каждом определенном его термодинамическом состоянии - своя;

г) возраст тепловых нейтронов τт = ln (Eo/Ec)/3ξΣsΣtr, кроме замедляющей способности среды ξΣs, содержит величину Σtr - транспортного макросечения среды, представляющую собой величину макросечения рассеяния этой среды, скорректированную с учётом анизотропии рассеяния; поэтому и потребовалось вспомнить физическое понятие анизотропии рассеяния (неравновероятности рассеяния нейтронов ядрами по разным направлениям) и её меры - среднего косинуса угла рассеяния, величина которого определяется только массой ядер-рассеивателей (μ ≈ 2/3A);

д) величина возраста тепловых нейтронов зависит от температуры среды: в твёрдых веществах она слабо уменьшается за счёт температурного ужестчения спектра тепловых нейтронов и возрастания энергии сшивки; в жидкостях и газах - существенно увеличивается за счёт температурного уменьшения плотности этих сред; в реакторах с водой под давлением величина возраста тепловых нейтронов с увеличением средней температуры активной зоны также однозначно возрастает;

е) мы познакомились с уравнением возраста Ферми, решение которого позволяет теоретически найти пространственно-энергетическое распределение замедляющихся нейтронов в объёме активной зоны, а в практическом плане возрастного приближения - скорость генерации тепловых нейтронов в активной зоне теплового реактора;

ж) спектр замедляющихся нейтронов (спектр Ферми) показывает, что распределение замедляющихся нейтронов по энергиям подчинено закону nз(E) ~ E-3/2 для любых не поглощающих замедляющиеся нейтроны сред;

з) время замедления tз, составляющее часть времени жизни нейтронов, - величина порядка 10-5 с в чистых замедлителях и в активных зонах реальных реакторов.

Тема 6.

ДИФФУЗИЯ И РАЗМНОЖАЮЩИЕ СВОЙСТВА ТЕПЛОВОГО РЕАКТОРА

В полученной ранее формуле для величины эффективного коэффициента размножения в тепловом реакторе

kэ = η ε ϕ θ pз pт

есть сомножитель pт, который так же логически напрямую связан с процессом диффузии тепловых нейтронов в реакторе, как величина pз - с процессом замедления.

Вероятность избежания утечки тепловых нейтронов - это доля тепловых нейтронов, избежавших утечки из активной зоны в процессе диффузии, от общего числа генерируемых в активной зоне тепловых нейтронов поколения.

Диффузия тепловых нейтронов, как и замедление эпитепловых, - это процесс пространственного их перемещения в среде активной зоны реактора. Единственной разницей этих процессов является то, что при замедлении кинетическая энергия нейтронов быстро снижается за счёт рассеяний на ядрах среды, а при диффузии величина кинетической энергии тепловых нейтронов слабо колеблется от рассеяния к рассеянию около среднего значения. В силу того, что сами ядра среды в своем тепловом движении обладают различными кинетическими энергиями, величины которых колеблются около некоторого среднего значения, определяемого термодинамической температурой среды.

А раз так, то тепловым нейтронам в процессе диффузии так же свойственно испытывать утечку из объёма активной зоны, как и эпитепловым - в процессе замедления. Хотя - явно в меньшей степени: скорости движения тепловых нейтронов во много раз меньше скоростей замедляющихся нейтронов, а возможностей для взаимодействий с ядрами среды (в частности - для поглощений) у тепловых нейтронов существенно большие, чем у эпитепловых (у подавляющего большинства ядер микросечения поглощения тепловых нейтронов существенно большие, чем сечения поглощения нейтронов любых других энергий).

Как и у замедляющихся нейтронов, утечка из активной зоны тепловых нейтронов возможна не из любой точки ее объёма, а лишь из периферийного её слоя. Тепловые нейтроны, родившиеся в результате процесса замедления в пределах этого слоя, могут покинуть активную зону раньше, чем они будут поглощены, но рождённые в более глубоких слоях тепловые нейтроны - такой возможности лишены.

Аналогичные представления и сходство в рассуждениях о процессах замедления и диффузии приводят к одинаковому выводу, касающемуся величины вероятности избежания утечки тепловых нейтронов; поэтому нет нужды повторять рассуждения, уже приводимые в начале п.5.1 для pз; по аналогии запишем сразу для величины pт:

рт = f (геометрии а.з., каких-то диффузионных свойств среды а.з.)

И если аналогичную зависимость для величины pз в п.5. удалось расшифровать: pз = f(B2; τт), - то относительно зависимости величины pт от параметра реактора B2 мы пока можем говорить лишь предположительно, а что собой представляет характеристика диффузионных свойств среды активной зоны - пока неясно.

Но начнём всё-таки с неё. Интуиция подсказывает, что эта характеристика должна быть сходной по смыслу с возрастом тепловых нейтронов, то есть она должна отражать способность среды активной зоны давать определённое среднеквадратичное пространственное смещение тепловых нейтронов в процессе их диффузии в этой среде.

6.1.Закон диффузии тепловых нейтронов и длина диффузии

6.1.1.Нейтронный газ и его температура. Называть совокупность тепловых нейтронов в среде нейтронным газом имеются все формальные основания. Действительно, тепловые нейтроны по их свойствам близки к идеальному газу:

-из-за электронейтральности нейтроны не взаимодействуют друг с другом;

нейтронам принципиально чужды силы взаимодействия типа вандерваальсовых сил межмолекулярного сцепления в реальных газах, то есть сил электрической природы;

-нейтронный газ - пространственно очень разреженная совокупность частиц:

плотность нейтронов в самых энергонапряжённых реакторах по порядку величины не превышает 109 нейтр/см3, в то время как, скажем, молекулярная концентрация воды в разреженном перегретом паре составляет никак не меньше 1019 молекул/см3.

Близость свойств нейтронного газа к свойствам идеального газа даёт возможность описывать движение больших совокупностей свободных тепловых нейтронов в среде с использованием зависимостей молекулярной теории идеальных газов.

Скажем, абсолютная температура идеального газа Т - параметр его состояния, связанный с наиболее вероятной энергией молекул этого газа зависимостью Енв = kТ, где k = 8.62 .10-5 эВ/К - константа Больцмана. У тепловых нейтронов величина наиболее вероятной энергии

Енв = kTн

тоже связана с величиной температуры нейтронов пропорциональной связью с тем же коэффициентом пропорциональности k, но это не означает, что температуры среды и нейтронов - одна величина, хотя по определению тепловые нейтроны и находятся в кинетическом равновесии с ядрами среды, в которой они движутся. Положение максимума спектра тепловых нейтронов, как говорилось в п.5.6, определяется не только температурой, но и соотношением поглощающих и замедляющих свойств среды. Если бы среда не поглощала тепловые нейтроны, положения максимумов больцмановского спектра молекул и максвелловского спектра тепловых нейтронов, движущихся в этой среде, в точности совпадали бы, а, значит, совпадали бы и величины температур среды и нейтронов. Но идеальных, не поглощающих нейтроны, сред в природе нет, поэтому в реальных средах температура нейтронов Тн всегда выше, чем температура Т среды, где движутся тепловые нейтроны, и различие этих температур тем больше, чем меньше величина коэффициента замедления среды (см. формулу (5.6.4)).

6.1.2.Закон диффузии тепловых нейтронов. Из близости свойств нейтронного

иидеального газов следует, что описание интенсивности направленного переноса тепловых нейтронов в среде должно подчиняться закону газовой диффузии Фика, который, как оговорено в соответствующем разделе кинетической теории, в полной мере справедлив только для идеальных газов.

Газовая диффузия - процесс направленного переноса молекул газа, движущей силой которого является разница молекулярных концентраций газа в различных точках объёма среды. Перенос молекул направлен от зоны с большей концентрацией молекул к зоне с меньшей их концентрацией, и при длительном протекании в замкнутом объёме

он приводит к выравниванию концентраций по всему этому объёму. Так же обстоит дело и с тепловыми нейтронами, диффундирующими в среде. Разница в представлениях о газовой и нейтронной диффузии состоит только в том, что:

-при газовой диффузии молекулы сталкиваются и обмениваются кинетическими энергиями между собой непосредственно, а обмен кинетическими энергиями между тепловыми нейтронами происходит не в непосредственных столкновениях, а опосредствованно, то есть через посредство ядер среды, которые рассеивают их в процессе диффузии;

-при газовой диффузии газовые молекулы не исчезают, а при диффузии тепловых нейтронов в реальных средах происходит непрерывное их поглощение.

Применительно к диффузии тепловых нейтронов закон Фика записывают так:

В этом выражении:

R

I (r ) - вектор плотности тока диффузии тепловых нейтронов в точке среды с ко-

ординатами r (напомним: величина вектора I определяет интенсивность направленного перемещения нейтронов через единичную площадку, ориентированную перпендикулярно направлению этого вектора, за единицу времени, а сам вектор указывает направление их переноса);

Ñn(r ) - оператор Гамильтона функции n(r ) распределения плотности тепловых

нейтронов по координатам, иначе называемый в теории поля градиентом функции n в точке с координатами r . Градиент - тоже вектор, но его направление - направление

возрастания плотности нейтронов - противоположно направлению вектора I , поэтому в правой части (6.1.1) и стоит знак минус.

Скалярная величина градиента представляет собой сумму частных производных функции плотности нейтронов по координатам:

| grad n( r ) | = dn/dx + dn/dy + dn/dz,

так что в частном случае линейной диффузии, когда плотность нейтронов изменяется только вдоль одной координатной оси, величина градиента плотности нейтронов вырождается в обычную первую производную функции плотности по этой координате.

D* - коэффициент пропорциональности, называемый коэффициентом диффузии.

Так как вектор плотности тока I имеет скалярную размерность нейтр/см2с, а градиент плотности нейтронов - нейтр/см4, то размерность коэффициента диффузии D* - см2/с.

В теории реакторов в силу большего удобства закон Фика чаще записывают не через градиент плотности тепловых нейтронов, а через градиент плотности их потока (grad Ф). Формально умножив и разделив правую часть (6.1.1) на одну и ту же величину - среднюю скорость движения тепловых нейтронов (v), получим:

сохраняет смысл коэффициента диффузии, то есть плотности тока при единич-

ной величине градиента плотности потока тепловых нейтронов.

В кинетической теории нейтронов доказано, что величина этого коэффициента D определяется рассеивающими свойствами среды с учётом анизотропии рассеяния тепловых нейтронов на её ядрах, то есть:

Таким образом, в развёрнутом виде закон диффузии тепловых нейтронов:

6.1.3. Время диффузии тепловых нейтронов. Под временем диффузии tд пони-

мается среднее время от момента рождения теплового нейтрона до момента его поглощения.

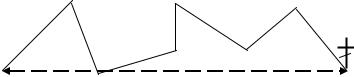
Путь теплового нейтрона от точки рождения до точки поглощения

Точка рождения ТН (точка, в которой замедляющийся нейтрон «пересёк» Ес )

В течение времени диффузии тепловой нейтрон в среде пробегает ломаный путь, равный среднему пробегу до поглощения в рассматриваемой среде λa = 1/Σa. А поскольку тепловой нейтрон проходит этот путь со средней скоростью v, время, за которое он его проходит:

Для получения представлений о порядке величины tд в различных средах подсчи-

таем её для для стандартных нейтронов (v = 2200 м/с).

Вводе при нормальных условиях (Σa » 0.02 см-1): tд = 1/(2.2 .105 .0.02) » 2.3 .10-4 c;

Вграфите (γ = 1.6 г/см3, Σa » 3 . 10-4см-1): tд = 1/(2.2 .105 . 3 .10-4) » 0.015 c;

Втопливной композиции UO2 плотностью γ = 10 г/см3 при обогащении x = 2% (Σa » 0.36 см-1) tд = 1/(2.2 .105 . 0.36) » 1.26 .10-5 c.

Как видим, время диффузии тепловых нейтронов - величина, значительно большая времени замедления их до теплового уровня в тех же средах (см.п.5.7). Чем больше поглощающих материалов присутствует в активной зоне теплового реактора, тем меньше величина времени диффузии тепловых нейтронов, а, значит, - меньше среднее

время жизни поколения нейтронов в реакторе.

6.1.4. Длина диффузии. Ранее вскользь отмечалось, что диффузионная характеристика среды активной зоны, определяющая величину вероятности избежания утечки тепловых нейтронов, должна быть связана со среднеквадратичным пространственным смещением тепловых нейтронов в процессе диффузии таким же образом, как возраст тепловых нейтронов связан со среднеквадратичной длиной замедления. К этому подталкивает почти полная аналогия представлений о процессах замедления и диффузии.

По определению кинетической теории нейтронов:

Квадрат длины диффузии тепловых нейтронов в среде - шестая часть среднего квадрата удаления теплового нейтрона в момент его поглощения от точки его рождения в этой среде.

И поскольку полученное в кинетической теории значение среднего квадрата пространственного смещения теплового нейтрона при диффузии:

___

lт2 = 2/Σa Σtr,

то величины квадрата и самой длины диффузии будут равны:

Как видим, квадрат длины диффузии L2 - такая же и по смыслу, и по размерно-

сти (см2) характеристика диффузионных свойств среды, какой является возраст теп-

ловых нейтронов τт - характеристика замедляющих свойств среды. Длина диффузии среды L (и её квадрат) характеризует её способность давать определённое среднеквадратичное пространственное смещение теплового нейтрона от точки рождения до точки его поглощения.

Поэтому каждому конкретному веществу в нормальных условиях (при t = 20оС или Т = 293К и нормальном атмосферном давлении) свойственна своя, стандартная длина диффузии, например:

-у воды (Н2О) Lo = 2.714 см;

-у графита (С) Lo = 51.2 см;

-у бериллия (Ве) Lo = 22.1 см;

-у оксида бериллия (ВеО) Lo = 30.0 см;

- у тяжёлой воды (D2O) Lo = 171 см и т.д.

Стандартные длины диффузии большинства материалов, используемых в реакторостроении, приводятся в справочниках по ядерным константам.

6.1.5. Зависимости длины диффузии веществ от температуры и давления. Так как величины макросечений поглощения и транспортного равны произведениям соответствующих микросечений на ядерную концентрацию:

Σa = σa N и Σtr = σtr N,

то выражение для квадрата длины диффузии однородного вещества можно представить в таком виде:

В правой части выражения (6.1.8а) влиянию температуры подвержены две величины - микросечения поглощения σ a и ядерной концентрации N.

Величина микросечения поглощения ядер любого вещества с ростом температуры

падает

так как с ростом температуры вещества приблизительно пропорционально величине температуры Т растёт и температура нейтронов Тн.

Ядерная концентрация жидкого или газообразного вещества с ростом температуры падает, твёрдого вещества - практически не изменяется.

Температурное уменьшение σa и N в соответствии с (6.1.8а) приводит к одно-

значному увеличению длины диффузии. Схематически это выглядит так: