2. Критерий Гурвица.

Параметр Гурвица возьмем равным γ=0,6: γ= min а_ij+(1-γ) max а_ij

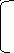
5 10 18 25 5 25 5*0,6+0,4*25=13

А = 8 7 8 23 7 23 7*0,6+0,4*23=13,4

21 18 12 21 12 18 12*0,6+0,4*18=14,4

20 22 19 15 15 22 15*0,6+0,4*22=17,8

Получаем H = max[0.6 min а_ij+(1-0.6) max а_ij]=17.8

^{i j}

Ответ: оптимальной стратегией первого игрока является

стратегия А₄.

3. Критерий Сэвиджа (критерий минимаксного риска).

Необходимо построить матрицу рисков.

Для этого:

1) вычислить максимальные значения по столбцам

5 10 18 25

А = 8 7 8 23

21 18 12 21

20 22 19 15

21 22 19 25

2) вычислить матрицу рисков: r_ij= max а_ij- а_ij

21-5 22-10 19-18 25-25 16 12 1 0

r_ij= 21-8 22-7 19-8 25-23 = 13 15 11 2

21-21 22-18 19-12 25-21 0 4 7 4

21-20 22-22 19-19 25-15 1 0 0 10

3) вычислить максимальные значения по строкам и из них выберем строку с минимальным значением:

16 12 1 0 16

13 15 11 2 15

r_ij= 0 4 7 4 7

1 0 0 10 10

Получаем H = min max r_ij = 7 при применении стратегии А₃.

^{i j}

Ответ: оптимальной стратегией первого игрока является

стратегия А₃.

4. Критерий Лапласа. N

Вычислить средние арифметические по строкам [1/n ∑ а_ij]

5 10 18 25 0.25 (5+10+18+25)=14.5 ^j=1

A = 8 7 8 23 0.25 (8+7+8+23)=11.5

21 18 12 21 0.25 (21+18+12+21)=18

20 22 19 15 0.25 (20+22+19+15)=19

_n

Получаем H = max [1/n ∑ а_ij] =19 при применении стратегии А₄.

^{i j=1}

Ответ: оптимальной стратегией первого игрока является

стратегия А₄.

Выбор стратегии в условиях риска (при наличии вероятностной информации).

В₁ В₂ В₃ В_{4 n}

А₁ 5 10 18 25 H = max∑P_j а_ij

А₂ 8 7 8 23 ^{i j=1}

А₃ 21 18 12 21

А₄ 20 22 19 15

Вероятности стратегий второго игрока.

В1	В2	В3	В4
0.2	0.15	0.35	0.3

5*0.2+10*0.15+18*0.35+25*0.3=16.30

8*0.2+7*0.15+8*0.35+23*0.3=12.35

21*0.2+18*0.15+12*0.35+21*0.3=17.40

20*0.2+22*0.15+19*0.35+15*0.3=18.45

Получаем Н = 18,45 при применении стратегии А₄.

Ответ: оптимальной стратегией первого игрока является

стратегия А₄.

ПРИМЕР №2

Предприятие имеет возможность самостоятельно планировать объемы выпуска сезонной продукции А₁, А₂, А₃. Не проданная в течении сезона продукция позже реализуется по сниженной цене. Данные о себестоимости продукции, отпускных ценах и объемах реализации в зависимости от уровня спроса приведены в таблице:

Вид продукции	Себесто-имость	Цена единицы Продукции		Объем реализации При уровне спроса
		В течение сезона	После уценки	Повы-шенном	среднем	Пони- женном
А1	d1	р1	q1	a1	b1	c1
А2	d2	р2	q2	a2	b2	c2
А3	d3	р3	q3	а3	b3	c3

Требуется:

1) придать описанной ситуации игровую схему, указать допустимые стратегии сторон, составить платежную матрицу

2) дать рекомендации об объемах выпуска продукции по видам, обеспечивающих предприятию наивысшую прибыль.

Указание. Для уменьшения размерности платежной матрицы считать, что одновременно на все три вида продукции уровень спроса одинаков:

повышенный, средний или пониженный.

Вид продукции	Себесто-имость	Цена единицы Продукции		Объем реализации При уровне спроса
		В течение сезона	После уценки	Повы-шенном	среднем	Пони- женном
А1	2,6	3,4	2,8	14	8	5
А2	3,7	4,2	3,2	38	22	9
А3	1,5	2,8	1,7	24	13	7

Решение.

В игре участвуют 2 игрока: А - производитель, В - потребитель.

Игрок А стремится реализовать свою продукцию так, чтобы получить максимальную прибыль. Стратегиями игрока А являются:

А₁ - продавать продукцию при повышенном состоянии спроса

А₂ - продавать продукцию при среднем состоянии спроса

А₃ - продавать продукцию при пониженном состоянии спроса

Игрок В стремится приобрести продукцию с минимальными затратами. Стратегиями игрока В являются:

В₁ - покупать продукцию при повышенном состоянии спроса

В₂ - покупать продукцию при среднем состоянии спроса

В₃ - покупать продукцию при пониженном состоянии спроса

Интересы игроков А и В - противоположны. Определим цену продукции в течение сезона и после уценки:

Вид продукции	себестоимость	Цена в течение сезона	Цена после уценки
А1	2,6	3,4-2,6=0,2	2,8-2,6=0,2
А2	3,7	4,2-3,7=0,5	3,2-3,7= -5
А3	1,5	2,8-1,5=1,3	1,7-1,5=0,2

Рассчитаем элементы платежной матрицы

Предложение	Спрос
	стратегии	Повышенный спрос 14+38+24	Средний спрос 8+22+13	Пониженный спрос 5+9+7
	Повышенный спрос 14+38+24	14*0,8+38*0,5+ 24*1,3=61,4	8*0,8+(14-8) *0,2+ 22*0,5+(38-22)*(-5) +13*1,3+(24-13)*0,2 =29,7	5*0,8+(14-5)*0,2+ 9*0,5+(38-9)*(-5)+ 7*1,3+(24-7)=8,3
	Средний спрос 8+22+13	8*0,8+22*0,5+ 13*1,3=34,3	8*0,8+22*0,5+ 13*1,3=34,3	5*0,8+(8-5)*0,2+ 9*0,5+(22-9)*(-5)+ 7*1,3+(13-7)*0,2 =12,9
	Пониженный спрос 5+9+7	5*0,8+9*0,5+7*1,3 =17,6	5*0,8+9*0,5+ 7*1,3=17,6	5*0,8+9*0,5+ 7*1,3=17,6

Платежная матрица примет вид

Стратегии	В1	В2	В3	αi=min аij j
А1	61.4	29.7	8.3	8.3
А2	34.3	34.3	12.9	12.9
А3	17.6	17.6	17.6	17.6
βj=max аij i	61.4	34.3	17.6

α = max α_i = 17.6 β = min β_j = 17.6

Так как α = β = ν = 17,6, то найдена седловая точка. Значит оптимальное решение: А₃; В₃

Производитель (игрок А) получит гарантированную прибыль в размере 17,6 ден.ед., если будет реализовывать свою продукцию при пониженном уровне спроса в объеме 5,9 и 7 ед. соответственно продукции А₁, А₂ и А₃

Контрольные вопросы:

1.Дайте определение конфликтной ситуации.

2.Как называется математическая модель конфликтной ситуации?

3.Как называются заинтересованные стороны в теории игр?

4.Какая игра называется антагонистической? Приведите пример.

5.Дайте определение понятию «стратегия».

6.Что понимается под исходом конфликта?

7.Дайте определение понятию «выигрыш».

8.На какие классы делятся игры в зависимости от числа игроков?

9.В чем состоит цель игрока А при выборе стратегии ?

10. В чем состоит суть максиминного принципа оптимальности и как называется выигрыш, полученный в соответствии в этим принципом?

11.Почему максимин α называют нижней ценой игры?

12.В чем состоит цель игрока В при выборе стратегии?

13.Почему минимакс β называют верхней ценой игры?

14.Почему справедливо неравенство α < β ?

15.Дайте определение цены игры в чистых стратегиях.

16.Какая игра называется игрой в смешанных стратегиях?

17.Как найти оптимальную смешанную стратегию игрока А и цену игры 2 х n геометрически?

18.Что в теории игр понимается под термином «природа»?

19.Приведите примеры в которых решение принимается в условиях неопределенности, связанной с неосознанным принятием различных факторов.

20.Чем отличается выбор оптимальных стратегий игроков в играх с природой от антагонистических игр?

21.Что понимается под риском игрока в игре с природой, и каким образом формируется матрица рисков,

22.Дайте определение критерия Вальда и как по нему определяется выигрыш?

23. Дайте определение критерия Севиджа и как по нему определяется выигрыш?

24. Дайте определение критерия Лапласа и как по нему определяется выигрыш?

25. Дайте определение критерия Байеса и как по нему определяется выигрыш?

26. Какой принцип выбора оптимальной стратегии лежит в основе критерия пессимизма –оптимизма Гурвица относительно выигрышей?