§ 16.4 Энергия магнитного поля

Если в контуре с индуктивностью L течёт ток I, то в момент размыкания цепи возникает индукционный ток и им совершается работа. Эта работа совершается за счёт энергии исчезнувшего при размыкании цепи магнитного поля. На основании закона сохранения и превращения энергию магнитного поля превращается главным образом в энергию электрического поля, за счёт которой происходит нагревание проводников. Работа может быть определена из соотношения

dA=ε_смIdt

Так как , то

dA=-LIdI

Уменьшение энергии магнитного поля равно работе тока, поэтому

(16.18)

Формула справедлива для любого контура и показывает, что энергия магнитного поля зависит от индуктивности контура и силы тока, протекающего по нему.

Рассчитаем энергию однородного магнитного поля длинного соленоида, индуктивность которого определяется по формуле L = μμ₀n²V. B этом случае формула энергии примет вид

Учитывая, что напряжённость поля внутри бесконечно длинного соленоида Н=In, получаем

(16.19)

Выразим энергию через индукцию магнитного поля B= μμ₀H:

(16.20)

Или

(16.21)

Вследствие того, что магнитное поле соленоида однородно и локализовано внутри соленоида, энергия распределена по объёму соленоида с постоянной плотностью

(16.22)

Учитывая последние три формулы, получаем

Учитывая правило Ленца, можно заметить, что явление самоиндукции аналогично проявлению инертности тел в механике. Так, вследствие инертности тело не мгновенно приобретает определённую скорость, а постепенно. Так же постепенно происходит и его торможение. То же самое, как мы видели, происходит и с силой тока при самоиндукции. Эту аналогию можно провести и дальше.

и

эти уравнения эквивалентны.

т.е. m ~L , υ~I

Эквивалентны и формулы

Примеры решения задач

Пример. В магнитном поле, изменяющемся по закону B=B₀cosωt (B₀=5мТл,

ω=5с^-1), помещён круговой проволочный виток радиусом r=30см, причём нормаль к витку образует с направлением поля угол α=30º. Определите ЭДС индукции, возникающую в витке в момент времени t=10с.

Дано: B=B₀cosωt; B₀=5мТл=5∙10^-3 Тл; ω=5с^-1; r=30см=0,3 м; α=30º; t=10 с.

Найти: ε_i.

Решение: Согласно закону Фарадея,

, (1)

Где магнитный поток, сцепленный с витком при произвольном его расположении относительно магнитного поля.

Ф=BScosα.

По условию задачи B=B₀cosωt, а площадь кольца S=πr², поэтому

Ф=πr² B₀cosωt∙cosα. (2)

Подставив выражение (2) в формулу (1) и продифференцировав, получаем искомую ЭДС индукции в заданный момент времени:

Ответ: ε_i=4,69 мВ.

Пример В соленоиде длиной ℓ=50см и диаметром d=6см сила тока равномерно увеличивается на 0,3А за одну секунду. Определите число витков соленоида, если сила индукционного тока в кольце радиусом 3,1 см из медной проволоки (ρ=17нОм∙м), надетом на катушку, I_к=0,3 А.

Дано: ℓ=50см=0,5 м; d=6см=0,06м; ;r_к=3,1см=3.1∙10^-2м; ρ=17нОм∙м=17∙10^-9 Ом∙м; I_к=0,3 А.

Найти: N.

Решение. При изменении силы тока в соленоиде возникает ЭДС самоиндукции

(1)

где - индуктивность соленоида. Подставив это выражение в (1)

с учётом

.

ЭДС индукции, возникающая в одном кольце, в N раз меньше, чем найденное значение ЭДС самоиндукции в соленоиде, состоящем из N витков, т.е.

. (2)

Согласно закону Ома, сила индукционного тока в кольце

, (3)

где - сопротивление кольца. Поскольку ℓ_к=πd, а S_к=πr_к², выражение (3) примет вид

Подставив в эту формулу выражение (2), найдём искомое число витков соленоид

.

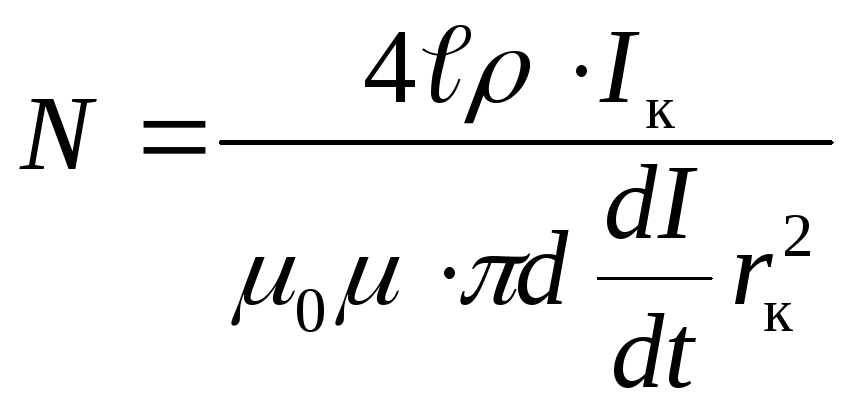Ответ: N=150

Пример В однородном магнитном поле подвижная сторона (её длина ℓ=20см) прямоугольной рамки (см. рисунок) перемещается перпендикулярно линиям магнитной индукции со скоростью υ=5 м/с. Определите индукцию В магнитного поля, если возникающая в рамке ЭДС индукции ε_i=0,2 В.

Дано: ℓ=20см=0,2 м; υ=5 м/с; ε_i=0,2 В.

Найти: B.

Р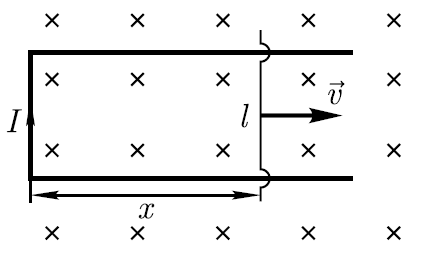ешение. При движении в магнитном поле подвижной стороны рамки поток Ф вектора магнитной индукции сквозь рамку возрастает, что, согласно закону Фарадея,

, (1)

приводит к возникновению ЭДС индукции.

Поток вектора магнитной индукции, сцепленный с рамкой,

Ф=Bℓx. (2)

Подставив выражение (2) в формулу (1) и учитывая, что B и ℓ - величины постоянные, получаем

откуда искомая индукция магнитного поля

Ответ: В=0,2 Тл.

Пример В однородном магнитном поле с индукцией В=0,2 Тл равномерно вращается катушка, содержащая N=600 витков, с частотой n=6 с^-1. Площадь S поперечного сечения катушка 100см². Ось вращения перпендикулярна оси катушки и направлению магнитного поля. Определите максимальную ЭДС индукции вращающейся катушки.

Дано: В=0,2 Тл; N=600; n=6 с^-1; S=100см²=10^-2 м².

Найти: (ε_i)_max.

Решение. Согласно закону Фарадея,

где Ф – полный магнитный поток, сцеплённый со всеми витками катушки. При произвольном расположении катушки относительно магнитного поля

Ф=NBScosωt, (1)

где круговая частота ω=2πn. Подставив ω в (1), получим

Ф=NBScos2πnt.

Тогда

ε_i=-NBS2πn(-sin2πnt)=2πnNBSsin2πnt,

ε_i=( ε_i)_max при sin2πnt=1, поэтому

(ε_i)_max=2πnNBS

Ответ: (ε_i)_max=45,2 В.

Пример Однослойная длинная катушка содержит N=300 витков, плотно прилегающих друг к другу. Определите индуктивность катушки, если диаметр проволоки d=0,7 мм (изоляция ничтожной толщины) и она намотана на картонный цилиндр радиусом r=1 см. .

Дано: N=300; d=0,7 мм=7∙10^-4 м; r=1 см=10^-2 м.

Найти: L.

Решение. Индуктивность катушки

(1)

где Ф – полный магнитный поток, сцепленный со всеми витками катушки; I - сила тока в катушке.

Учитывая, что полный магнитный поток

Ф=NBS

(N-число витков катушки; В – магнитная индукция; S – площадь поперечного сечения катушки); магнитная индукция в катушке без сердечника

(μ₀ – магнитная постоянная; ℓ- длина катушки), длина катушки

ℓ=Nd

(d-диаметр проволоки; витки вплотную прилегают друг к другу), площадь поперечного сечения катушки

S=πr²,

Получим осле подстановки записанных выражений в формулу (1) искомую индуктивность катушки:

Ответ: L=1,69 мГн.

Пример Первичная обмотка понижающего трансформатора с коэффициентом трансформации k=0,1 включена в сеть с источником переменного напряжения с ЭДС ε₁=220 В. Пренебрегая потерями энергии в первичной обмотке, определите напряжение U₂ на зажимах вторичной обмотки, если её сопротивление R₂=5 Ом и сила тока в ней I₂=2А.

Дано: k=0,1; ε₁=220 В; R₂=5 Ом; I₂=2А.

Найти: U₂.

Решение. В первичной обмотке под действием переменной ЭДС ε₁ возникает переменный ток I₁, создающий в сердечнике трансформатора переменногый магнитный поток Ф, который пронизывает вторичную обмотку. Согласно закону Ома, для первичной обмотки

где R₁ – сопротивление первичной обмотки. Падение напряжения I₁R₁ при быстропеременных полях мало по сравнению с ε₁ и ε₂. Тогда можем записать:

(1)

ЭДС взаимной индукции, возникающая во вторичной обмотке,

(2)

Из выражений (1) и (2) получаем

,

где - коэффициент трансформации, а знак «-» показывает, что ЭДС в первичной и вторичной обмотках противоположны по фазе. Следовательно, ЭДС во вторичной обмотке

ε₂=k ε₂.

Напряжение на зажимах вторичной обмотки

U₂= ε₂-I₂R₂= kε₁-I₂R₂.

Ответ: U₂=12 В.

Пример Соленоид без сердечника с однослойной обмоткой из проволоки диаметром d=0,4 мм имеет длину ℓ=0.5 м и поперечное сечение S=60см². За какое время при напряжении U=10 В и силе тока I=1,5 А в обмотке выделится количество теплоты, равное энергии поля внутри соленоида? Поле считать однородным.

Дано: d=0,4 мм=0,4∙10^-4 м; ℓ=0,5 м; S=60см²=6∙10^-3 м²; I=1,5А; U=10В; Q=W.

Найти: t.

Решение. При прохождении тока I при напряжении U в обмотке за время t выделяется теплота

Q=IUt. (1)

Энергия поля внутри соленоида

(2)

где (N – общее число витков соленоида). Если витки вплотную прилегают друг к другу, то ℓ=Nd, откуда . Подставив выражение для В иN в (2), получаем

. (3)

Согласно условию задачи, Q=W. Приравняв выражение (1) и (3),найдём искомое время:

Ответ: t =1,77 мс.

Пример Катушка без сердечника длиной ℓ=50 см содержит N=200 витков. По катушке течёт ток I=1А. Определите объёмную плотность энергии магнитного поля внутри катушки..

Дано: ℓ=50 см=0,5 м; N=200; I=1 А.

Найти: ω.

Решение. Объёмная плотность энергии магнитного поля (энергия единицы объёма)

, (1)

где - энергия магнитного поля (L - индуктивность катушки); V=Sℓ- объём катушки (S - площадь катушки; ℓ- длина катушки).

Магнитная индукция поля внутри соленоида с сердечником с магнитной проницаемостью μ равна

.

Полный магнитный поток, сцепленный со всеми витками соленоида,

.

Учитывая, что Ф=LI, получаем формулу для индуктивности соленоида:

(2)

Подставив выражение (2) в формулу (1) с учётом того, что , найдём искомую объёмную плотность энергии магнитного поля внутри катушки:

Ответ: ω=0,1 Дж/м³.