
Билет 1







Пример.
Исследовать
на линейную зависимость такие функции:
![]() .
.
Решение
Исследование
проведем в интервале
![]() ,
который представляет собой
,
который представляет собой
область определения заданных функций. Применим правило для определения
линейной зависимости двух функций, указанное в начале страницы. Так как при
![]() имеем:
имеем:
![]() ,
то данные функции линейно независимы
на
,
то данные функции линейно независимы
на![]() .
.
Билет 2

Основные
свойства неопределенного интеграла
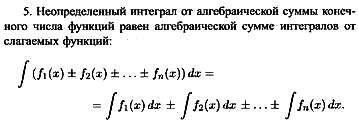



Билет 3
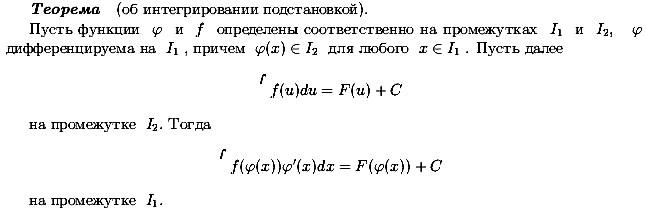
![]()
![]()
![]()

![]()

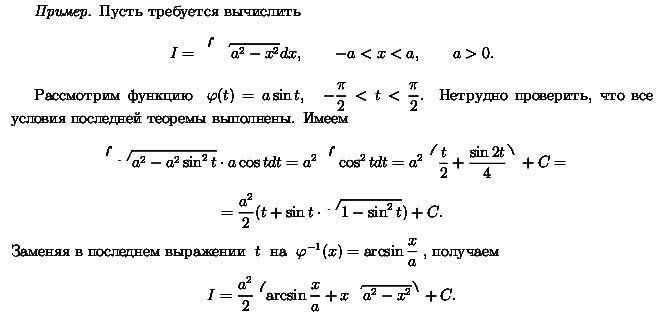


Билет 4

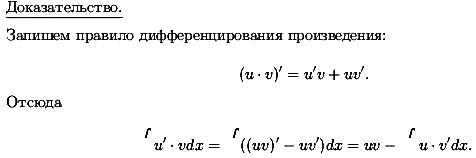



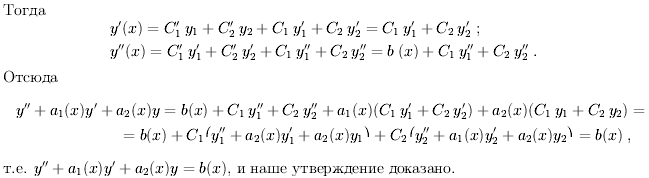
Билет 5



![]()




Билет 6
Дробно-рациональная
функция
![]() называется
правильной,
называется
правильной,
если степень многочлена, стоящего в числителе, ниже степени
многочлена в знаменателе, и неправильной в противном случае.
Алгоритм:
1.Если дробь неправильная — выделить целую часть. Получим
интеграл от целой части (интегрируется непосредственно) и
интеграл от правильной дроби;
2.Если числитель равен дифференциалу знаменателя (или
отличается от него постоянным множителем), то использовать
замену переменной z=знаменатель;
3.Если числитель равен дифференциалу некого многочлена (или
отличается от него постоянным множителем), а знаменатель равен
степени того же многочлена, то использовать замену переменной
z=знаменатель;
4.В остальных случаях нужно разложить дробь на сумму простейших.
Пример
![]() .
.![]() =
=![]() ;
;
![]() =
=![]()

![]()
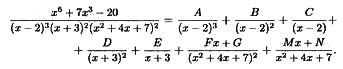
Общим решением дифференциального уравнения
F(x, y(x), y '(x), y ''(x), … , y(n )(x)) = 0
называется функция
y = Ф(x, С1, С2, … , Сn),
содержащая некоторые постоянные (параметры) С1, С2, … , Сn, и обладающая следующими свойствами:
Ф(x, С1, С2, … , Сn) является решением уравнения при любых допустимых значениях С1, С2, … , Сm;
для любых начальных данных y(x0) = y0, y '(x0) = y1, y ''(x0) = y2, … , y(n − 1)(x0) = yn − 1, для которых задача Коши имеет единственное решение,
существуют значения постоянных С1 = A1, С2 = A2, … , Сn = An, такие что решение y = Ф(x, A1, A2, …, An) удовлетворяет заданным начальным условиям.
теорема о структуре общего решения линейного однородного уравнения).
Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y1(x), y2(x),..., yn(x) образуют фундаментальную систему решений этого уравнения, то общее решение уравнения имеет вид
y(x,C1,..., Cn) = C1y1(x) + C2y2(x) + ... + Cnyn(x),
где C1,...,Cn — произвольные постоянные.
Теорема.
Если
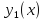 и
и
 – линейно независимые решения уравнения
– линейно независимые решения уравнения
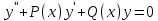 ,
то их линейная комбинация
,
то их линейная комбинация
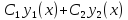 ,
где
,
где
 и
и
 –
произвольные постоянные, будет общим
решением этого уравнения.
–
произвольные постоянные, будет общим
решением этого уравнения.
Доказательство.
То,
что
 есть
решение уравнения (2.3), следует из теоремы
о свойствах решений лоду 2-го порядка.
Надо только еще показать, что решение
есть
решение уравнения (2.3), следует из теоремы
о свойствах решений лоду 2-го порядка.
Надо только еще показать, что решение
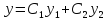 будет общим,
т.е. надо показать, что при любых начальных
условиях
будет общим,
т.е. надо показать, что при любых начальных
условиях
 ,
,
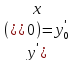 можно выбрать произвольные постоянные
можно выбрать произвольные постоянные
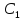 и
и
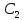 так,
чтобы удовлетворить этим условиям.
Запишем начальные условия в виде:
так,
чтобы удовлетворить этим условиям.
Запишем начальные условия в виде:
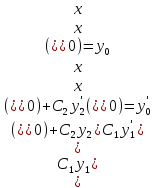
Постоянные
 и
и
 из
этой системы линейных алгебраических
уравнений определяются однозначно,
так как определитель этой системы
из
этой системы линейных алгебраических
уравнений определяются однозначно,
так как определитель этой системы
 есть значение определителя Вронского
для линейно независимых решений лоду
при
есть значение определителя Вронского
для линейно независимых решений лоду
при
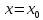 :
:
 ,
,
а такой определитель, как мы видели в предыдущем параграфе, отличен от нуля.
Билет 7

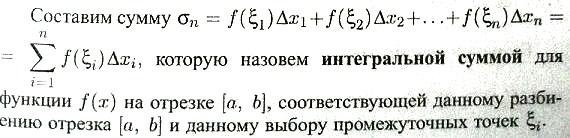

![]()

Общее
решение (8) на отрезке
 с непрерывными на этом отрезке
коэффициентами
с непрерывными на этом отрезке
коэффициентами
 и правыми частями
и правыми частями
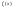 равно сумме общего решения соответствующей
однородной системы (9) и частного
решения
равно сумме общего решения соответствующей
однородной системы (9) и частного
решения
 неоднородной
системы (8).(
неоднородной
системы (8).(
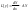 ,
тогда (6) можно переписать в виде:
,
тогда (6) можно переписать в виде:
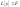 ,(8)
если
,(8)
если
 то
то
 (9))
(9))
Рассмотрим линейную однородную систему обыкновенных дифференциальных уравнений вида
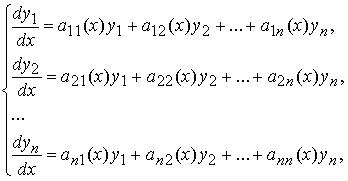
которая в векторной форме записывается в виде
![]() Здесь
Здесь
![]()
Матрица Φ, столбцами которой являются nлинейно независимых на [a, b] решений Y1(x), Y2(x), ..., Yn(x) однородной линейной системы Y' = A(x)Y называется фундаментальной матрицей решений системы:
![]()
Фундаментальная матрица решений однородной линейной системы Y' = A(x)Y удовлетворяет матричному уравнению Φ' = A(x)Φ.
Здесь
![]()
--------------- Квадратная матрица Φ(t), столбцы которой образованы линейно независимыми решениями x1(t), x2(t), ..., xn(t), называется фундаментальной матрицей системы уравнений. Она имеет следующий вид:
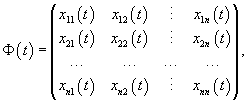
где xij (t) − координаты линейно независимых векторных решений x1(t), x2(t), ..., xn(t). Заметим, что фундаментальная матрица Φ(t) является невырожденной, т.е. для нее всегда существует обратная матрица Φ −1(t). Поскольку фундаментальная матрица содержит n линейно независимых решений, то при ее подстановке в однородную систему уравнений получаем тождество
![]()
Умножим это уравнение справа на обратную функцию Φ −1(t):
![]()
Полученное соотношение однозначно определяет однородную систему уравнений, если задана фундаментальная матрица. Общее решение однородной системы выражается через фундаментальную матрицу в виде
![]()
где C − n-мерный вектор, состоящий из произвольных чисел.------


![]()
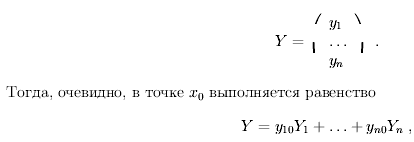

Билет 8
Если функция интегрируема по Риману на отрезке, то она ограничена
на этом отрезке. Зам.: условие ограниченности является необходимым
условием интегрируемости функции по Риману на отрезке.
Док-во:Пусть функция f(x) интегрируема на
[a,
b], тогда
![]() .
По определению интеграла
.
По определению интеграла
![]() ,
то есть
,
то есть
для
![]() и
любого набора точек
и
любого набора точек
![]() выполняется:
выполняется:
![]() ,
отсюда получаем:
,
отсюда получаем:![]()
Допустим, что функция не ограничена на [a, b], то есть не ограничена
на
некотором
![]() .
Обозначим остальную, не относящуюся к
.
Обозначим остальную, не относящуюся к
данному отрезку часть суммы за σ:
![]() ,
,
![]() В
силу неограниченности всегда можно
выбрать такое ξ*,
что
В
силу неограниченности всегда можно
выбрать такое ξ*,
что
![]() .Получено
противоречие,
.Получено
противоречие,
следовательно интегрируемая функция должна быть ограниченной



![]()



Билет 9
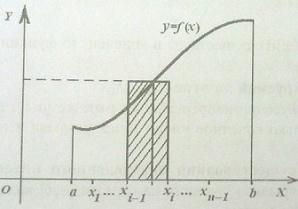
Если существует конечный предел I интегральной суммы при λ → 0, и он не зависит от способа выбора точек ξ i, способа разбиения отрезка, то этот предел называется определенным интегралом от функции f (x)по отрезку [a, b] и обозначается следующим образом:
![]()
![]()
![]()
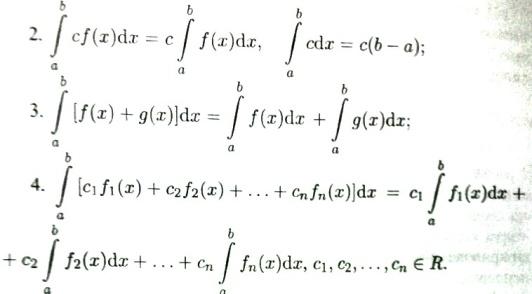
![]()

![]()
![]()

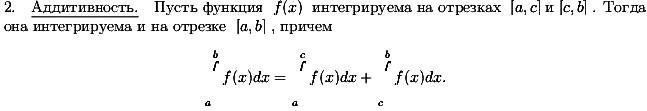

![]()

Общее
решение (8) на отрезке
 с непрерывными на этом отрезке
коэффициентами
с непрерывными на этом отрезке
коэффициентами
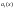 и правыми частями
и правыми частями
 равно сумме общего решения соответствующей
однородной системы (9) и частного
решения
равно сумме общего решения соответствующей
однородной системы (9) и частного
решения
 неоднородной
системы (8).(
неоднородной
системы (8).(
 ,
тогда (6) можно переписать в виде:
,
тогда (6) можно переписать в виде:
 ,(8)
если
,(8)
если
 то
то
 (9))
(9))
Рассмотрим линейную однородную систему обыкновенных дифференциальных уравнений вида

которая в векторной форме записывается в виде
![]() Здесь
Здесь
![]()
Матрица Φ, столбцами которой являются nлинейно независимых на [a, b] решений Y1(x), Y2(x), ..., Yn(x) однородной линейной системы Y' = A(x)Y называется фундаментальной матрицей решений системы:

Фундаментальная матрица решений однородной линейной системы Y' = A(x)Y удовлетворяет матричному уравнению Φ' = A(x)Φ.
Здесь
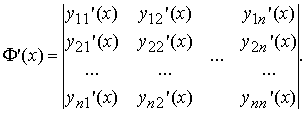
--------------- Квадратная матрица Φ(t), столбцы которой образованы линейно независимыми решениями x1(t), x2(t), ..., xn(t), называется фундаментальной матрицей системы уравнений. Она имеет следующий вид:

где xij (t) − координаты линейно независимых векторных решений x1(t), x2(t), ..., xn(t). Заметим, что фундаментальная матрица Φ(t) является невырожденной, т.е. для нее всегда существует обратная матрица Φ −1(t). Поскольку фундаментальная матрица содержит n линейно независимых решений, то при ее подстановке в однородную систему уравнений получаем тождество
![]()
Умножим это уравнение справа на обратную функцию Φ −1(t):
![]()
Полученное соотношение однозначно определяет однородную систему уравнений, если задана фундаментальная матрица. Общее решение однородной системы выражается через фундаментальную матрицу в виде
![]()
где C − n-мерный вектор, состоящий из произвольных чисел.
Билет 10

Теорема об оценке
интеграла.
Если на отрезке [a,b]
функция удовлетворяет неравенству
![]() ,
то
,
то
![]() .
Док-во.
Докажем левое неравенство (цифрами над
знаками импликации обозначены номера
применяемых ранее доказанных свойств):
.
Док-во.
Докажем левое неравенство (цифрами над
знаками импликации обозначены номера
применяемых ранее доказанных свойств):
![]() .
Аналогично доказывается и правое
неравенство.
.
Аналогично доказывается и правое
неравенство.
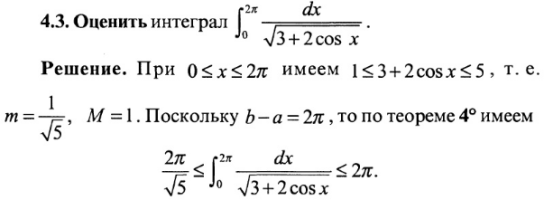

![]()

Билет 11

![]()
![]()
![]()
![]() или
или
![]()
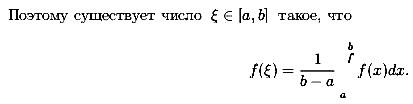
![]()
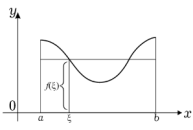

![]()
![]()
Общее
решение (8) на отрезке
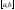 с непрерывными на этом отрезке
коэффициентами
с непрерывными на этом отрезке
коэффициентами
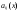 и правыми частями
и правыми частями
 равно сумме общего решения соответствующей
однородной системы (9) и частного
решения
равно сумме общего решения соответствующей
однородной системы (9) и частного
решения
 неоднородной
системы (8).(
неоднородной
системы (8).(
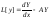 ,
тогда (6) можно переписать в виде:
,
тогда (6) можно переписать в виде:
 ,(8)
если
,(8)
если
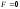 то
то
 (9))
(9))



Билет 12
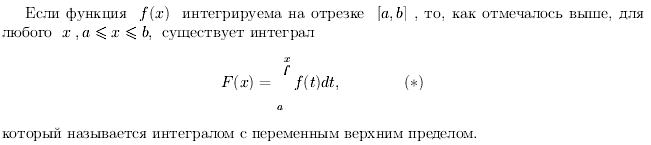


![]()
![]()
![]()
Ф-ла Ньютона-Лейбница

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


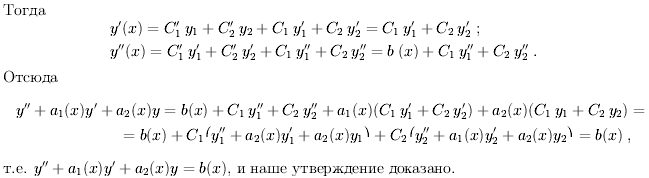
Билет 13

![]()
![]()

![]()
![]()
![]()

![]()
![]()
![]()





Билет 14

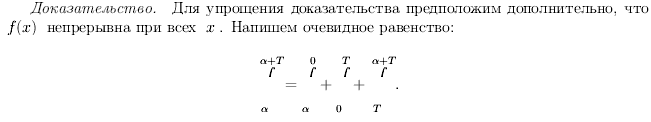

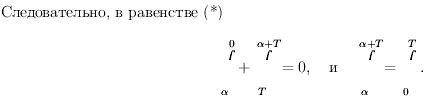

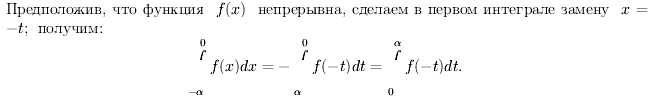
![]()
![]()
![]()
![]()



Билет 15

![]()

![]()


![]()
![]()
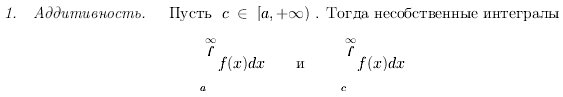
![]()
![]()
![]()
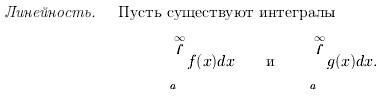
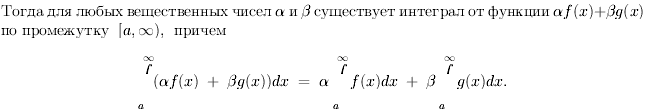




Билет 16
Пустьf(x)
определена на (a,b],
терпит бесконечный разрыв в точке x=a и
![]() .
Тогда:
.
Тогда:
Если
![]() ,
то используется обозначение
,
то используется обозначение
![]() и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
Если
![]() или
или
![]() ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а
![]() называется
расходящимся.
называется
расходящимся.
Пусть
f(x)
определена на (a,b],
терпит бесконечный разрыв при x=b и
![]() .
Тогда:
.
Тогда:
Если
![]() ,
то используется обознач….
Если
функция f(x)
терпит
разрыв во внутренней точке c
отрезка
,
то используется обознач….
Если
функция f(x)
терпит
разрыв во внутренней точке c
отрезка
![]() ,
то несобственный интеграл второго рода
определяется формулой:
,
то несобственный интеграл второго рода
определяется формулой:
![]()
![]()
Свойства.
1)
Если интеграл
![]() сходиться,
С – некоторое число, то интеграл
сходиться,
С – некоторое число, то интеграл
![]() также
сходиться и
также
сходиться и
![]()
2)
Если интегралы
![]() и
и
![]() сходятся,
то интеграл
сходятся,
то интеграл
![]() только
сходится и
только
сходится и
![]()
3)
Если функции
![]() и
и
![]() интегрируемы
при
интегрируемы
при![]() ,
то
,
то
![]()
4)
Пусть функция f(x) непрерывна
при x>=a
, функция
![]() определена,
непрерывна и имеет непрерывную
производную на промежутке
определена,
непрерывна и имеет непрерывную
производную на промежутке
![]() конечном
или бесконечном, где
конечном
или бесконечном, где
![]() <
<![]()
Тогда
![]()



 Билет
17
Билет
17

Д-во
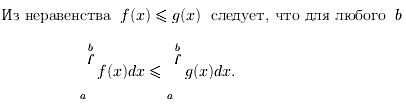

![]()



Билет 18

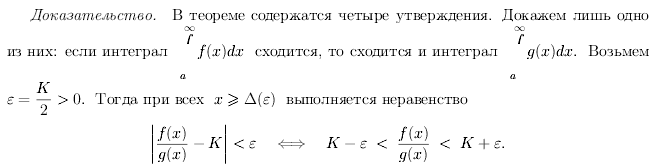

![]()
![]()
Пример.
![]()

Обыкновенное
дифференциальное уравнение 1-го порядка
(n=1)
имеет вид:
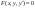 или, если его удается разрешить
относительно производной:
или, если его удается разрешить
относительно производной:
 .
Общее
решениеy=y(x,С)
или общий
интеграл
.
Общее
решениеy=y(x,С)
или общий
интеграл
 уравнения 1-го порядка содержат одну
произвольную постоянную. Единственное
начальное условие для уравнения 1-го
порядка
уравнения 1-го порядка содержат одну
произвольную постоянную. Единственное
начальное условие для уравнения 1-го
порядка
 позволяет определить значение константы
из общего решения или из общего интеграла.
Таким образом, будет найдено частное
решение или, что тоже, будет решена
задача Коши.
позволяет определить значение константы
из общего решения или из общего интеграла.
Таким образом, будет найдено частное
решение или, что тоже, будет решена
задача Коши.
Геометрически
общее решение уравнения
1-го порядка представляет собой семейство
кривых на плоскости XOY,
не имеющих общих точек и отличающихся
друг от друга одним параметром –
значением константы C.
Эти кривые называются интегральными
кривыми для
данного уравнения. Интегральные кривые
уравнения
 обладают очевидным геометрическим
свойством: в каждой точке
обладают очевидным геометрическим
свойством: в каждой точке
 тангенс угла наклона касательной к
кривой равен значению правой части
уравнения в этой точке:
тангенс угла наклона касательной к
кривой равен значению правой части
уравнения в этой точке:
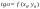 .
Другими словами, уравнение
.
Другими словами, уравнение
 задается в плоскости XOY
поле направлений касательных к
интегральным кривым.
задается в плоскости XOY
поле направлений касательных к
интегральным кривым.
Изоклиной ду называется множ-во точек пл-ти, в каждой из которых угловой коэф касательной к интегральным кривым этого ур-я имеет постоянное значение. Очевидно, ур-е изоклины имеет вид: f(x,y)=k, где к-значение углов коэфкачательной. Изоклины – линии уровня ф-цииf(x,y)
Пример.
Найти общее решение уравнения y'+3y=e2x
и частное решение,удовлетворяющее
начальным условиям х=0,
у=1.
Решение. Данное уравнение является
линейным..

Билет 19
![]()

![]()
Рассмотрим
![]()
![]()

![]()
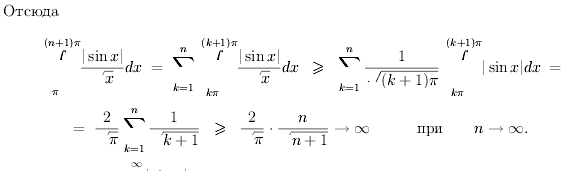
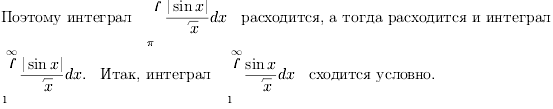
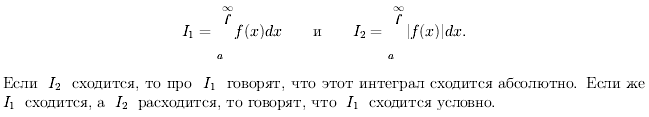

![]()





Билет 20
Несобственный
интеграл I=![]() называется: а)абсолютно
сходящимся,
если сходится интеграл
называется: а)абсолютно
сходящимся,
если сходится интеграл
![]() =
=![]() ,
в этом случае говорят, что ф-ция f абс.
интегрируема на промежутке [a;b); б)условно
сходящимся,
если интеграл I сходится, а
,
в этом случае говорят, что ф-ция f абс.
интегрируема на промежутке [a;b); б)условно
сходящимся,
если интеграл I сходится, а
![]() расходится.
расходится.
