
Лекции по физике 2 семестр / 31 ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
.docЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Основные положения. Уравнение Шредингера.
Создание квантовой теории связано с именами Бора, Шредингера, Гейзенберга, Паули, Борна и др. Теория атома, созданная Бором, называется старой квантовой теорией. Создание современной теории начинается с работы Гейзенберга. В ней Гейзенберг изложил матричный подход. Однако наибольшее распространение получил подход Шредингера (1926 г). Он основан на уравнение дифференциального уравнения в частных производных второго порядка. Современная квантовая теория основана на использование уравнения Шредингера. Это уравнение постулировалось в работах Шредингера. Он стремился избежать двойственности, которая возникает при изучении микромира. Но его работа положила началом новых исследований и осмысления полученных результатов. Окончательная интерпретация результатов применения уравнения Шредингера относится к 1933 г.
Нестационарное уравнение Шредингера имеет вид
 (1)
(1)
![]() - оператор Гамильтона или гамильтониан;
- оператор Гамильтона или гамильтониан;
![]() - волновая функция. Оператор Гамильтона
для одной частицы в потенциальном поле
- волновая функция. Оператор Гамильтона
для одной частицы в потенциальном поле
![]() имеет вид:
имеет вид:
 (2)
(2)
 - оператор Лапласа. Если параметры
системы не зависят от времени, получим
стационарное уравнение Шредингера
- оператор Лапласа. Если параметры
системы не зависят от времени, получим
стационарное уравнение Шредингера
![]() (3)
(3)
![]() - энергия частицы в стационарном
состоянии. Решение уравнение Шредингера
(3) с гамильтонианом (2) имеет много
значений. Соответствующим подбором
граничных условий из них выбирается
только некоторые из них. Они имеет
физический смысл. Оказывается, что
уравнения вида (3) – это уравнения на
собственные значения и функции. В целом
набор собственных значений,
- энергия частицы в стационарном
состоянии. Решение уравнение Шредингера
(3) с гамильтонианом (2) имеет много
значений. Соответствующим подбором
граничных условий из них выбирается
только некоторые из них. Они имеет
физический смысл. Оказывается, что
уравнения вида (3) – это уравнения на
собственные значения и функции. В целом
набор собственных значений,
![]() ,
образует энергетический спектр. Он
может быть дискретным, сплошным
(непрерывным) или смешанным, т.е. содержать
как дискретную, так и непрерывную части.
Шредингер решил это уравнение для атома
водорода и получил, в частности,
результаты Бора без привлечения
постулатов.
,
образует энергетический спектр. Он
может быть дискретным, сплошным
(непрерывным) или смешанным, т.е. содержать
как дискретную, так и непрерывную части.
Шредингер решил это уравнение для атома
водорода и получил, в частности,
результаты Бора без привлечения
постулатов.
Свойства волновой функции.
Очень много потребовалось, чтобы понять смысл волновой функции, которая является решением уравнения Шредингера. Если посмотреть на Ур. (3), нетрудно заметить, что энергию можно найти следующим образом
 (1)
(1)
Таким образом, замечаем, что в наблюдаемую
величину, энергию, волновая функция
входит квадратично. В общем случае
оказалось, что наблюдаемое значение
физической величины
![]() можно вычислить, используя решение Ур.
(3), по формуле
можно вычислить, используя решение Ур.
(3), по формуле
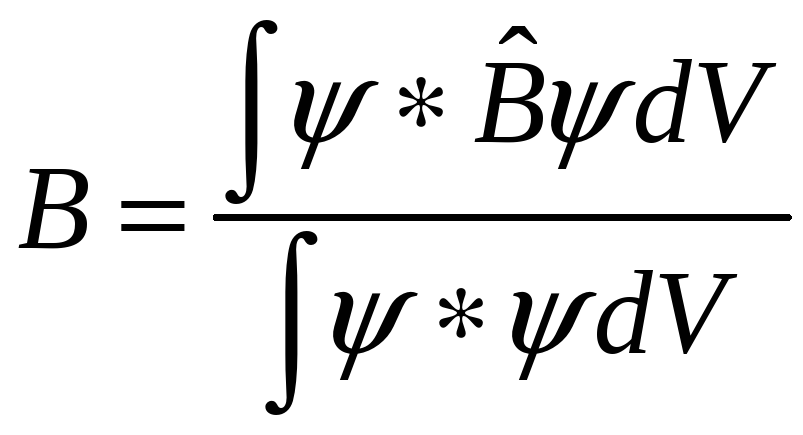 (2)
(2)
![]() - оператор рассматриваемой физической
величины. Отсюда можно заключить, что
сама волновая функция не имеет физического
смысла. Смысл имеет только квадратичная
форма. Введем величину
- оператор рассматриваемой физической
величины. Отсюда можно заключить, что
сама волновая функция не имеет физического
смысла. Смысл имеет только квадратичная
форма. Введем величину
![]() ,
которую можно рассматривать как плотность
вероятности. Если нормировать функцию
,
которую можно рассматривать как плотность
вероятности. Если нормировать функцию
![]() на единицу, тогда появляется вероятностная
трактовка волновой функции
на единицу, тогда появляется вероятностная
трактовка волновой функции
![]() (3)
(3)
Это вероятность обнаружить частицу в
объеме
![]() ,
окружающим точку
,
окружающим точку
![]() .
Таким образом, мы переходим от
детерминированного описания, которое
свойственно классической физике, к
вероятностному. Это особенность описания
микромира. В этом случае формуле (2) можно
интерпретировать как определение
среднего значения некоторой величины,
значения которой распределены с
плотностью вероятности
.
Таким образом, мы переходим от
детерминированного описания, которое
свойственно классической физике, к
вероятностному. Это особенность описания
микромира. В этом случае формуле (2) можно
интерпретировать как определение
среднего значения некоторой величины,
значения которой распределены с
плотностью вероятности
![]() .
.
Рассмотрим некоторые простейшие применения уравнения Шредингера. Волновые функции удовлетворяют принципу суперпозиции.
![]() .
(4)
.
(4)
где
![]() - собственные функции, соответствующие
стационарному состоянию с номером
- собственные функции, соответствующие
стационарному состоянию с номером
![]() .
.
Свободная частица.
Оператор Гамильтона для свободной частицы имеет вид
 .
Для одномерного случая
.
Для одномерного случая
 .
.
Уравнение Шредингера
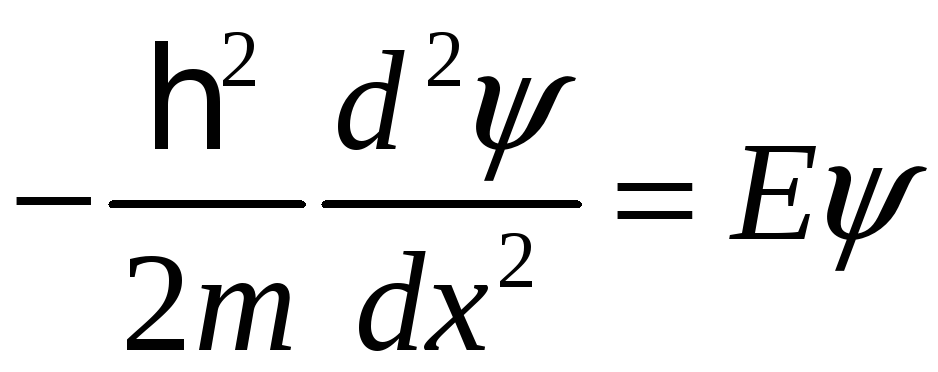 ,
,
Решение этого уравнения или собственные
функции:
![]() ,
,
![]() - нормировочный множитель.
- нормировочный множитель.
Значение энергии или собственные
значения:
 .
Энергетический спектр непрерывный.
.
Энергетический спектр непрерывный.
Потенциальная яма. Туннельный эффект.
Рассмотрим одномерную бесконечно
глубокую потенциальную яму. Потенциал
определяется как
![]() для
для
![]() ,
,
![]() для
для
![]() ,
,
![]() для
для
![]() .
.
Уравнение Шредингера
 ,
,
Решение с учетом граничных условий
 ,
,
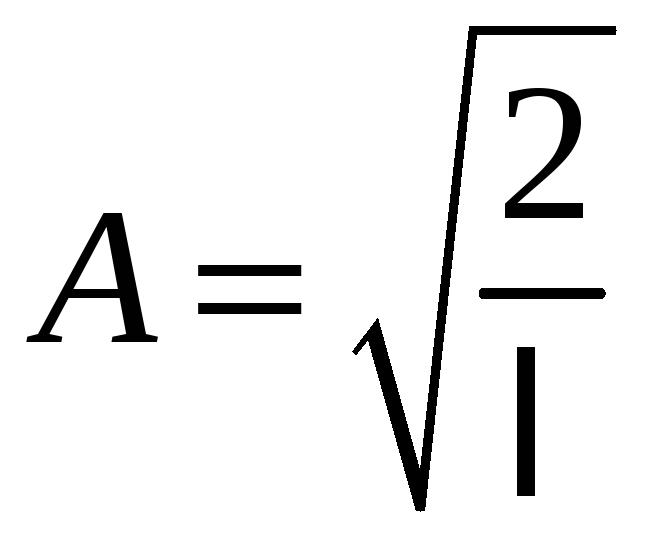 .
.
Энергия стационарного состояния равна
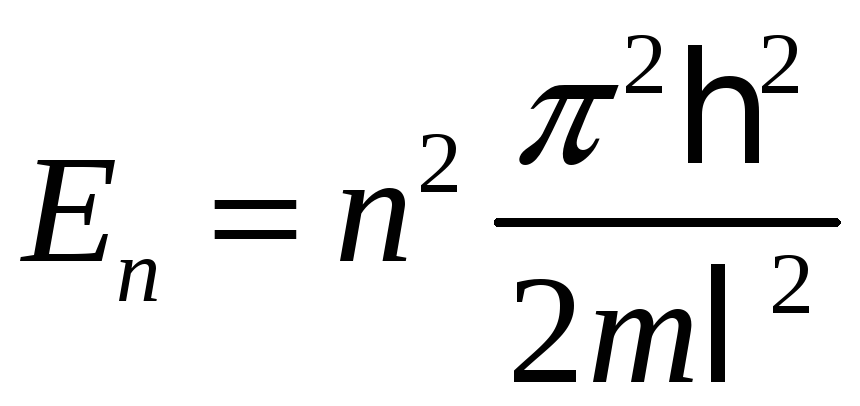 .
.
![]()
Видим, что энергетический спектр
дискретный. Т.о. энергия квантуется.
Энергия уровней растет квадратично с
ростом
![]() .
Число
.
Число
![]() определяет состояние частицы в
потенциальной яме. Его называют квантовым
числом. Это число не может равняться
нулю, ибо это соответствует отсутствию
частицы.
определяет состояние частицы в
потенциальной яме. Его называют квантовым
числом. Это число не может равняться
нулю, ибо это соответствует отсутствию
частицы.
Туннельный эффект.
Рассмотрим прохождение через потенциальный барьер конечной высоты. Потенциальная энергия в уравнении Шредингера имеет вид
1)
![]() для
для
![]() ,
,
2)
![]() для
для
![]() ,
,
3)
![]() для
для
![]() .
.
В общем виде уравнение Шредингера для всех областей запишется

Его решение
![]()
Где для области
![]() :
:
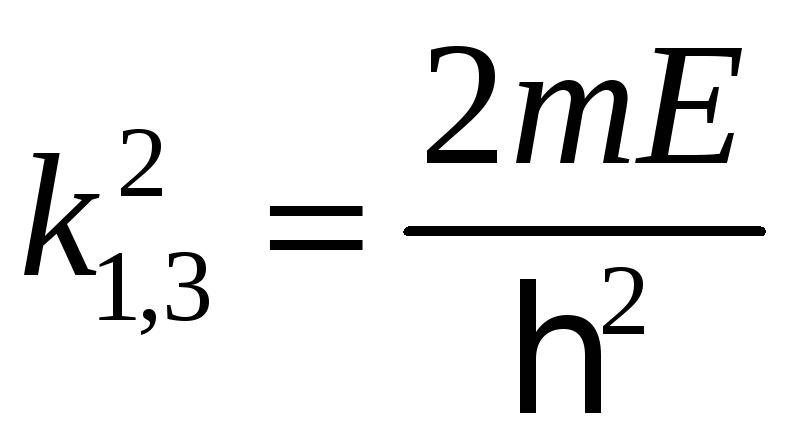 ,
,
для области
![]() :
:
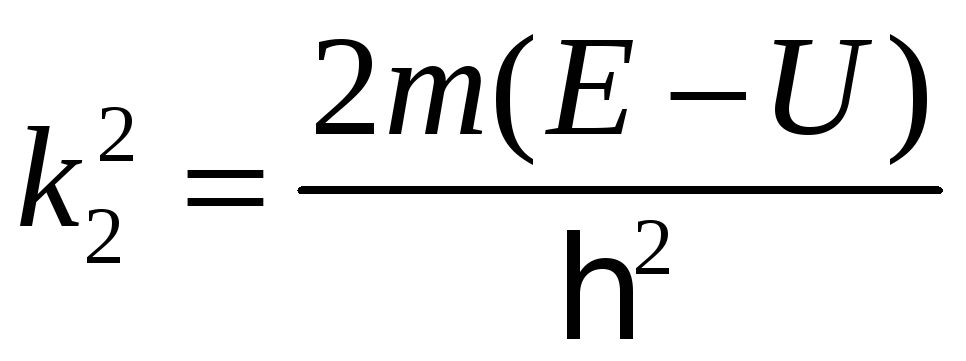 .
.
Рассмотрим случай
![]() .
Тогда
.
Тогда
![]() и
и
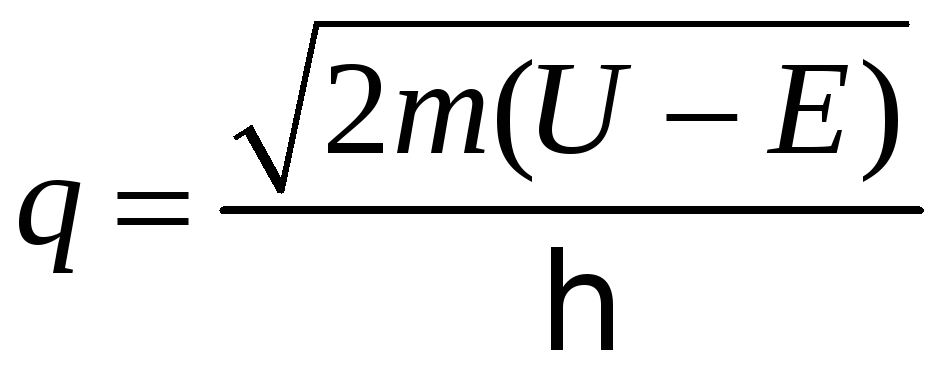 .
.
Волновая функция имеет вид
![]() ,
,
Поскольку волновая функция ограничена,
то
![]() .
Тогда
.
Тогда
![]()
Рассматривается движение частицы
слева направо через барьер. Поскольку
квадраты волновой функции определяют
плотности вероятности обнаружения
частицы в соответствующей области,
можно ввести коэффициент прозрачности
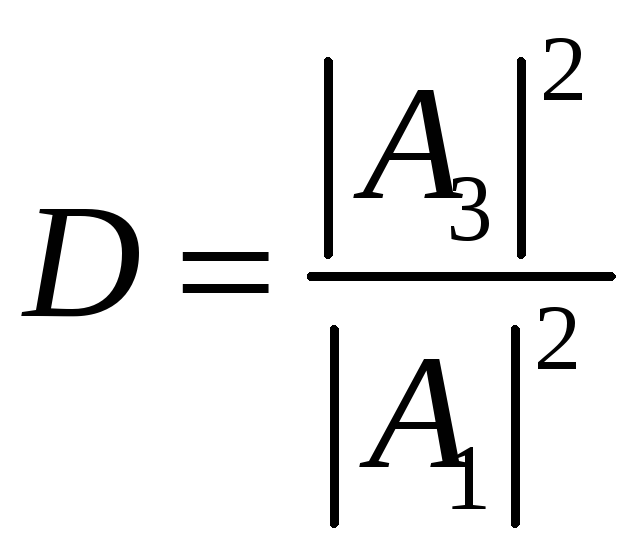 .
.
В силу непрерывности волновых функций сшиваем их на границах барьера и получим следующее выражение для коэффициента прозрачности
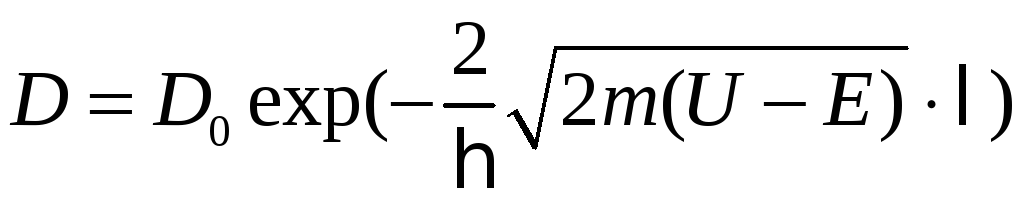 .
.
Постоянную
![]() можно положить равной единице. Для
потенциальной ямы произвольной формы
можно положить равной единице. Для
потенциальной ямы произвольной формы
 .
.
Таким образом, получили, что частица
может оказаться по другую сторону
потенциального барьера, высота которого
превышает энергию частицы. Вероятность
встретить частицу по другую сторону
барьера определяется коэффициентом
прозрачности. Это явление называется
туннельным эффектом. Подобная ситуация
никогда не может встретиться в классической
физике и в макромире. Туннельный эффект
активно используется при создании
устройств. На его основе был объяснен
![]() - распад ядер.
- распад ядер.
