
Lektsii_PDF / Лекция_13
.pdf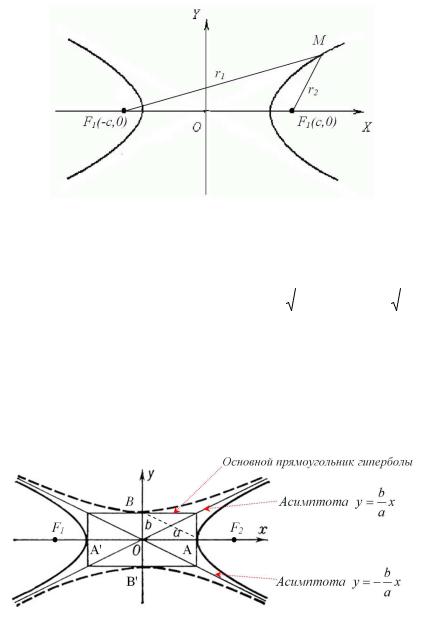
Лекция №13
Гипербола
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух точек плоскости, называемых фокусами F1 и F2 , есть величина постоянная, обозначаемая 2a .
Из |
F1MF2 следует, что r1 − r2 < 2c и тогда |
2a < 2c или a < c . Числа r1 и r2 |
|||||||||||
называются фокальными радиусами. Точка |
M (x, y) принадлежит гиперболе |
||||||||||||
|
|
r1 − r2 |
|
= 2a , |
|
|
− |
|
|
= 2a . |
|||
тогда и только тогда, когда |
|
|
то есть |
|
(x + c)2 + y2 |
(x − c)2 + y2 |
|
||||||
|
|
||||||||||||
|
уравнение гиперболы. |
|
|
его, |
|
|
|
||||||
Это |
|
Упростим |
применяя стандартный прием |
||||||||||
«уничтожения» радикалов. В результате получим каноническое уравнение
гиперболы: |
x2 |
− |
y2 |
= 1, где b2 = c2 − a2 . В каноническом уравнении может быть |
|
a2 |
b2 |
||||
|
|
|
как a > b, так и b > a .
Оси симметрии называются осями гиперболы, а центр симметрии (точка пересечения осей) – центром гиперболы. Одна из осей пересекается с гиперболой в двух точках, которые называются ее вершинами ( A1 и A2 ). Эта ось называется действительной осью гиперболы. Другая ось не имеет общих точек с гиперболой и называется мнимой осью: a - действительная полуось гиперболы, b - мнимая полуось.
1

|
При |
|
x |
|
→ ∞ |
ветви гиперболы в 1 и |
3 |
координатных |
четвертях |
|||||||||
|
|
|
||||||||||||||||
приближаются к прямой y = |
b |
x , а во второй и четвертой четверти – |
к прямой |
|||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
||
y = − |
b |
x . Пунктиром показана сопряженная |
гипербола. |
Ее каноническое |
||||||||||||||
|
||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнение |
x 2 |
− |
y 2 |
= −1 . Гипербола с равными полуосями |
a = b |
называется |
||||||||||||
a 2 |
b2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
равносторонней и ее каноническое уравнение x2 − y 2 = a2 |
|
|
|
|
||||||||||||||
|
Эксцентриситетом гиперболы называется |
отношение |
c |
, |
где c - |
|||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
||
половина расстояния меду фокусами, a - действительная полуось гиперболы.
Обозначается |
ε . Так как c > a , |
то |
ε > 1. |
Поскольку c2 = a2 + b2 , |
то |
|||||||||||
ε 2 = |
c2 |
= |
a2 + b2 |
= 1 + |
b2 |
. Следовательно, |
|
b |
= |
|
|
|
и если ε → 1, то |
b |
→ 0 , |
|
|
|
ε 2 − 1 |
то |
|||||||||||||
|
a2 |
|
a2 |
|
a2 |
|
|
a |
|
|
|
|
a |
|
||
есть основной прямоугольник более вытянут в направлении действительной оси.
Две прямые, перпендикулярные большой оси гиперболы и
расположенные симметрично относительно центра на расстоянии |
a |
от него, |
||||||
ε |
||||||||
называются директрисами гиперболы, где a - действительная полуось, ε |
- |
|||||||
эксцентриситет гиперболы. Их уравнения: x = − |
a |
, |
x = |
a |
. Так как |
ε > 1, |
то |
|
|
ε |
|
ε |
|
|
|||
εa < a . То есть правая директриса расположена между центром и правой вершиной гиперболы, а левая – центром и левой вершиной.
Теорема 1 |
|
|
|
|
Если r |
-расстояние от произвольной точки M гиперболы до какого-нибудь |
|||
фокуса, |
d - |
расстояние от той же точки до соответствующей этому фокусу |
||
директрисы, |
то |
r |
есть величина постоянная, равная эксцентриситету |
|
|
||||
|
|
|
d |
|
гиперболы.
2
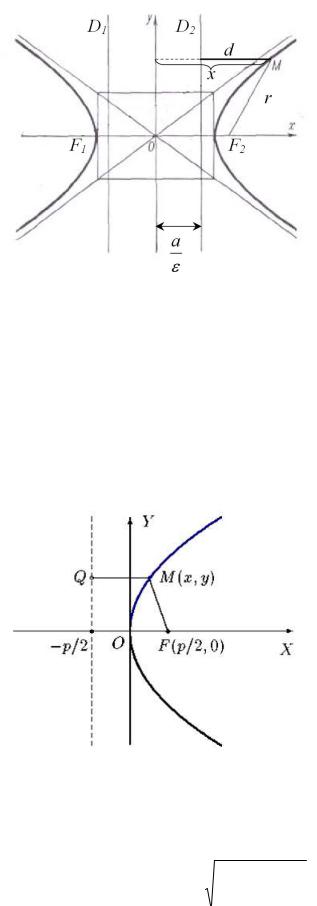
Парабола
Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F на плоскости, называемой фокусом, равно расстоянию до некоторой прямой, расположенной в этой плоскости, называемой директрисой параболы.
|
|
p 2 |
2 |
|
|
p |
|
|
|
|
|
|
|
|
|||||
Из определения следует, что |
r = d , то есть x − |
|
+ y |
|
= |
x + |
|
. |
Преобразуя |
|
|
2 |
|||||||
|
|
2 |
|
|
|
|
|
||
это выражение, получим каноническое уравнение параболы |
|
у2 |
= 2 px, p > 0 |
||||||
Параметр p называется |
фокальным параметром |
параболы, точка с |
|||||||
|
|
|
|
|
|
|
|
|
3 |

координатами |
p |
,0 |
- |
фокусом |
параболы, а |
уравнение x = - |
p |
является |
|||||||
|
|
||||||||||||||
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
уравнением директрисы. Точка O называется вершиной параболы. Ось |
|||||||||||||||
симметрии – ось OX - |
осью параболы. |
Число |
p выражает расстояние от |
||||||||||||
фокуса до директрисы. |
|
|
|
и M (1,− |
|
|
) (при x = 1 значение y = ± |
|
|
||||||
|
|
|
|
). |
|||||||||||
Рассмотрим точки M (1, 2 p) |
|
2 p |
2 p |
||||||||||||
Расстояние между ними 2
 2 p . Чем больше p , тем больше расстояние. То есть параметр p характеризует «ширину» области, ограниченную параболой.
2 p . Чем больше p , тем больше расстояние. То есть параметр p характеризует «ширину» области, ограниченную параболой.
Условно величину r назовем эксцентриситетом параболы.
d
Обобщенное определение этих линий второго порядка.
Геометрическое место точек плоскости, для которых отношение расстояния до некоторой точки F плоскости, называемой фокусом, к расстоянию до некоторой фиксированной прямой D , называемой директрисой, есть величина постоянная, называемая эксцентриситетом ε , будет эллипсом (0 £ ε < 1), параболой ε = 1, гиперболойε > 1.
Линии второго порядка, задаваемые общим уравнением.
Рассмотрим общее алгебраическое уравнение второй степени:
a x2 + 2a |
xy + a |
22 |
y2 + 2a |
x + 2a |
y + a = 0 , |
|
|
|
|
|
|
|
|
|
(1) |
|
|
|||||||
11 |
12 |
|
|
|
|
13 |
|
23 |
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
a x2 |
+ 2a xy + a |
22 |
y 2 |
- |
называется |
старшей |
|
группой, |
2a x + 2a |
23 |
y + a |
33 |
- |
||||||||||
|
11 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
||||
линейная часть уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Будем считать, что хотя бы один из коэффициентов a11 , a12 , |
a22 |
отличен |
|||||||||||||||||||||
от нуля. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Метод упрощения уравнения второй степени |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1. |
Если |
a11 - a22 ¹ 0 |
и |
a12 |
¹ 0 , |
то |
выполняем |
|
следующее |
действие: |
||||||||||||||
|
поворачиваем оси на угол α , |
для которого |
tg 2α = |
2a12 |
|
. При этом |
||||||||||||||||||
|
a11 − a22 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
формулы преобразования имеют вид: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x = x' cosα − y' sin α |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
y = x' sin α + y' cosα . |
|
|
|
|
|
|
|
|
|
|
||||
Подставив в (1) |
, получим: a ' |
x'2 |
+ a ' y'2 |
+ 2a' |
x + 2a |
' |
y + a' |
|
= 0 |
(2) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
11 |
|
22 |
13 |
23 |
33 |
|
|
|
|
|
|
|
|
||
(как видно, уничтожили слагаемое – произведение xy ). |
|
|
|
|
|
|
|
|||||||||||||||||
2. |
Если |
a12 |
= 0 , |
|
то |
фактически |
исходное уравнение имеет вид (2) и |
|||||||||||||||||
|
поэтому переходим ко второму этапу – пункту 5. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3. |
Если a12 ¹ 0 , а a11 = a22 , то ctg 2α = |
a11 − a22 |
= 0 , тогда 2α = ±90o и α = ±45o . |
||||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
2a12 |
|
|
|
|
|
|
|
|
|
|
|
|
4. |
Если a12 ¹ 0 , а a11 = 0 |
и |
a22 = 0 , |
то есть |
|
отсутствуют |
квадраты |
||||||||||
|
переменных, то в уравнении (1) делаем замену переменных x = x1 + y1 и |
||||||||||||||||
|
y = x1 - y1 , и получим уравнение, |
в |
котором |
|
присутствуют |
квадраты |
|||||||||||
|
новых переменных: x1 и |
y1 . Выполняем пункт 1 |
с соответствующими |
||||||||||||||
|
значениями переменных. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
' |
|
2 |
' |
|
|
' |
2 |
' |
|
|
||
|
|
|
|
a13 |
|
' |
|
|
a23 |
|
|
|
|||||
5. |
Выделим полные квадраты: |
a11(x |
+ |
|
) |
|
+ a22 |
y |
+ |
|
|
|
= k |
. |
(3) |
||
' |
|
' |
|||||||||||||||
|
|
|
|
|
|
a11 |
|
|
|
|
|
|
a22 |
|
|
|
|
6. Получив |
преобразованное уравнение |
и сделав замену переменных: |
|||||
x ' = x' + |
a13' |
и y ' = y' + |
a23' |
, получим: a (x ')2 |
+ a' |
(y ')2 = k '. |
|
a' |
a' |
||||||
|
|
11 |
22 |
|
|||
11 |
22 |
|
|
|
|||
Можно ли установить вид кривой, анализируя общее уравнение? Можно.
Инвариантом уравнения линии второго порядка (1) относительно преобразования декартовых координат называется функция f (a11 , a12 ,...a33 )
от коэффициентов aij этого уравнения, значение которой не изменяется при переходе к другой системе координат.
Теорема 13.2. Величины I1 = a11 + a22 , I2 |
= |
|
a11 |
a12 |
|
, I3 = |
a11 |
a12 |
a13 |
(2) |
|
|
|||||||||
|
|
a12 |
a22 |
a23 |
||||||
|
|
|
a12 |
a22 |
|
|
a13 |
a23 |
a33 |
|
|
|
|
|
|
|
|
|
являются инвариантами уравнения линии второго порядка (1) относительно преобразования декартовой системы координат.
Слово «инвариант» с латинского переводится как «неизменный». Если
(1) умножить или разделить на одно и то же число, то новое уравнение представляет ту же линию второго порядка, но I1, I2 , I3 - изменяются. Поэтому I1, I2 , I3 - инварианты уравнения, а не инварианты линии. Причем инварианты уравнения относительно преобразования декартовых координат.
В зависимости от инварианта I2 тип линий может быть :
∙эллиптический ( I2 > 0)
∙гиперболический(I2 < 0)
∙параболический(I2 = 0)
Рассмотрим: (Бахвалов С.В. и др. Аналитическая геометрия, 1970, стр.171.) 1. I 2 ¹ 0 . С помощью преобразования декартовой системы координат
(параллельный перенос и поворот осей) уравнение (1) приводится к
виду: a ' |
x'2 |
+ a ' |
y'2 |
+ |
I |
3 |
= 0 |
(3) |
|
|
|||||||
11 |
|
22 |
|
|
I |
|
|
|
|
|
|
|
|
2 |
|
|
Центральной линией называется линия, для каждой точки которой существует другая ее точка, расположенная симметрично относительно некоторой точки плоскости, называемой центом.
5
Уравнение (3) есть уравнение центральных линий, к ним относятся линии эллиптического и гиперболического типа.
a) |
I2 > 0 ; I2 = a11a22 - a122 |
> 0 . Следовательно, sign(a11 ) = sign(a22 ) = signI1 . |
||||||||||||||||
Не нарушая общности рассуждений, |
|
будем |
считать |
a11 > 0 , a22 > 0 . |
||||||||||||||
Очевидно, что I1 > 0 . Поскольку в противном случае, умножая исходное |
||||||||||||||||||
уравнение на -1 можно добиться, что I1 |
|
будет положительным, а при |
||||||||||||||||
этом I2 |
знака менять не будет. |
|
|
|
|
|
|
|
|
|
|
|||||||
Теорема 3. Пусть уравнение (1) эллиптического |
типа |
( I2 > 0) |
||||||||||||||||
преобразовано так, |
что I1 > 0 . Тогда при I3 < 0 мы получаем уравнение |
|||||||||||||||||
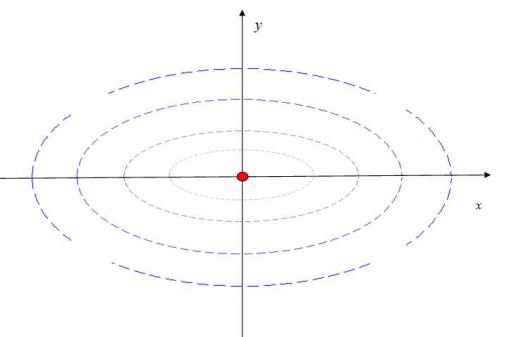
эллипса, при I3 = 0 |
- |
уравнение вырожденного в точку эллипса, при |
||||||||||||||||
I3 > 0 |
уравнение |
мнимого |
|
эллипса |
|
(нет |
ни одной |
точки, |
||||||||||
удовлетворяющей (13.1)). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Схема теоремы: |
|
I3 < 0 − эллипс |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
I2 |
> 0 и I1 > 0 , тогда |
I3 = 0 − точка |
|
. |
|
|
|
|||||||||||
|
|
|
> 0 − минимый эллипс |
|
|
|
|
|
||||||||||
|
|
I3 |
|
|
|
|
|
|||||||||||
b) |
I2 < 0 . Следовательно, |
|
a |
a |
|
= |
|
a' |
0 |
|
= a11' a22' < 0 . |
|
|
|||||
|
|
|
|
|
|
|||||||||||||
|
|
11 |
12 |
|
|
11 |
a' |
|
|
|
||||||||
|
|
|
|
|
|
a |
a |
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
12 |
22 |
|
|
|
|
22 |
|
|
|
|
|
Теорема 4. Пусть(1) – уравнение гиперболического типа ( I2 < 0 и для |
||||||||||||||||||
определенности считаем, что a11' |
|
> 0, а a22' |
|
< 0 ), тогда при I3 |
= 0 получаем |
|||||||||||||
уравнение пары пересекающихся прямых (вырожденную гиперболу),
при I3 ¹ 0 |
получаем |
|
уравнение гиперболы, причем, |
если |
|
I3 > 0 , |
то |
||||||||||||||||||||
действительная ось – |
|
есть ось OX . Если I3 < 0 , то действительная ось – |
|||||||||||||||||||||||||
ось OY . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Схема теоремы: |
|
|
< 0 − гипербола, действительнаяосьOY |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
I2 < 0, |
|
|
|
I |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
I3 = 0 − пересекающиеся прямые |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||
a11' > 0, a22' < 0 |
, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
> 0 − гипербола, действительнаяосьOX |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
I3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2. I2 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Покажем, что I1 ¹ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Доказательство: |
Предположим, |
что I1 = 0 . |
Тогда |
I1 = a11 + a22 |
= 0 . |
||||||||||||||||||||||
Возведем в квадрат: |
|
a2 + 2a a |
|
+ a2 |
= 0 .Тогда a a |
|
= - |
|
a2 |
- |
a2 |
. Но I |
|
= 0 |
|||||||||||||
|
22 |
22 |
|
|
11 |
22 |
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
11 |
11 |
|
22 |
11 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
- a 2 |
= 0 |
|
|
|
|
= a 2 . |
Следовательно: a2 |
= - |
|
a2 |
- |
|
a |
2 |
. Это |
|||||||||
то есть a |
a |
22 |
и |
a a |
22 |
|
11 |
|
|
|
22 |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
11 |
|
12 |
|
|
|
11 |
12 |
|
|
|
12 |
|
2 |
|
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
справедливо только в одном случае, если a11 = a22 |
= a12 = 0 . Но этого быть |
||||||||||||||||||||||||||
не может. Следовательно I1 ¹ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
В этом случае с помощью преобразования декартовой системы координат общее уравнение (1) приводится к следующему виду:
I |
y'2 + 2a ' |
x' + a' |
= 0 |
(4) |
1 |
13 |
33 |
|
|
Теорема 5. Пусть уравнение (1) есть уравнение параболического типа (I2 = 0) . Тогда при I3 ¹ 0 - это уравнение параболы, при I3 = 0 это уравнение распадается на уравнения двух параллельных прямых (в том числе и мнимых).
Схема теоремы: |
|
|
|
I3 ¹ 0 - парабола |
|
|
I3 = 0 − пара параллельных |
. |
I2 = 0 ( I1 ¹ 0 ), тогда |
||
|
|
|
или сливающихся или мнимых прямых |
|
|
Предельные случаи. 1) Эллипса: точка.
2) Гипербола: пара пересекающихся прямых.
7

3) Парабола: параллельные прямые.
Примеры. |
|
|
|
|
1. |
4x2 − 9 y2 = 0 распадается на |
два уравнения: 2x − 3 y = 0 , |
2x + 3y = 0 |
, |
|
описывающие пересекающиеся прямые в точке (0,0). |
|
|
|
2. |
x2 − 2xy + y 2 − 9 = 0 распадается |
на два уравнения: |
x − y + 3 = 0 |
, |
|
x − y − 3 = 0 - параллельные прямые. |
|
|
|
|
|
|
8 |
|
3. |
|
x2 − 2xy + y2 = 0 распадается на два уравнения: x − y = 0 , |
x − y = 0 - две |
||||||||||
|
сливающиеся прямые. |
|
|
|
|||||||||
4. |
|
x2 + |
1 |
y2 |
= 0 распадается на два уравнения: x + |
1 |
iy = 0 , x − |
1 |
iy = 0 - пара |
||||
|
|
|
|
||||||||||
|
|
|
4 |
|
2 |
|
2 |
|
|||||
|
мнимых прямых, пересекающихся в действительной точке (0,0). |
||||||||||||
5. |
|
x2 |
+ |
y2 |
|
= 1 - нет точек, удовлетворяющих этому уравнению, это |
|||||||
|
− 9 |
|
|
||||||||||
|
|
|
|
− 16 |
|
|
|
||||||
|
уравнение описывает мнимый эллипс. |
|
|
|
|||||||||
6. |
|
x2 − 2xy + y2 + 9 = 0 распадается на два уравнения: |
|
|
x − y + 3i = 0 , |
||||||||
|
|
x − y − 3i = 0 - пара мнимых параллельных прямых. |
|
|
|
||||||||
9
