Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технический университет им. А. Н. Туполева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lektsii_PDF / Лекция_10

.pdf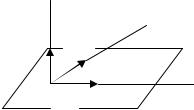

Скачиваний:

Добавлен:

22.03.2016

Размер:

69.18 Кб

Скачать

☆

Лекция № 10

Общее уравнение плоскости

Пусть дана произвольная декартовая система координат Oxyz .

Теорема 1. В декартовой системе координат любая плоскость описывается линейным уравнением:

Ax + By + Cz + D = 0	(10.1)
где A2 + B2 + C 2 ¹ 0	(10.2)

Обратно: Каждое уравнение (10.1) с условием (10.2) определяет некоторую плоскость.

Доказательство. Докажем первую часть.

Пусть дана произвольная плоскость π . Построим декартовую систему координат, разместив орты i, j на плоскости, а орт k π .

		Z
				Y
			j
			j

k
k
	i				X
	i				X

Тогда z = 0	-	линейное	уравнение
плоскости π : 0x + 0 y + 1z + 0 = 0 . При перемещении		системы	координат в
плоскости, сами координаты связаны соотношением:
x = α + x' cosϕ - y' sinϕ = F (x ', y')
1
y = β + x' sinϕ + y' cosϕ = F (x ', y')
2
Из этих соотношений видно, что координаты x, y	некоторой точки в первой

системе декартовых координат линейно выражаются через координаты x ', y' этой точки в другой системе координат, то есть F1, F2 - линейные. Аналогично можно получить и формулы преобразования в пространстве – сдвиг и поворот:

x = α + x' cos Ði'i + y' cos Ðj'i + z' cos Ðk 'i y = β + x' cos Ði' j + y' cos Ðj' j + z' cos Ðk ' j z = γ + x' cos Ði'k + y' cos Ðj'k + z' cos Ðk 'k

По условию теоремы в старой системе координат уравнение плоскости z = 0 . В новой системе координат это уравнение можно переписать:

x' cos Ði'k + y' cos Ðj'k + z' cos Ðk 'k + γ = 0 или Ax' + By' + Cz' + D = 0 , где

A2 + B2 + C 2 ¹ 0 , как направляющие косинусы вектора k , то есть одновременно все коэффициенты не могут равняться нулю.

Докажем вторую часть.

2. A = 0, By + Cz + D = 0 ,

параллельную оси

3. B = 0, Ax + Cz + D = 0 ,

параллельную оси

Рассмотрим некоторое линейное уравнение:

Ax + By + Cz + D = 0
где A2 + B2 + C 2 ¹ 0	(10.3)

Найдем геометрическое место точек, координаты которых удовлетворяют уравнению.

Рассмотрим точку M '(x , y , z			) :	Ax + By + Cz		0	+ D = 0 .	(10.4)
0	0	0		0	0	0

Такая точка всегда найдется, так как если C ¹ 0 , то задавая x0 , y0 , получим:

z = -	A	x -	B	y		-	D	. Вычтем из (10.3) выражение (10.4):

	C 0		C		0		C
A( x0 − x) + B ( y0 − y ) + C ( z0 − z ) = 0									(10.5)

Уравнение (10.5) эквивалентно (10.3), так как мы вычитали тождество. Докажем, что (10.5) определяет некоторую плоскость. Покажем, что

это будет плоскость, которая проходит через точку M '(x0 , y0 , z0 ) и ортогонально вектору n = {A, B,C}. Для этого рассмотрим произвольную точку

M (x, y, z) , принадлежащую плоскости. Тогда вектор

M 'M ^ n

имеет

= {(x - x), ( y

- y), (z

- z)},

координаты

M 'M

следовательно

- y) + C(z

- z) = 0 .

имеем:

Ax + By + Cz + D = 0 ,

(n, M 'M ) = A(x - x) + B( y

Отсюда

где D = -Ax0 - By0 - Cz0 .

Если точка M (x, y, z) не принадлежит плоскости, то

вектор M 'M не

и равенство (10.5) не выполняется.

ортогонален вектору n и (n, M 'M ) ¹ 0

Следовательно, уравнение (10.5) –

общее уравнение плоскости,

вектор

n = {A, B,C},

который

ортогонален

плоскости,

называется

нормальным

вектором плоскости. Следовательно, уравнение (10.3)

–

тоже

уранение

плоскости.

Неполное уравнение плоскости.

Если в общем уравнении (10.3)

A ¹ 0, B ¹ 0,C ¹ 0, D ¹ 0 ,

то уравнение

называется полным. В противном случае –

неполным уравнением.

Рассмотрим их:

1. D = 0, Ax + By + Cz = 0

Эта плоскость проходит через начало координат.

n = {0, B,C}. Это уравнение описывает плоскость

OX .

n = {A,0,C}. Это уравнение описывает плоскость

OY .

4. C = 0, Ax + By + D = 0 , n = {A, B,0}. Это уравнение описывает плоскость параллельную оси OZ .

5.	A = B = 0,Cz + D = 0 ,	n = {0,0,C}.	Это	уравнение	описывает	плоскость
	параллельную плоскости XOY .
6.	A = C = 0, By + D = 0 ,	n = {0, B,0}.	Это	уравнение	описывает	плоскость
	параллельную плоскости XOZ .
7.	B = C = 0, Ax + D = 0 ,	n = {A,0,0}.	Это	уравнение	описывает	плоскость
	параллельную плоскости YOZ .
8.	A = B = D = 0,Cz = 0 ,	n = {0,0,C}. Это уравнение описывает координатную
	плоскость XOY .	n = {0, B,0}. Это уравнение описывает координатную
9.	A = C = D = 0, By = 0 ,	n = {0, B,0}. Это уравнение описывает координатную

плоскость XOZ .

10. B = C = D = 0, Ax = 0 , n = {A,0,0}. Это уравнение описывает координатную плоскость YOZ .

Уравнение плоскости в отрезках

Пусть

дано

полное

уравнение

Ax + By + Cz + D = 0 , и

A ¹ 0, B ¹ 0,C ¹ 0, D ¹ 0 .

Тогда

= 1 ,

если обозначить a = −

,b = −

, c = −

, то получим

−

уравнение

плоскости в

отрезках

= 1 .

Числа a,b, c

- это

величины

отрезков,

отсекаемых

плоскостью

от

координатных

осей.

= 1

Например, решая систему :

= 0

получаем точку, в которой плоскость

= 0

пересекает ось OX : x = a, y = 0, z = 0 .

a b Y

Угол между двумя плоскостями.

Условия перпендикулярности и параллельности плоскостей. Пусть в декартовой системе координат заданы плоскости π1 и π 2 :

π1 : A1x + B1 y + C1z + D1 = 0 , n1 = {A1, B1,C1}

π2 : A2 x + B2 y + C2 z + D2 = 0 , n2 = {A2 , B2 ,C2 }

Угол ϕ между плоскостями равен углу между нормальными векторами n1 и

n2 : cosϕ =		A1 A2	+ B1B2 + C1C2					.

	A2	+ B2	+ C 2		A2	+ B2
							+ C 2
1		1	1	2		2	2

Условие параллельности плоскостей совпадает с условием коллинеарности

векторов n1 и n2 : A1 = B1 = C1 .

A2 B2 C2

Условие перпендикулярности плоскостей совпадает с условием перпендикулярности векторов n1 и n2 : A1 A2 + B1B2 + C1C2 = 0 .

Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой.

Пусть даны три точки: M1 (x1, y1, z1 ) , M 2 (x2 , y2 , z2 ) , M 3 (x3 , y3 , z3 ) .

Найдем два вектора M1M 2 = {x2 − x1, y2 − y1, z2 − z1}, M1M 3 = {x3 − x1, y3 − y1, z3 − z1}. Пусть M (x, y, z) - точка на плоскости, проходящей через три заданные точки.

Тогда M 1 M , M1M 2 , M1M3 - компланарные векторы, то есть справедливо равенство:

x − x

( )= − 1

M1M , M1M 2 , M1M3 x2 x1 x3 − x1

y − y1 y2 − y1 y3 − y1

z − z1

z2 − z1 = 0 . z3 − z1

Нормированное уравнение плоскости

Задана произвольная плоскость π .

	P	Y
	P	π
n		π
n
		M

Из начала координат проведем перпендикуляр к плоскости π . Он пересекает

π в точке P . На этой прямой изобразим

единичный

вектор n

того же

направления, что и вектор

. То есть n является ортом вектора

Дано: Пусть известны длина вектора

= p > 0 ,

n , и углы,

которые

образует вектор n с осями координат - α , β ,γ .Поэтому известны соответственные направляющие косинусы, которые являются координатами

вектора n : n = {cosα , cos β , cosγ }, n = cos2 α + cos2 β + cos2 γ = 1 .

Рассмотрим произвольную точку M плоскости π : (M π ) тогда и только тогда, когда выполняется следующее условие: прn OM = p .

Рассмотрим скалярное произведение(n,OM )= n прn OM = прn OM = p . С

другой стороны, поскольку известны координаты векторов, то справедливо следующее равенство: (n,OM )= x cosα + y cos β + z cosγ . Из двух последних

равенств следует: x cosα + y cos β + z cosγ = p или x cosα + y cos β + z cosγ - p = 0 ,

причем p > 0 .

Получим формулы преобразования от общего уравнения к

нормированному уравнению.
Пусть плоскость π	задана общим уравнением:	Ax + By + Cz + D = 0 и
нормированным уравнением: x cosα + y cos β + z cosγ - p = 0 ,		p ³ 0 .
Так как плоскость одна и та же, то существует число t , что справедливо:
tA = cosα , tB = cos β , , tC = cosγ , tD = - p .			(10.6)
Из свойства направляющих косинусов: cos2 α + cos2 β + cos2 γ = 1			следует, что
справедливо равенство:	t 2 ( A2 + B2 + C 2 ) = 1 . Отсюда имеем: t = ±		1	.

A2 + B2 + C 2

Так как p ³ 0 , то знак t противоположен знаку D , то есть signt = -signD . Для перехода от общего уравнения к нормированному необходимо:

1.вычислить t и взять его со знаком, противоположным D ;

2.вычислить cosα , cos β , cos γ , p по формулам (10.6);

3.записать уравнение x cosα + y cos β + z cosγ - p = 0 .

Соседние файлы в папке Lektsii_PDF

#
22.03.2016101.11 Кб35Лекция_1.pdf
#
22.03.201669.18 Кб33Лекция_10.pdf
#
22.03.201668.6 Кб32Лекция_11.pdf
#
22.03.201668.68 Кб32Лекция_12.pdf
#
22.03.2016264.18 Кб32Лекция_13.pdf
#
22.03.2016320.39 Кб31Лекция_14.pdf
#
22.03.2016563.08 Кб31Лекция_15.pdf