
Lektsii_PDF / Лекция_11
.pdf
Лекция № 11
Отклонение точки от плоскости
Пусть в декартовой прямоугольной системе координат задана некоторая
плоскость π своим уравнением: x cosα + y cos β + z cosγ − p = 0 , |
p > 0 |
(11.1) |
||
и задана точка |
M (x0 , y0 , z0 ) . Обозначим d - расстояние |
от точки |
M до |
|
плоскости π . |
|
|
|
|
Z |
Q |
|
|
|
|
|
|
|
|
|
|
M |
|
|
P |
π |
Y |
|
|
n |
|
|
||
|
|
|
||
X
Зная нормированное уравнение плоскости можно записать координаты орта нормали плоскости: n = {cosα , cos β , cosγ }; n = 
 cos2 α + cos2 β + cos2 γ = 1 , а также расстояние от начала координат до плоскости π : OP = p .
cos2 α + cos2 β + cos2 γ = 1 , а также расстояние от начала координат до плоскости π : OP = p .
Отклонением δ точки M от плоскости π называется число + d , если точка
M и начало координат лежат по разные стороны от плоскости π и число − d , если они лежат по одну сторону от плоскости.
Если начало координат принадлежит плоскости π , то δ = +d , если точка M расположена по ту сторону от π , куда направлен вектор n , и δ = −d - в противном случае.
Теорема 11.1. Отклонение точки M от плоскости π равно левой части уравнения (11.1) при подстановке в него координат точки:
δ = x0 cosα + y0 cos β + z0 cosγ − p
Доказательство. Спроецируем точку M на прямую, определенную вектором n . Обозначим проекцию через Q .
δ= PQ - длина направленного отрезка PQ .
δ= OQ − OP ;
где, OQ = прn OM = n прn OM = (n,OM ) = x0 cosα + y0 cos β + z0 cosγ , а OP = p
Таким образом: δ = x0 cosα + y0 cos β + z0 cosγ − p .
Пучки и связки плоскостей
Совокупность всех плоскостей, проходящих через некоторую прямую L в пространстве, называется пучком плоскостей с центром на L .
1
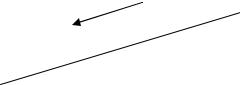
Теорема 11.2.
Если A1x + B1 y + C1z + D1 = 0 и A2 x + B2 y + C2 z + D2 = 0 - есть уравнения двух различных и не параллельных плоскостей, пересекающихся по некоторой прямой L , а α ¹ 0 и β ¹ 0 - произвольные числа, то уравнение
α (A1x + B1 y + C1z + D1 )+ β (A2 x + B2 y + C2 z + D2 ) = 0 |
(11.2) |
будет определять плоскость, проходящую через прямую L . |
|
Обратно. Каждая плоскость, проходящая через прямую L , будет описываться |
|
уравнением (11.2), где α и β - произвольные числа, |
не равные нулю |
одновременно. |
|
Совокупность всех плоскостей, проходящих через данную точку M (x0 , y0 , z0 ) ,
называется связкой плоскостей с центром в точке M .
Уравнение связки плоскостей имеет следующий вид:
A(x - x0 ) + B(y - y0 ) + C(z - z0 ) = 0 , |
(11.3) |
где A2 + B2 + C 2 ¹ 0
Уравнение прямой в пространстве
1. Каноническое уравнение прямой
Любой ненулевой вектор, параллельный данной прямой, называется
направляющим вектором прямой.
Получим уравнение прямой , проходящей через заданную точку M1 (x1, y1, z1 ) и имеющий заданный направляющий вектор q = {l, m, n}.
q
.
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 (x1, y1, z1 ) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M (x, y, z) |
|
|
|
|
|
|
|
= {x − x1, y − y1, z − z1}. |
|
|
|
||
|
|
|
|
|
|
|
|
|
M1M |
|
|
|
|
Точка M принадлежит искомой прямой тогда и только тогда, когда |
|
|
|||||||||||
M1M |
|||||||||||||
и q коллинеарные. |
В этом случае выполняется условие коллинеарности |
||||||||||||
векторов – пропорциональность координат этих векторов: |
|
|
|
||||||||||
|
x − x1 |
= |
y − y1 |
= |
z − z1 |
|
(11.4) |
||||||
|
l |
m |
n |
||||||||||
|
|
|
|
|
|
||||||||
В уравнении (11.4) одно или два числа из l, m, n могут быть равны 0. Если равен нулю некоторый знаменатель, то будем понимать, что равен нулю и числитель:
Примеры.
2

1. |
|
x - 5 |
= |
y - 0 |
= |
z -1 |
. |
Выражение |
x - 5 |
|
|
условно |
|
означает, что x − 5 = 0 . |
|||||||||
0 |
|
|
|
|
|||||||||||||||||||
|
|
|
6 |
4 |
|
0 |
|
|
|
|
|
|
|
|
|
z -1 |
|
||||||
|
Другими словами эта запись означает: x − 5 , |
y |
= |
. |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
4 |
|
|||||||
2. |
Каноническое уравнение прямой, |
проходящей через точки A(2,4,3) и |
|||||||||||||||||||||
|
|
B(2,4,5) |
имеет следующий вид: |
x - 2 |
= |
y - 4 |
= |
z - 3 |
. Эта запись означает: |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
2 |
|
|
|
|||||
x = 2 , y = 4 , z принимает любые значения для различных точек AB . Это уравнение описывает прямую, параллельную оси OZ , направляющий вектор имеет координаты
Пусть прямая задана пересечением двух плоскостей:
A1x + B1 y + C1z + D1 = 0A2 x + B2 y + C2 z + D2 = 0
прямой так как
(11.5)
Поскольку плоскости различные и не параллельные, то будет нарушаться
какое-нибудь из |
соотношений: |
A1 |
|
= |
B1 |
|
= |
C1 |
. Допустим: |
|
A1 |
¹ |
B1 |
. |
Тогда |
|
|
|
|
|
|
||||||||||
|
|
A2 |
|
B2 |
|
C2 |
|
|
A2 |
|
B2 |
|
|||
D = A1B2 - A2 B1 ¹ 0 . |
Определим точку |
|
на |
прямой (11.5). |
Для |
этого, |
взяв |
||||||||
произвольным z1 , найдем x1, y1 , как решение системы (11.5). найденная точка M1 принадлежит обоим плоскостям.
Очевидно, что если нормали плоскостей n1 и n2 ортогональны плоскостям, то они ортогональны и направляющему вектору прямой.
Следовательно: q ^ n1 |
|
и q ^ n2 . Тогда с одной стороны q = li + mj + nk , с другой |
|||||||||||||||||||||||||||||
стороны q = [n1, n2 ] = |
|
i |
|
j |
k |
|
и можно записать: |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
A1 |
|
B1 |
C1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
B2 |
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q = [n , n ] = li + mj + nk = |
|
i |
j |
|
k |
|
. |
Отсюда следует, что l = |
|
B1 |
C1 |
|
, m = |
|
C1 |
A1 |
|
, |
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
A |
B |
C |
|
|
|
|
|
|||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
B2 |
C2 |
|
|
|
C2 |
A2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
B2 |
C2 |
|
|
|
|
|
|
|
|
|
|||||
n = |
|
A1 |
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
виде будет: |
||||||||||||
|
|
|
|
и тогда |
|
уравнение |
прямой в каноническом |
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
A2 |
|
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x - x1 |
= |
y - y1 |
= |
z - z1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
l |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2. |
|
Уравнение прямой, проходящей через две различные точки |
|
|
|
||||||||||||||||||||||||||
Пусть заданы две различные точки M1 (x1, y1, z1 ) и M 2 (x2 , y2 , z2 ) . Определяем вектор M1M 2 = {x2 - x1, y2 - y1, z2 - z1} - он будет направляющим.
3

.
. M1 (x1, y1, z1 )
M 2 (x2 , y2 , z2 )
В этом случае уравнение прямой запишется следующим образом:
|
|
|
|
|
|
|
x − x1 |
|
= |
|
y − y1 |
= |
z − z1 |
|
(11.6) |
|
|
|
|
|
|
|
|
x2 − x1 |
|
y2 − y1 |
z2 − z1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
3. |
Параметрическое уравнение прямой. |
|
||||||||||||||
Соотношение (11.4) запишем следующим образом: |
|
|||||||||||||||
|
x − x1 |
= t |
; |
y − y1 |
= t ; |
z − z1 |
= t . |
|
|
|
(11.7) |
|||||
|
|
m |
|
|
|
|
||||||||||
|
l |
|
|
|
|
|
n |
|
|
|
|
|
|
|
||
Так |
как |
числа |
l, m, n |
одновременно не равно нулю, а |
числитель может |
|||||||||||
принимать любые значения, то очевидно, что областью изменения параметра t является интервал от − ∞ до ∞ . Из соотношений (11.7) следует:
x = x1 + lt ; y = y1 + mt ; z = z1 + nt |
(11.8) |
||||||||||||
|
|
|
|
|
|
|
|
|
Угол между прямыми в пространстве |
|
|||
Пусть L1 и L2 заданы каноническими уравнениями: |
|
||||||||||||
L : |
x − x1 |
= |
|
y − y1 |
= |
z − z1 |
|
|
|
||||
|
|
|
|
|
|
||||||||
1 |
|
l1 |
|
|
|
m1 |
|
|
n1 |
|
|||
|
|
|
|
|
|
|
|
||||||
L : |
x − x2 |
|
= |
y − y2 |
= |
z − z2 |
|
(11.9) |
|||||
|
|
|
|
||||||||||
2 |
|
l2 |
|
|
|
m2 |
|
|
n2 |
|
|||
|
|
|
|
|
|
|
|
||||||
Тогда угол между этими прямыми определяется углом между их
направляющими векторами: |
q1 = {l1, m1, n1}, q2 = {l2 , m2 , n2 }, который вычисляется |
||||||||||||||
как обратная тригонометрическая функция к значению: |
|||||||||||||||
cosϕ = |
( |
q1, q2 ) |
= |
|
|
l1l1 + m1m2 + n1n2 |
|
|
(11.10) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
q1 |
q2 |
|
|
|
l 2 |
+ m2 |
+ n2 |
|
l 2 + m2 |
+ n2 |
|||
|
|
|
|
|
|
|
1 |
1 |
1 |
2 |
2 |
2 |
|
|
|
Прямые параллельны, если векторы q1 и q2 коллинеарные, и следовательно выполняется условие пропорциональности их координат:
l1 |
= |
m1 |
= |
n1 |
(11.11) |
|
l2 |
m2 |
n2 |
||||
|
|
|
Прямые перпендикулярны друг другу, если векторы q1 и q2 ортогональные, и следовательно выполняется условие равенства нулю их скалярного произведения:
l1l1 + m1m2 + n1n2 = 0 |
(11.12) |
4
Условие принадлежности двух прямых одной плоскости
Пусть заданы две произвольные прямые L1 и L2 своими каноническими уравнениями (11.9). Указанные уравнения могут: пересекаться, быть параллельными, скрещиваться. Очевидно, что в первых двух случаях они
лежат в одной плоскости. |
|
|
|
|
|
||||||||
|
|
Прямые находятся в одной плоскости тогда и только тогда, когда |
|||||||||||
векторы |
|
= {x2 − x1, y2 − y1, z2 − z1}, |
q1, q2 - компланарные, то есть их |
||||||||||
M1M 2 |
|||||||||||||
смешанное произведение равно 0: |
|
|
|
||||||||||
|
x2 − x1 |
y2 − y1 |
z2 − z1 |
|
= 0 |
|
|
|
(11.13) |
||||
|
|
|
|
||||||||||
|
l1 |
m1 |
|
n1 |
|
|
|
|
|||||
|
l1 |
m2 |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
Прямые пересекаются, когда выполняется (11.13) и не выполняется |
|||||||||||
хотя бы одно из соотношений: |
l1 |
= |
m1 |
= |
n1 |
. |
|||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
l2 |
|
m2 |
|
n2 |
|
Прямые скрещиваются, если не выполняется условие (11.13).
Угол между прямой и плоскостью.
Пусть заданы прямая и плоскость:
π : Ax + By + Cz + D = 0 |
|
|||||||
L : |
x − x1 |
= |
y − y1 |
= |
z − z1 |
. |
|
|
|
|
|
|
|||||
|
l |
|
|
m |
n |
|
||
|
|
Из уравнений видно, |
что нормалью плоскости является вектор n с |
|||||
координатами: |
n = {A, B,C}, |
а направляющим вектором прямой - вектор |
||||||
q = {l, m, n}. |
|
|
|
|||||
|
|
|
|
|
|
|
ψ |
q |
|
|
|
|
|
|
n |
||
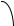 ϕ
ϕ
Тогда угол между прямой и плоскостью определяется через угол между их направляющим вектором q = {l, m, n} и нормалью n = {A, B,C} следующим образом:
cos(π − ϕ) = |
( |
n, q) |
= |
|
|
|
|
Al + Bm + Cn |
|
или |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
n |
q |
|
|
|
|
A2 + B2 + C 2 l 2 + m2 + n2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
sinϕ = |
|
|
|
|
Al + Bm + Cn |
|
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
A2 |
+ B2 + C 2 |
|
l 2 + m2 + n2 |
|
|
|||||||||||
Условие параллельности прямой и плоскости совпадает с условием ортогональности векторов n и q :
5

Al + Bm + Cn = 0 .
Условие перпендикулярности прямой и плоскости совпадает с условием коллинеарности векторов n и q :
A = B = C .
l |
m n |
Условие принадлежности прямой L к плоскости π определяется |
|
следующим соотношением: |
|
Ax1 + By1 + Cz1 + D = 0 |
|
|
Al + Bm + Cn = 0 |
|
|
6
