Lektsii_PDF / Лекция_15

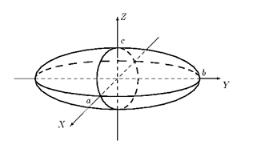
Лекция №15 Исследование формы поверхностей второго порядка по их каноническим

уравнениям.

1. Эллипсоид

Поскольку x,y,z во второй степени, то координатные плоскости являются плоскостями симметрии, а начало координат – центром симметрии.

Выясним форму эллипсоида, пересекая его плоскостями, параллельными координатной плоскости Oxy. Эти плоскости будут иметь уравнение Z=h, где h- константа.

Линию пересечения плоскости Z=h с эллипсоидом обозначим Lh. . Подставим Z=h в (1), получим:

В уравнении (1) a,b,c – отрезки, которые отсекает эллипсоид по соответствующим координатным осям.

Пересекая поверхность плоскостями X=h и Y=h получим подобные уравнения эллипсов.

2. Гиперболоид.

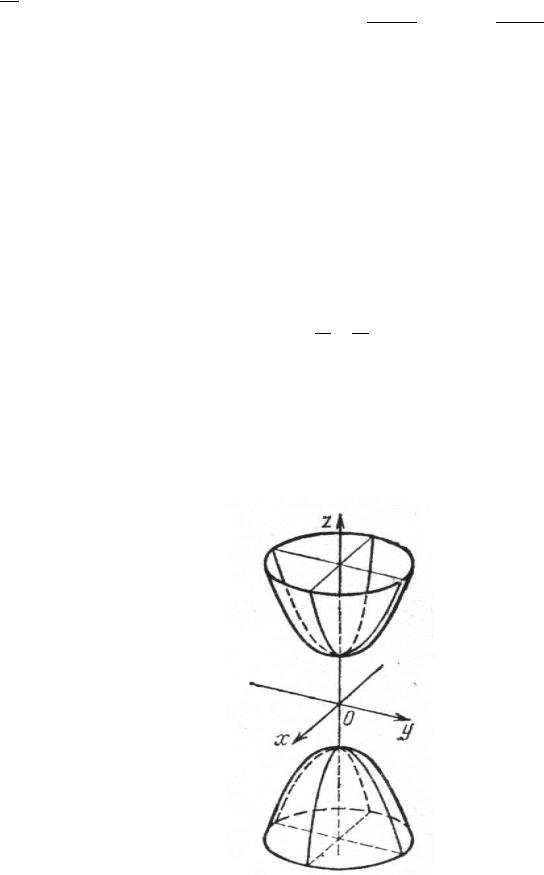
2.1.Двуполостный гиперболоид.

А) Выясним форму гиперболоида, пересекая его плоскостями, параллельными координатной плоскости Oxy. Эти плоскости будут иметь уравнение Z=h, где h- константа.

Выясним форму гиперболоида, пересекая его плоскостями, параллельными координатной плоскости Oxy. Эти плоскости будут иметь уравнение Z=h, где h- константа. Линию пересечения плоскости Z=h с гиперболоидом обозначим Lh.. Подставим Z=h в (2), получим:

Уравнение описывает поверхность S в пространстве, если :

1.координаты x,y,z точки, принадлежащей поверхности S, удовлетворяют уравнению

(4).

2.координаты x,y,z точки, не принадлежащей поверхности S, не удовлетворяют уравнению (4).

Замечание: не уравнение вида (4) является уравнением некоторой поверхности, например:

2 + 2 + 2 + 1 = 0 – не описывает поверхность

2 + 2 + 2 = 0 − описывает точку

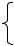
Пример: Сфера – это геометрическое место точек, расстояние от которых до некоторой фиксированной точки равно R.

Каждое из уравнений (5) описывает некоторую поверхность. Пусть эти поверхности пересекаются. Тогда линией пересечения этих поверхности будет некоторая кривая L. Поэтому естественно считать, что уравнения (5) задают некоторую кривую L в пространстве, если:

1)координаты x,y,z любой точки, принадлежащей L, одновременно удовлетворяют обоим уравнениям;

2)координаты x,y,z любой точки, не принадлежащей L, одновременно не удовлетворяют обоим уравнениям.

Уравнение цилиндрической и конической поверхностей.

Поверхность S называется цилиндрической с образующей, параллельной оси OZ, если для нее выполняется следующее свойство: прямая, проведенная через любую точку M( 0, 0, 0), которая принадлежит S, параллельно оси OZ целиком принадлежит этой поверхности S.

Аналогично можно дать определение цилиндрической поверхности с образующей,

Доказательство.

Рассмотрим 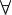точку M( 0, 0, 0), принадлежащую S. Тогда F( 0, 0)=0.

Проведем через точку 0 прямую, параллельную оси OZ. Возьмем на этой прямой точку M(x,y,z). Очевидно, что для всех точек этой прямой справедливо: x= 0, y= 0, а следовательно F( 0, 0)=0. Отсюда следует, что все точки прямой принадлежат S, то есть S – цилиндрическая поверхность. Доказательство завершено.

описывает кривую в плоскости Oxy

Поверхность S называется конической поверхностью с вершиной в начале координат, если прямая, проходящая через произвольную точку этой поверхности (отличную от начала координат) и начало координат целиком принадлежит поверхности S.

Функция F(x,y,z) называется однородной степени n, если для действительного числа k справедливо:

Рассмотрим произвольную точку M( 0, 0, 0), принадлежащую S:

F( 0, 0, 0) = 0

Проведем прямую через начало координат и точку 0.

Поверхности вращения.

Поверхность S называется поверхностью вращения с осью d, если она состоит из окружностей с центром на оси d, расположенными в плоскостях, ортогональных оси d. То есть поверхность вращения образуется при вращении некоторой линии L вокруг оси d (например, оси OZ).

Пример. Эллипсоид вращения.

2 + 2 + 2 = 1 - уравнение эллипсоида вращения

2 2 2

Однополостный гиперболоид вращения:

Эллиптический параболоид вращения:

2 22 + 2 =