3.2. Моменты инерции сечений

Моментами инерции сечений называются интегралы следующего вида:

– осевой момент инерции сечения относительно оси у;

– осевой момент инерции сечения относительно оси z;

– центробежный момент инерции сечения;

– полярный момент инерции сечения.

3.2.1. Свойства моментов инерции сечения

Размерность моментов инерции – [длина⁴], обычно [м⁴] или [см⁴].

Осевые и полярный моменты инерции всегда положительные. Центробежный момент инерции может быть положительным, отрицательным или равным нулю.

Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции сечения.

Оси симметрии всегда главные. Если из двух взаимно перпендикулярных осей хотя бы одна является осью симметрии, то обе оси главные.

Момент инерции составного сечения равен сумме моментов инерции элементов этого сечения.

Полярный момент инерции равен сумме осевых моментов инерции.

Докажем последнее свойство. В сечении с площадью А для элементарной площадки dA радиус-вектор ρ и координаты у и z (рис. 6) связаны по теореме Пифагора: ρ² = у² + z². Тогда

.

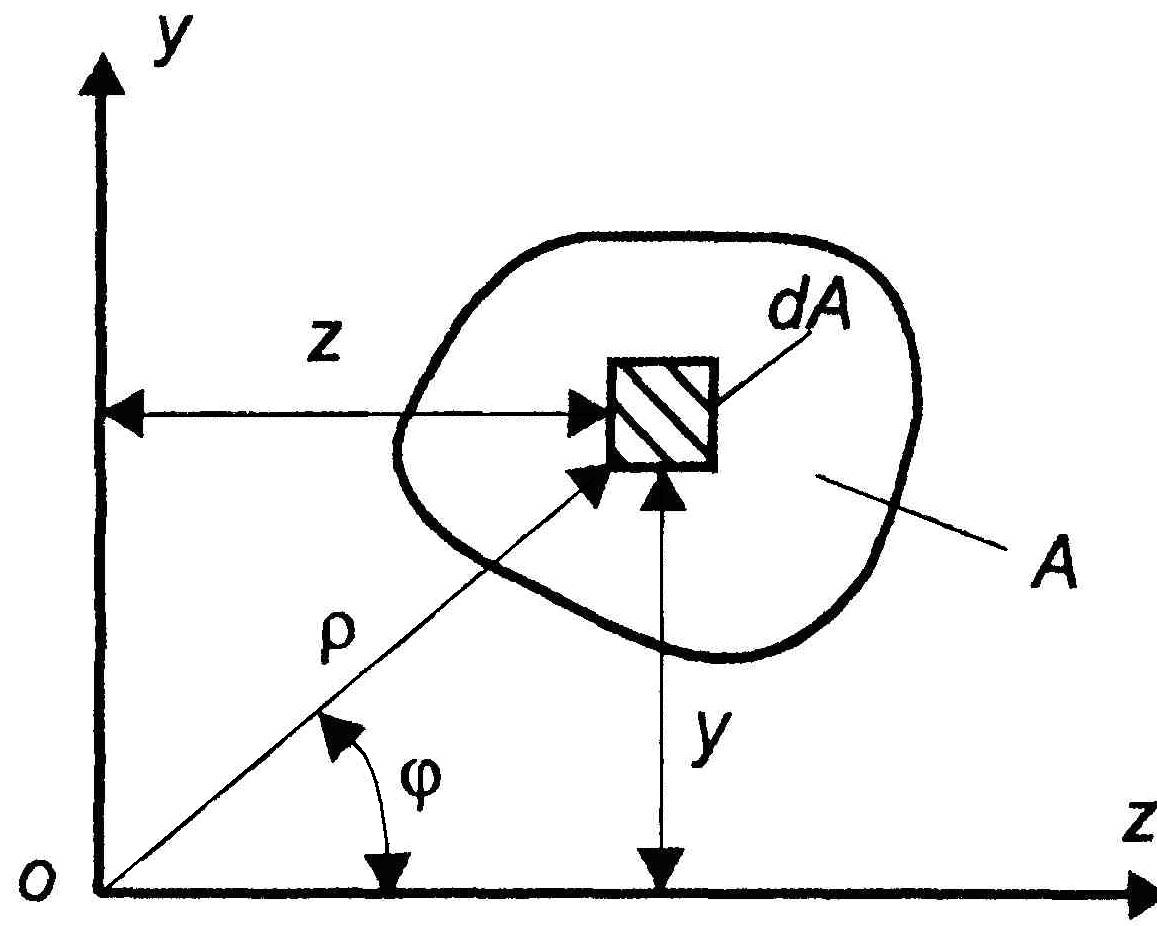
Рис. 6. Связь полярных и декартовых координат

элементарной площадки

3.2.2. Моменты инерции простейших фигур

В прямоугольном сечении (рис. 7) выберем элементарную площадку dA с координатами y и z и площадью dA = dydz.

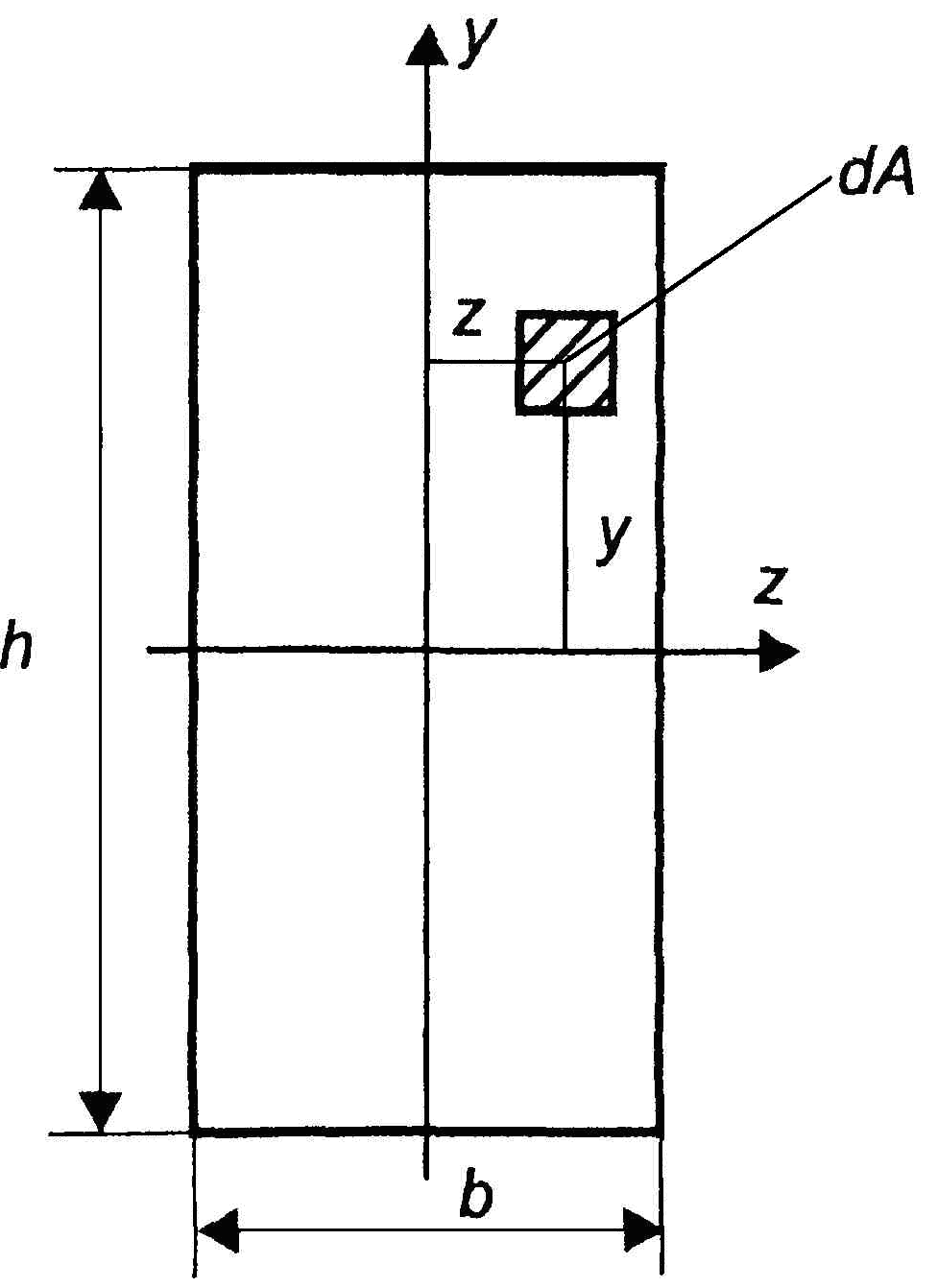
Рис. 7. Прямоугольное сечение

Осевой момент инерции относительно оси у

.

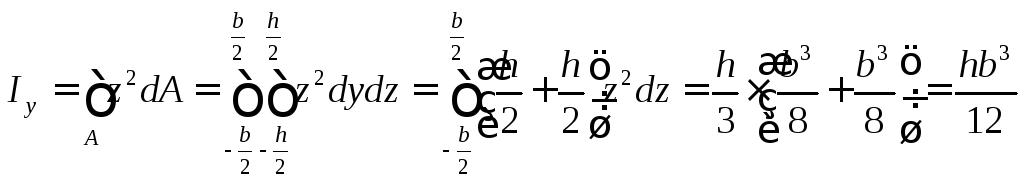Аналогично получаем момент инерции относительно оси z:

.

Поскольку у и z – оси симметрии, то центробежный момент D_zy = 0.

Для круга диаметром d вычисления упрощаются, если учесть круговую симметрию и использовать полярные координаты. Возьмем в качестве элементарной площадки бесконечно тонкое кольцо с радиусом ρ и толщиной dρ (рис. 8). Его площадь dA = 2πρdρ. Тогда полярный момент инерции:

.

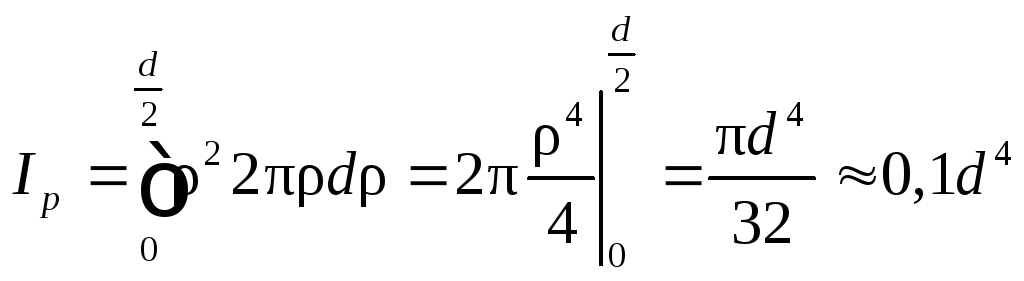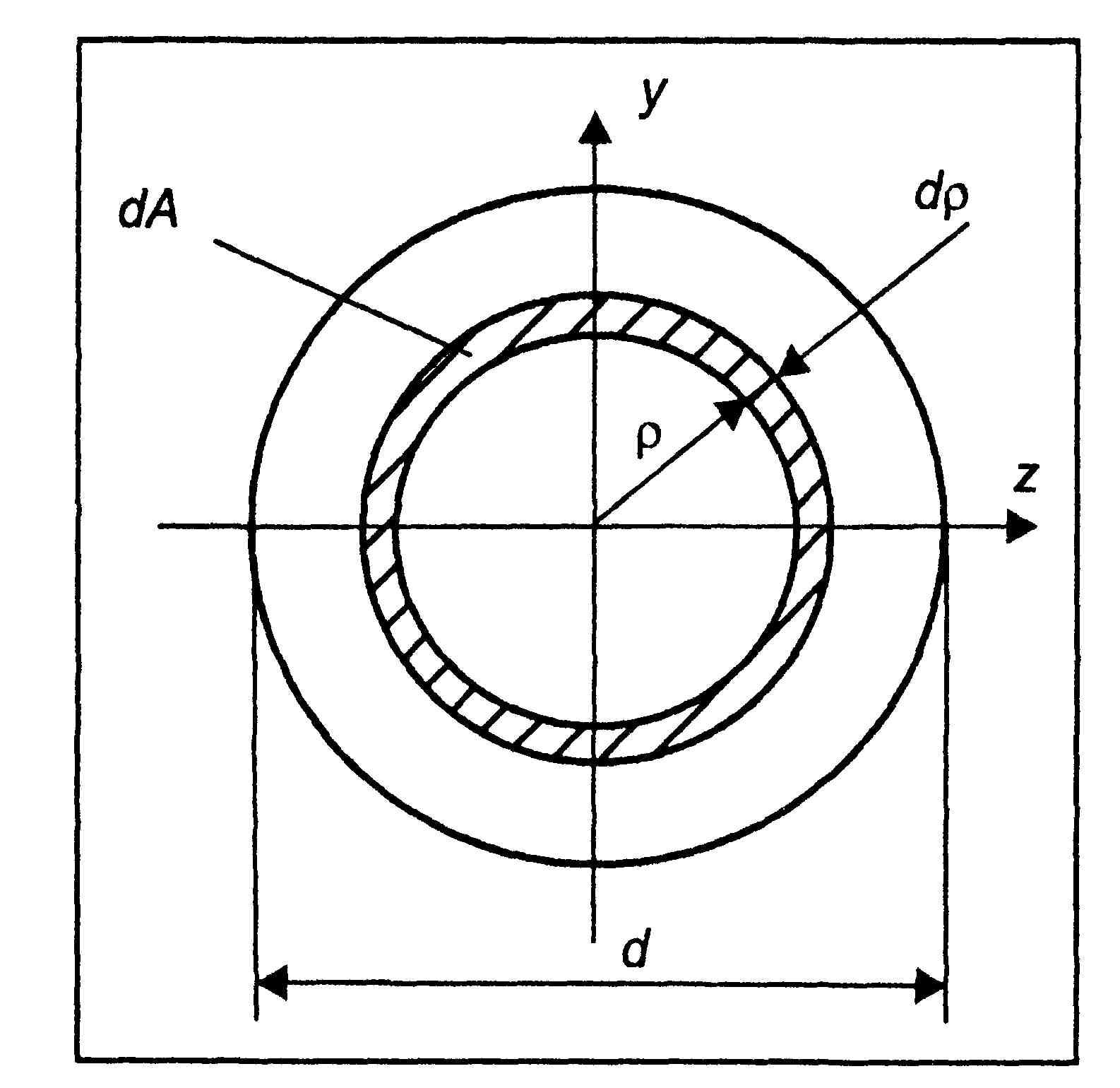
Рис. 8. Круглое сечение

Как показано выше, осевые моменты инерции относительно любой центральной оси одинаковы и равны

.

Момент инерции кольца находим как разность моментов инерции двух кругов – наружного (с диаметром D) и внутреннего (с диаметром d):

,

,

где .

Момент инерции I_zтреугольникаопределим относительно оси, проходящей через центр тяжести (рис. 9). Очевидно, ширина элементарной полоски, находящейся на расстоянииуот осиz, равна

Следовательно,

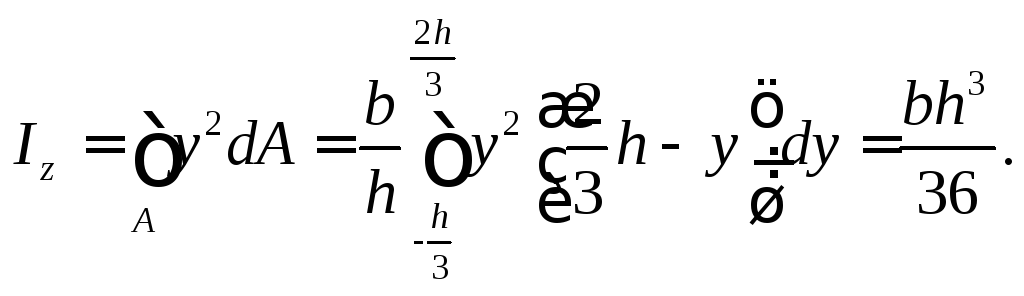
Рис. 9. Треугольное сечение

3.3. Зависимости между моментами инерции относительно параллельных осей

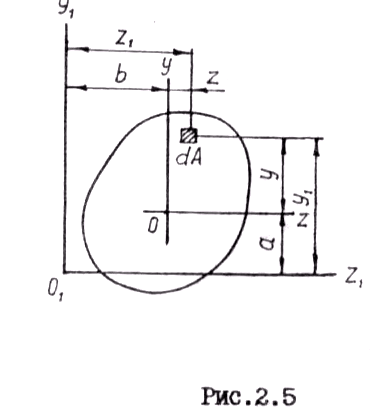
При известных величинах моментов инерции относительно осей z и у определим моменты инерции относительно других осей z₁ и y₁, параллельных заданным. Пользуясь общей формулой для осевых моментов инерции, находим

Если оси z и y центральные, то , и

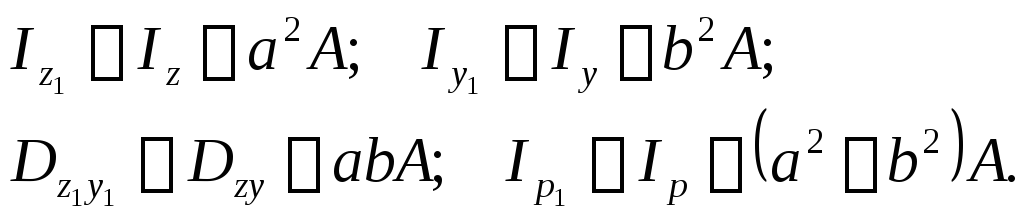
Из полученных формул видно, что моменты инерции относительно центральных осей (когда ) имеют наименьшие значения по сравнению с моментами инерции относительно любых других параллельных осей.

3.4. Главные оси и главные моменты инерции

При повороте осей на угол α центробежный момент инерции становится равным

.

Определим положение главных главных осей инерции u, v относительно которых

,

где α₀ – угол, на который надо развернуть оси y и z, чтобы они стали главными.

Поскольку формула дает два значения углаи, то существуют две взаимно перпендикулярные главные оси. Ось максимума всегда составляет меньший угол () с той из осей (z или y), относительно которой осевой момент инерции имеет большее значение. Напомним, что положительные углы откладываются от оси z против хода часовой стрелки.

Моменты инерции относительно главных осей называются главными моментами инерции. Можно показать, что они

.

Знак плюс перед вторым слагаемым относится к максимальному моменту инерции, знак минус – к минимальному.