
- •Санкт-Петербургский национальный исследовательский университет
- •Редакторы знаний и функции системы kappa
- •Основные этапы разработки объектной модели
- •Пример. Окно Object Browser
- •Построение функциональной модели с использованием продукционных правил Цикл формирования цепи рассуждений в прямом направлении
- •If посылка then заключение.
- •Формирование цепи рассуждений в обратном направлении
- •Средства отладки базы знаний
- •Окно связи правил (Rule Relations)
- •Окно трассировки правил (Rule Trace)
- •Активная трассировка при прямом формировании цепочки рассуждений
- •Окно просмотра иерархии выводов (Inference Browser)
- •Средства создания интерфейса с пользователем. Окно сеанса (Session Window)
- •Средства объяснений оболочки kappa
- •Практическое задание
- •Разработка и программирование объектной модели предметной области
- •Разработка и программирование функциональной модели предметной области
- •Компьютерный практикум по нечетким системам
- •Аппроксимация функции одной переменной с использованием нечеткой системы
- •Варианты заданий
- •Построение элементарной нечеткой экспертной системы
- •Программирование нечеткой системы в среде matlab с использованием встроенных функций
- •Кластеризация с помощью алгоритма нечетких центров
- •Компьютерный практикум по нейронным сетям
- •Аппроксимация функции на основе нейронных сетей
- •Варианты заданий
- •Использование инструмента nnTool для построения нейронной сети
- •Кластеризация с помощью нейронных сетей
- •Рекуррентные нейронные сети Хопфилда и Хэмминга
- •Нейронные сети радиально-базисных функций. Вероятностные сети
- •Построение нейронечеткой модели с помощью anfis-редактора
- •Приложение 1. Функции пакета «Fuzzy Logic Toolbox» системы matlab для работы с системами нечеткой логики
- •Приложение 2. Функции пакета «Neural Network Toolbox» системы matlab для работы с нейронными сетями
Кластеризация с помощью алгоритма нечетких центров
Цель: Освоить методику нахождения центров кластеров.
Задание: Найти центры кластеров, используя алгоритм нечетких центров с помощью программы Clustering (Кластеризация), входящий в пакет Fuzzy Logic Toolbox математической среды MATLAB.
Основные теоретические сведения [45]:
Кластеризация – это объединение объектов в группы (кластеры) на основе схожести признаков для объектов одной группы и отличий между группами. Кластер (от английского cluster) – гроздь, пучок, скопление, группа элементов, характеризуемых каким-либо общим свойством.
Кластеризация помогает представить неоднородные данные в более наглядном виде и для дальнейшего, более удобного, использования этих данных.
Кластеризация может быть использована для решения следующих задач:
обработка изображений;
классификация;
тематический анализ коллекций документов;
построение репрезентативной выборки.
Кластерный анализ предназначен для разбиения множества объектов на заданное или неизвестное число классов на основании некоторого математического критерия качества классификации. Критерий качества кластеризации в той или иной мере отражает следующие неформальные требования:
внутри групп объекты должны быть тесно связаны между собой;
объекты разных групп должны быть далеки друг от друга.
Эти требования выражают стандартную концепцию компактности классов разбиения. Узловым моментом в кластерном анализе считается выбор меры близости объектов (метрики), от которого решающим образом зависит окончательный вариант разбиения объектов на группы при заданном алгоритме разбиения. В каждой конкретной задаче этот выбор производится по-своему, с учетом главных целей исследования, физической и статистической природы используемой информации и т.д.
В кластерном анализе так же важно расстояние между целыми группами объектов. Приведем примеры наиболее распространенных расстояний и мер близости, характеризующих взаимное расположение отдельных групп объектов.
Пусть:
![]() –i-я
группа (класс, кластер) объектов;
–i-я
группа (класс, кластер) объектов;
Ni
– число объектов, образующих группу
![]() ,
каждый объект представляет собой точку
в n-мерном
пространстве;
,
каждый объект представляет собой точку
в n-мерном
пространстве;
i
– среднее арифметическое объектов,
входящих в
![]() (т.е.i
– «центр тяжести» i-й
группы);
(т.е.i
– «центр тяжести» i-й
группы);
p – число групп (кластеров);
![]() –i-й
объект кластера;
–i-й
объект кластера;
q
(
![]() )
– расстояние между группами
)
– расстояние между группами
![]() и
и![]() .
.
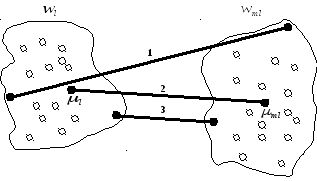
Рис.
4.23. Различные способы определения
расстояния между кластерами
![]() и
и
![]() :
1 – по самым далеким объектам , 2 – по
центрам тяжести, 3 – по ближайшим
объектам
:
1 – по самым далеким объектам , 2 – по
центрам тяжести, 3 – по ближайшим
объектам
Расстояние ближайшего соседа есть расстояние между ближайшими объектами кластеров (рис. 4.23):
![]() .
.
Расстояние дальнего соседа – расстояние между самыми дальними объектами кластеров (рис. 5.23):
![]() .
.
Расстояние центров тяжести равно расстоянию между центральными точками кластеров (рис. 4.23):
![]()
Выбор той или иной меры расстояния между кластерами влияет на вид выделяемых алгоритмами кластерного анализа геометрических группировок объектов в пространстве признаков. Так, алгоритмы, основанные на расстоянии ближайшего соседа, хорошо работают в случае группировок, имеющих сложную, в частности, цепочечную структуру. Расстояние дальнего соседа применяется, когда искомые группировки образуют в пространстве признаков шаровидные облака. И промежуточное место занимают алгоритмы, использующие расстояния центров тяжести и средней связи, которые лучше всего работают в случае группировок эллипсоидной формы.
Алгоритмы кластерного анализа отличаются большим разнообразием. Это могут быть, например, алгоритмы, реализующие полный перебор сочетаний объектов или осуществляющие случайные разбиения множества объектов. В то же время большинство таких алгоритмов состоит из двух этапов:
на первом этапе задается начальное (возможно, искусственное или даже произвольное) разбиение множества объектов на классы и определяется некоторый математический критерий качества автоматической классификации;
на втором этапе объекты переносятся из класса в класс до тех пор, пока значение критерия не перестанет улучшаться.
Таким образом, алгоритмы кластеризации основаны на подобии образов и размещают близкие образы в один кластер.
Выявление центров – это значимый этап при предварительной обработке данных, так как он позволяет сопоставить с этими центрами функции принадлежности переменных при проектировании системы нечеткого вывода.
Программа Clustering (Кластеризация) пакета Fuzzy Logic Toolbox математической среды MATLAB выявляет центры кластеров, т.е. точки в многомерном пространстве данных, около которых группируются (скапливаются) экспериментальные данные.
В программе Clustering (Кластеризация) используются два алгоритма выявления центров кластеров: Subtractive clustering (вычитающая кластеризация) и Fuzzy c-means (алгоритм нечетких центров).
В основе первого алгоритма лежит предложение, что каждая экспериментальная точка может быть центром кластера, при этом вначале для каждой точки вычисляется мера правдоподобия данного предположения («потенциал точки»), основанная на плотности точек в заданной окрестности рассматриваемой. Дальнейшие вычисления происходят итеративно:
точка с наибольшим потенциалом объявляется центром первого кластера;
из отмеченной окрестности этой точки удаляются все остальные точки;
из оставшихся точек объявляется центр следующего кластера и т.д., пока не будут рассмотрены (исключены или объявлены центрами) все точки.
Алгоритм Fuzzy c-means является более точным, для его работы требуется задание таких опций, как число кластеров и число итераций. Рассмотрим его более подробно.
Кластеризация на основе алгоритма нечетких центров. На основе нечеткого c-means алгоритма выполняется кластеризация данных. Этот алгоритм кластеризации предложил Джеймс Бэздэк (James Bezdek) в 1981 году.
Существует множество методов кластеризации, которые можно классифицировать на четкие и нечеткие. Четкие методы кластеризации разбивают исходное множество объектов X на несколько непересекающихся подмножеств. При этом любой объект из X принадлежит только одному кластеру. Нечеткие методы кластеризации позволяют одному и тому же объекту принадлежать одновременно нескольким (или даже всем) кластерам, но с различной степенью истинности. Нечеткая кластеризация во многих ситуациях более «естественна», чем четкая, например, для объектов, расположенных на границе кластеров.
Задача нечеткой кластеризации ставится следующим образом:
Дано:
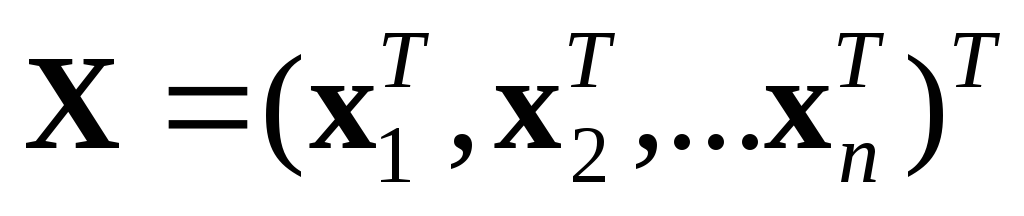 –объекты, подлежащие
кластеризации, где n – количество
объектов,
–объекты, подлежащие
кластеризации, где n – количество
объектов,
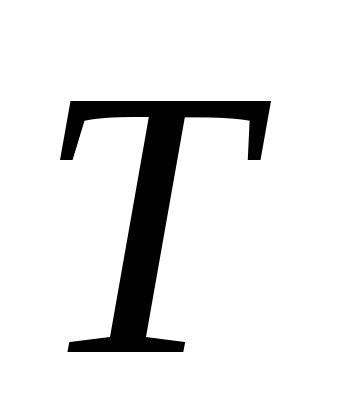 – символ транспонирования. Каждый
объект
– символ транспонирования. Каждый
объект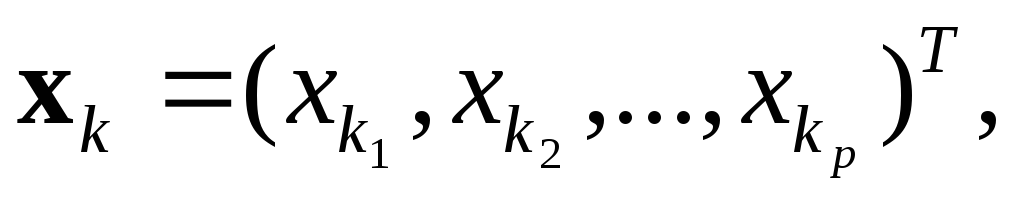
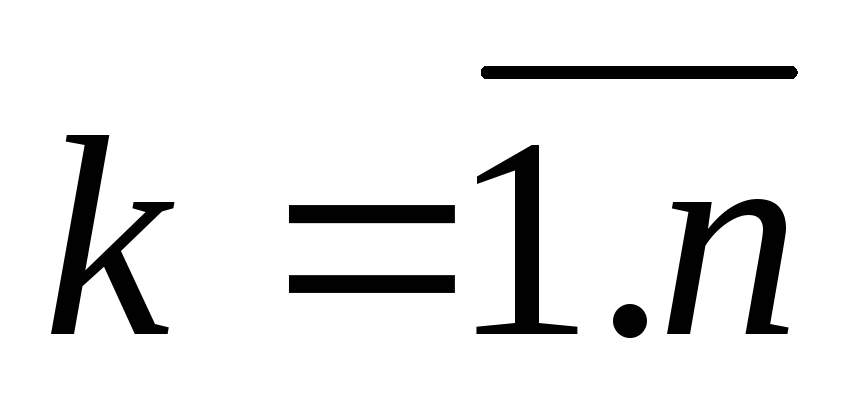 представляет собой точку в p-мерном
пространстве признаков;
представляет собой точку в p-мерном
пространстве признаков;c – количество кластеров (
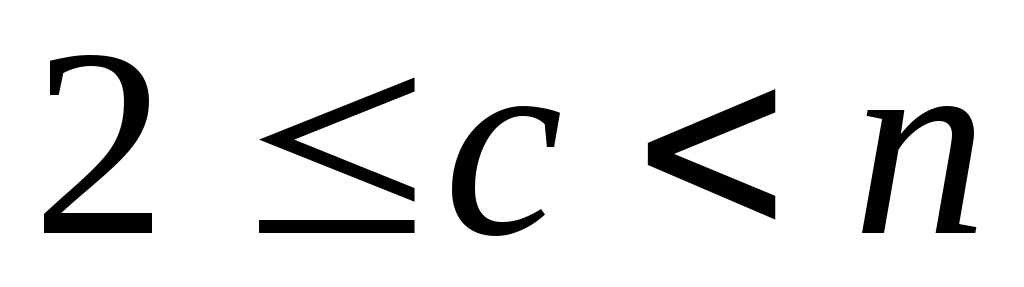 ).
).
Необходимо каждому
элементу множества
![]() поставить в соответствие степени
принадлежности к классам.
поставить в соответствие степени
принадлежности к классам.
Элементы одного
кластера должны быть так близки друг к
другу, как это только возможно, и,
одновременно, кластеры должны быть на
наибольшем удалении друг от друга. Для
обеспечения управляемости процесса
кластеризации необходимо использовать
меру близости, в качестве которой обычно
определяют расстояние между двумя
объектами (точками в p-мерном
пространстве)
![]() и
и![]() в виде вещественной функции
в виде вещественной функции![]() такой что:
такой что:
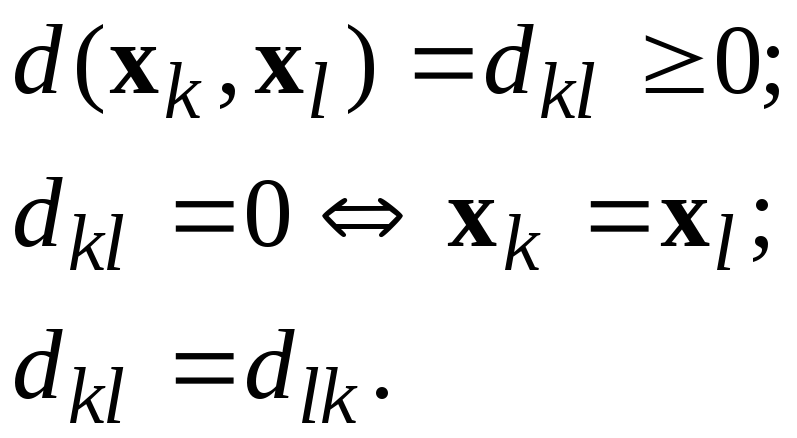
Дополнительно,
если функция
![]() удовлетворяет правилу треугольника,
т.е.
удовлетворяет правилу треугольника,
т.е.![]() ,
тогда эта функция является метрикой,
хотя выполнение этого свойства не всегда
необходимо для задач кластеризации.
,
тогда эта функция является метрикой,
хотя выполнение этого свойства не всегда
необходимо для задач кластеризации.
Любое разбиение
множества
![]() на нечеткие подмножестваSi
(
на нечеткие подмножестваSi
(![]() )
может быть полностью описано функцией
принадлежности
)
может быть полностью описано функцией
принадлежности![]()
Обозначим через
![]() –
степень принадлежности объекта
–
степень принадлежности объекта![]() к подмножествуSi,
т.е.
к подмножествуSi,
т.е.
![]() ,
а через
,
а через![]() – множество
всех действительных матриц размером
– множество
всех действительных матриц размером
![]() .
Тогда нечеткимс-разбиением
(или матрицей степеней принадлежности)
называется матрица
.
Тогда нечеткимс-разбиением
(или матрицей степеней принадлежности)
называется матрица
![]() при выполнении следующих условий:
при выполнении следующих условий:
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
![]() (4.3)
(4.3)
В отличие от четкого, при нечетком c-разбиении любой объект одновременно принадлежит к различным кластерам, но с разной степенью. Условия (4.2) и (4.3) требует только, чтобы сумма степеней принадлежности объекта ко всем кластерам была нормализована к 1, а также чтобы количество кластеров, к которым принадлежит объект не превышало c.
Обозначим центры
кластеров, т.е. точки в р-мерном
пространстве, вокруг которых
сконцентрированы соответствующие
объекты, через
![]() ,
,![]()
При использовании
евклидового расстояния задача нечеткой
кластеризации состоит в нахождении
такой матрицы степеней принадлежности
M
и таких координат центров кластеров
![]() ,
которые обеспечивают минимум следующего
критерия:
,
которые обеспечивают минимум следующего
критерия:
![]() ,
,
где
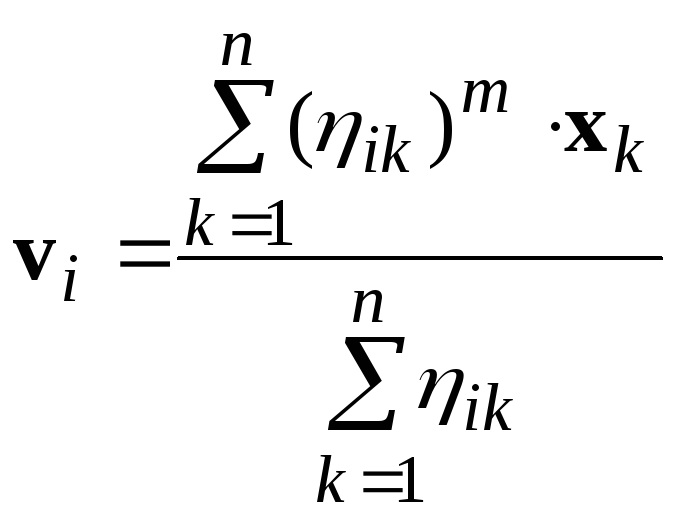 – центрi-го
кластера,
– центрi-го
кластера,
![]() ,m
– так называемый экспоненциальный вес
(
,m
– так называемый экспоненциальный вес
(![]() ).
В математике под обозначением
).
В математике под обозначением![]() обычно понимают норму, т.е. функцию,
заданную на векторном пространстве и
обобщающая понятие длины вектора.
обычно понимают норму, т.е. функцию,
заданную на векторном пространстве и
обобщающая понятие длины вектора.
Значение
экспоненциального веса устанавливается
до начала кластеризации. Экспоненциальный
вес m
влияет на матрицу степеней принадлежности
M.
Чем больше m,
тем конечная матрица c-разбиения
становится более «размазанной», а при
![]() все объекты принадлежат всем кластерам
с одинаковой степенью принадлежности,
что является очень плохим решением.
Экспоненциальный вес позволяет также
при формировании координат центров
кластеров усилить влияние объектов с
большими значениями степеней принадлежности
и уменьшить влияние объектов с малыми
значениями степеней принадлежности.
На настоящий момент не существует
теоретически обоснованного правила
выбора значенияm.
Обычно устанавливают m=2.
все объекты принадлежат всем кластерам
с одинаковой степенью принадлежности,
что является очень плохим решением.
Экспоненциальный вес позволяет также
при формировании координат центров
кластеров усилить влияние объектов с
большими значениями степеней принадлежности
и уменьшить влияние объектов с малыми
значениями степеней принадлежности.
На настоящий момент не существует
теоретически обоснованного правила
выбора значенияm.
Обычно устанавливают m=2.
Аналитического решения задачи нахождения оптимальных координат центров кластеров и матрицы степеней принадлежности не существует, поэтому она решается численно. В среде MATLAB алгоритм нечетких центров реализован в функции fcm.
Функция fcm может иметь три входных аргумента:
Х – матрица, представляющая данные, подлежащие кластеризации. Каждая строка матрицы соответствует одному объекту (образу);
с – количество кластеров, которое должно быть получено в результате выполнения функции fcm. Количество кластеров должно быть больше 1 и меньше числа образов, заданных матрицей Х.
options – необязательный аргумент, устанавливающий параметры алгоритма кластеризации:
options(1) – значение экспоненциального веса (по умолчанию – 2.0);
options(2) – максимальное количество итераций алгоритма кластеризации (значение по умолчанию - 100);
options(3) – минимально допустимое значение улучшения целевой функции за одну итерацию алгоритма (значение по умолчанию – 0.000001);
options(4) – вывод промежуточных результатов во время работы функции fcm (значение по умолчанию – 1).
Для использования значений по умолчанию можно ввести NaN в качестве значения соответствующей координаты вектора options.
Алгоритм кластеризации останавливается, когда выполнено максимальное количество итераций или когда улучшение целевой функции за одну итерацию меньше указанного минимально допустимого значения.
Функция fcm имеет три выходных аргумента:
V – матрица координат центров кластеров, полученных в результате кластеризации. Каждая строка матрицы соответствует центру одного кластера;
M – матрица степеней принадлежности образов к кластерам. Каждая строка матрицы соответствует функции принадлежности одного кластера;
obj_fcn – вектор значений целевой функции на каждой итерации алгоритма кластеризации.
Модуль графического интерфейса Findcluster:
GUI-модуль (Модуль графического интерфейса) Findcluster позволяет автоматически находить центры кластеров многомерных данных с помощью нечеткого c-means алгоритма и алгоритма вычитающей кластеризации (subtractive clustering). Загрузка модуля Findcluster осуществляется по команде findcluster. Основное графическое окно модуля Findcluster с указанием назначения функциональных областей приведено на рис. 4.24.
Модуль Findcluster содержит 7 верхних типовых меню графического окна (File (Файл), Edit (Редактирование), View (Обзор), Insert (Вставка), Tools (Инструменты), Windows (Окна) и Help (Помощь)), область визуализации, область загрузки данных, область кластеризации, область вывода текущей информации а также кнопки Info (Информация) и Close (Закрыть), которые позволяют вызвать окно справки и закрыть модуль, соответственно.
Область визуализации
В этой области в
двумерном пространстве выводятся
экспериментальные данные (образы) и
найденные центры кластеров. Для образов
используется маркер в виде красной
окружности (o),
а для центров кластеров – маркер в
виде черной точки (![]() ).
).
В области также расположены меню выбора координатных осей X-axis и Y-axis, позволяющие ассоциировать признаки образов с осями абсцисс и ординат.
Область загрузки данных
В этой области, которая расположена в правом верхнем углу окна, находится кнопка Load Data (Загрузка данных). Нажатие этой кнопки позволяет загрузить данные для кластеризации, хранящиеся на диске. После нажатия кнопки Load Data… открывается типовое окно открытия файла. В файле данные должны быть записаны построчно, т. е. каждому образу должна соответствовать одна строка файла данных.
Область вывода текущей информации
В этой области, которая расположена внизу графического окна, выводится наиболее важная текущая информация, например, состояние модуля, номер итерации алгоритма кластеризации, значение целевой функции и т.п.
Область кластеризации
В этой области пользователь может выбрать алгоритм кластеризации, установить параметры алгоритма кластеризации, провести кластеризацию и сохранить координаты центров кластеров в виде файла. В области расположены следующие меню и кнопки.
Меню Method (Метод) позволяет выбрать один из двух алгоритмов кластеризации: subtractiv – алгоритм вычитающей кластеризации; fcm - нечеткий c-means алгоритм. При выборе алгоритма вычитающей кластеризации графическое окно модуля Findcluster имеет вид, показанный на рис. 4.24. В этом случае пользователь имеет возможность установить значения следующих параметров алгоритма Influence Range (Диапозон влияния), Squash (Давка), Accept Ratio (Принимаемый коэффициент) и Reject Ratio (Отклоненный коэффициент), смысл которых объяснен в описании функции subclust. При выборе нечеткого c-means алгоритма область кластеризации принимает вид, изображенный на рис. 4.25. В этом случае пользователь имеет возможность установить значения следующих параметров: Cluster Num. – количество кластеров; Max Iteration # - максимальное количество итераций алгоритма; Min – минимально допустимое значение улучшения целевой функции за одну итерацию алгоритма; Exponent – значения экспоненциального веса.

Рис. 2.24. Основное окно модуля Findcluster
Рис.
2.26.
Окно выполнения алгоритма вычитающей
кластеризации
Рис.
2.25.
Область кластеризации
Кнопка Start – запускает кластеризацию. При использовании алгоритма fcm значения координат центров кластеров выводятся в окне визуализации после каждой итерации. При использовании вычитающего алгоритма открывается дополнительное окно (рис. 2.26), показывающее динамику процесс кластеризации. Координаты центров кластеров выводятся по окончанию выполнения алгоритма.
Кнопка Clear Plot позволяет очистить поле вывода данных.
Для выявления центров кластеров (точек в многомерном пространстве данных) откроем файл clusterdemo.dat для просмотра его структуры (рис. 2.27). Файл представляет собой массив цифр (экспериментальных данных), сгруппированных в три столбца (многомерный массив).
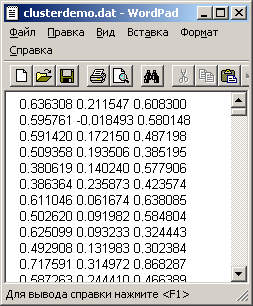
Рис. 2.27. Файл clusterdemo.dat
Пример выполнения:
загрузим файл данных MATLAB\toolbox\fuzzy\fuzdemos\ clusterdemo.dat с помощью кнопки «Load Data»;
выберем алгоритм кластеризации Fuzzy c-means (fcm), с помощью кнопки «Method»;
зададим число кластеров равное 3, с помощью кнопки опции «Cluster num»;
зададим число итераций равное 100, с помощью кнопки опции «Max Iteration#»;
нажимаем кнопку Start и получаем результат (рис. 2.28).
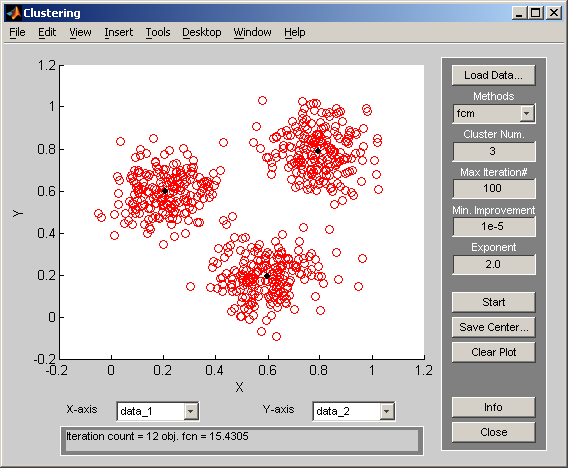
Рис. 2.28. Результат работы программы Clustering
(центры кластеров окрашены в черный цвет).
При увеличении количества кластеров до 30 получим результат, представленный на рис. 2.29.
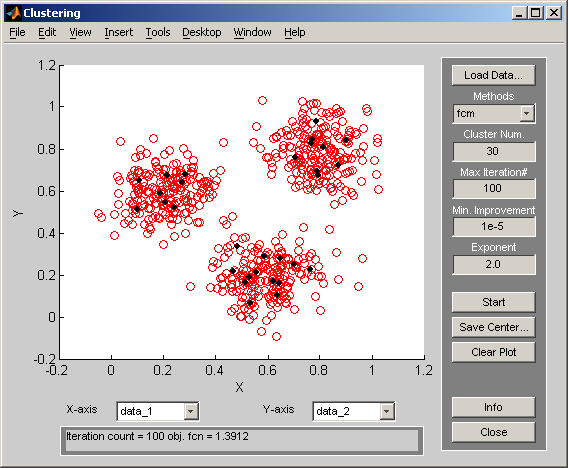
Рис. 2.29. Результат работы программы Clustering
(центры кластеров окрашены в черный цвет).
Выводы (пример):
В результате выполнения лабораторной работы мы ознакомились с графической средой программы кластеризации – Clustering, пакета Fuzzy Logic Toolbox, которая выявляет центры кластеров. Мы убедились, что с помощью этой программы можно быстро найти центры кластеров.
С использованием демонстрационного примера было произведено сравнение работы двух алгоритмов нахождения центров кластеров (алгоритм вычитающей кластеризации и алгоритм нечетких центров). В результате сравнения было выявлено, что алгоритм вычитающей кластеризации менее точен и подойдет, если не нужна высокая точность кластеризации данных, а алгоритм нечетких центров более точен, его нужно применять, если требуется высокая точность результата. Таким образом, точность решения зависит от выбора алгоритма кластеризации и от формы представления входных данных.
Контрольные вопросы:
Какая программа использовалась для выявления центров кластеров?
Дайте определение кластеризации.
Для каких задач может быть использована кластеризация?
Как может быть определено расстояние между кластерами?
Назовите этапы алгоритма кластерного анализа.
Каким образом определяются центры кластеров?
