
Математическое моделирование / Arz_(2010)_Mathematical_&_Computer_Modelling
.pdf– определение погрешности расчетов по математической модели (рис. 1.2, Б); при этом пользователь должен задать величину допустимой погрешности зад исходя из условий задачи, решаемой с помощью математической модели;
– определение значения критерия Фишера (рис. 1.2, В); этот способ очень похож на предыдущий, однако принимает во внимание не только значение невязки (см. рис. 1.3), но и число степеней свободы, используемых для настройки математической модели.
Параметрическая идентификация математической мо-
дели предполагает определение ее вектора параметров (коэффициентов), при которых она в наилучшей степени соответствует реальному объекту. Для решения задачи параметрической идентификации обычно пользуются минимизацией функционала определенного вида, показанного на рис. 1.3. В качестве методов решения задач параметрической идентификации используют методы нелинейного программирования.
Структурная идентификация математической модели
предполагает определение структуры связей между векторами входных и выходных координат (рис. 1.1). При решении данной задачи могут быть использованы методы корреляционного анализа.
По своей сути данная проблема весьма похожа на задачу об идентификации структуры «черного ящика», лишь на основе информации о его входах и выходах. Существует два принципиальных подхода к структурной идентификации объекта: конструктивный и деструктивный. При конструктивном подходе обычно следуют от некоторой «минимальной» структуры по пути ее постепенного наращивания; такой процесс продолжается до тех пор, когда структурные возможности модели не начинают удовлетворять исследователя. При деструктивном подходе выбирается некоторая избыточная структура, которая в дальнейшем упрощается до тех пор, пока такое упрощение не приводит к структурным изменениям в объекте моделирования.
20

Рис. 1.2. Различные способы проверки адекватности математической модели
Рис. 1.3. Сравнение модели и объекта
21

1.2. Сферы применения математического и компьютерного моделирования
Основные области применения математического и компьютерного моделирования приведены в табл. 1.1.
Таблица 1.1
Основные сферы применения математического и компьютерного моделирования
Наука |
|
Образование |
|
Техника |
|
Искусство |
Общественная |
|||||||
|
и технологии |
|
жизнь |
|
||||||||||
Исследование |
Проведение |
Проектирова- |
|
Компьютер- |
Изучение |
обще- |
||||||||
свойств объектов |
вычислитель- |
ние |
новых |
ная графика и |
ственного |
мне- |
||||||||
в биологии, фи- |
ных |
экспери- |
технологий, |
|
анимация; |
ния; |
создание |
|||||||
зике, |
химии и |
ментов |
в |
раз- |
материалов, |
|
семантиче- |
адекватных |
мо- |
|||||
других |
естест- |
личных |
облас- |
аппаратуры, |
|
ские модели |
делей |
«среднего |
||||||
венных |
науках; |
тях |
естествен- |
приборов |
|
|
человека», |
изу- |
||||||
временное |
про- |
ных |
наук, а |
и т. п. (САПР); |
|
чение |
его |
реак- |
||||||
гнозирование; |
также социаль- |
управление |
|
|
ций |
на |
те |
или |
||||||
предсказание |
ных, |
психоло- |
объектами; |
|
|
иные |
управлен- |
|||||||
новых |
свойств, |
гических |
и |
искусственный |
|
ческие решения; |
||||||||
эффектов, |
зако- |
педагогических |
интеллект |
и |
|
политические |
||||||||
номерностей |
и |
системах |
с |
распознавание |
|
технологии |
и |
|||||||
условий их |
воз- |
целью |
изуче- |
образов |
|
|
управление |
об- |
||||||
никновения; |
|
ния |
той |
или |
|
|
|
|
щественным |
|||||
автоматизиро- |
иной |
предмет- |
|
|
|
|
мнением |
|
|
|||||
ванный |
экспери- |
ной |
области, |
|
|
|
|
|
|
|
|
|||
мент; |
обработка |
профессио- |
|
|
|
|
|
|
|
|
|
|||
результатов |
экс- |
нального |
тре- |
|
|
|
|
|
|
|
|
|||
периментов; |
|
нинга и т. д. |
|
|
|
|
|
|
|
|
||||
измерительные |
|
|
|
|
|
|
|
|
|
|
|
|
||
комплексы и др. |
|
|
|
|
|
|
|
|
|
|
|
|
||
1.3. Основныепринципыматематическогомоделирования1
Принцип информационной достаточности. При полном отсутствии информации об исследуемой системе построение ее модели невозможно. При наличии полной информации о системе ее моделирование лишено смысла. Поэтому существует не-
1 Гультяев А. Визуальное моделирование в среде MATLAB. – СПб.: Пи-
тер, 2000.
22

который критический уровень априорных сведений о системе (уровень информационной достаточности), при достижении которого может быть построена ее адекватная модель. Сама возможность такого построения зависит от используемого математического аппарата, моделируемой системы и в известном смысле от интуиции и опыта человека или коллектива, разрабатывающего такую модель. В некоторых случаях удается построить адекватную модель в случае, когда для ее параметрической идентификации используется лишь незначительная часть данных генеральной совокупности. Например, при разработке одной из моделей на основе аппарата искусственных нейронных сетей нами было использовано лишь 9,454 10–17 части генеральной совокупности данных. При этом погрешность модели составила приблизительно 5 %!1
Принцип осуществимости. Создаваемая модель должна обеспечивать достижение поставленной цели исследования с заданной вероятностью и за конечное время. Обычно задают некоторое пороговое значение P0 – вероятности достижения цели моделирования P(t), а также приемлемую границу t0, времени достижения этой цели. Модель считают осуществимой, если может быть выполнено условие P (t0) ≥ P0.
Принцип множественности моделей. Данный принцип яв-
ляется ключевым. Речь идет о том, что создаваемая модель должна отражать в первую очередь те свойства реальной системы (или явления), которые влияют на выбранный показатель эффективности. Соответственно при использовании любой конкретной модели познаются лишь некоторые стороны реальности. Для более полного ее исследования необходим ряд моделей, позволяющих с разных сторон и с разной степенью детальности отражать рассматриваемый процесс.
1 Арзамасцев А. А., Зенкова Н. А. Моделирование психологического теста с помощью аппарата искусственных нейронных сетей // Вестник ТГУ. – 2005. – Т. 10. – Вып. 2. С. 176-183; Арзамасцев А. А., Зенкова Н. А., Неудахин А. В. Моделирование в психологических, социальных и медицинских системах с использованием методов искусственного интеллекта // Вестник ТГУ. – 2009. – Т. 14. – Вып. 5. С. 995-1012.
23
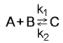
Принцип агрегирования. В большинстве случаев сложную систему можно представить состоящей из агрегатов (подсистем), для адекватного математического описания которых оказываются пригодными некоторые стандартные математические схемы. Принцип агрегирования позволяет, кроме того, достаточно гибко перестраивать модель в зависимости от задач исследования.
Принцип параметризации. В ряде случаев моделируемая система имеет в своем составе некоторые относительно изолированные подсистемы, характеризующиеся определенным параметром, в том числе векторным. Такие подсистемы возможно заменять в модели соответствующими числовыми величинами, а не описывать процесс их функционирования. При необходимости зависимость значений этих величин от ситуации может задаваться в виде таблицы, графика или аналитического выражения (формулы). Принцип параметризации позволяет сократить объем и продолжительность моделирования. Однако надо иметь в виду, что параметризация снижает адекватность модели.
1.4. Классификация математических моделей
Все многообразие моделей (и объектов) можно разделить на несколько больших классов (рис. 1.4). В зависимости от этой классификации происходит выбор подходящего математического аппарата, т. е. вида уравнения (1.1) пользователем.
Так, в зависимости от участия или неучастия в (1.1) фактора времени математические модели подразделяются на модели ди-
намики и модели статики.
Приведем следующий пример. Пусть имеется некоторая бимолекулярная гомогенная реакция вида:
(1.2)
24
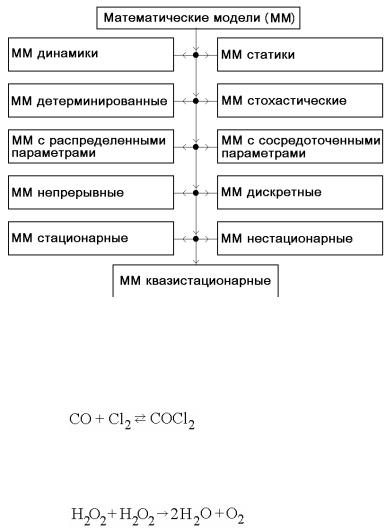
Рис. 1.4. Классификация математических моделей
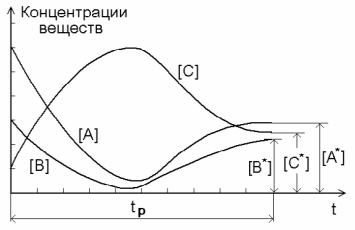
В качестве таких реакций могут выступать, например, взаимодействие моноокиси углерода и хлора с образованием фосгена:
(1.3)
или реакция гидролиза ацетилхолина и разложения пероксида водорода по уравнению:
(1.4)
Требуется привести математические модели динамики и статики этого процесса. Будем использовать закон действующих масс, согласно которому скорость химического взаимодействия пропорциональна концентрациям взаимодействующих агентов.
25
В соответствии с этим можно записать следующие дифференциальные уравнения для математической модели реакции (1.2):
d[A] |
= −k [A][B] + k |
[C] |
|
||||
|
|
||||||
dt |
|
1 |
2 |
|
|
||
|
|
|
|
|
|||
d[B] |
= −k1[A][B] + k2 |
[C] |
(1.5) |
||||
dt |
|||||||
|
|
|
|
|
|||
d[C] |
= k [A][B] − k |
[C] |
|
||||
|
|
||||||
dt |
1 |
2 |
|
|
|
||
|
|
|
|
|
|||
Здесь [A], [B], [С] обозначают концентрации веществ A, B, С. Данная система дифференциальных уравнений должна быть дополнена начальными условиями вида: [A(t0)] = [A0]; [В(t0)] = [В0]; [С(t0)] = [С0], которые задают концентрации реагирующих веществ в начальный момент времени t0.
На рис. 1.5 показаны графики зависимостей концентраций от времени, в соответствие с математической моделью (1.5). Такая модель, учитывающая изменение концентраций во времени называется моделью динамики, а зависимости, показанные на рис. 1.5 – динамическими кривыми, динамическими характеристиками и т. д.
Из этого рисунка видно, что по истечению некоторого времени производные d [A]/dt = d [B]/dt = d [C]/dt = 0 становятся равными нулю, так что:
−k1[A][B] + k2 [C] = 0 |
|
−k1[A][B] + k2 [C] = 0 |
(1.6) |
k1[A][B] −k2 [C] = 0 |
|
Решением алгебраической системы уравнений (1.6) являются некоторые значения [A*], [B*], [C*], в которые приходит система по истечению значительного времени. Модель (1.6) называется моделью статики. Она характеризует значения концен-
26
траций в установившемся процессе, для которого t→∞. В реальных случаях выход объекта на статический режим наблюдается обычно за достаточно большое, но не бесконечное время. Так, для рис. 1.5 в качестве такого времени может быть выбрано время завершения химической реакции tp.
Таким образом, можно сделать следующие выводы:
–модель динамики объекта переходит в модель статики этого же объекта, если устремить время к бесконечности; при существовании устойчивых решений значения производных при этом стремятся к нулю;
–время обычно не присутствует в моделях статики в явном виде; исключение составляют нестационарные модели, в которых могут существовать временные зависимости физических, геометрических и иных параметров модели;
–в качестве математических аппаратов для реализации моделей динамики часто используют обыкновенные дифференциальные уравнения (для объектов с сосредоточенными параметрами), дифференциальные уравнения в частных производных (для объектов с распределенными параметрами), соответствующие разностные схемы.
Рис. 1.5. Графики изменения концентраций реагентов A, B, С бимолекулярной реакции
27
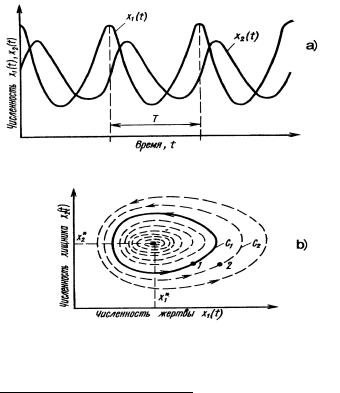
Внекоторых случаях, статических режимов в «чистом виде» не наблюдается вовсе, т. к. на выходе системы наблюдаются периодические колебания. Например, в известной модели Лот- ки-Вольтерра наблюдаются автоколебания численности хищников и жертв (рис. 1.6).
Взависимости от степени участия или неучастия в (1.1) случайного фактора математические модели подразделяются на модели детерминированные и стохастические.
Особенностью детерминированных моделей является полная воспроизводимость (повторяемость) вычислительного эксперимента в идентичных условиях. При использовании стохастических моделей можно говорить о воспроизводимости вычислительного эксперимента лишь в статистическом плане.
Рис. 1.6. Динамические характеристики – a) и фазовый портрет – b) математической модели Лотки – Вольтера, характеризующей взаимодействия в системе «хищник»–«жертвы»1
1 ФедоровВ. Д., ГильмановТ. Г. Экология. – М.: Изд-воМГУ, 1980. – 464 с.
28
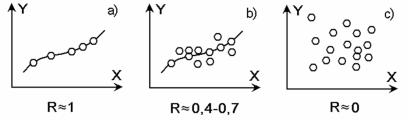
Отличие детерминированных и стохастических объектов хорошо видно из анализа их статических характеристик. Так, на рис. 1.7. показаны такие характеристики. Здесь же приведены значения коэффициентов корреляций между факторами x и y, характерные для указанных случаев.
Математическая модель (1.6) из предыдущего примера является детерминированной на том основании, что ее решение зависит лишь от начальных концентраций реагентов и констант реакции, т. е. при одинаковых начальных условиях будем иметь абсолютно одинаковые концентрации на выходе модели.
Во многих случаях использование детерминированных моделей не дает положительных результатов, т. к. сам процесс не является определенным. Примерами таких процессов являются, броуновской движение (физика), взаимодействие молекул (химия), поиск партнера животными (биология). Для описания подобных процессов часто используют аппарат теории вероятности, в частности функции плотности распределения случайных величин и функции их распределений, основные свойства которых представлены на рис. 1.8.
В зависимости от степени пространственной протяженности объекта математические модели могут быть с распределенны-
ми или сосредоточенными параметрами.
Так, например, возможны различные способы представления объекта, схематично представленного на рис. 1.9.
Рис. 1.7. a) – полностью детерминированный объект; b) – частично «зашумленный» объект; шум может быть связан как со случайной природой самого объекта, так и с наличием ненаблюдаемых факторов или ошибок измерения; c) – полностью стохастический объект. R – коэффициент корреляции
29
