
Математическое моделирование / Arz_(2010)_Mathematical_&_Computer_Modelling
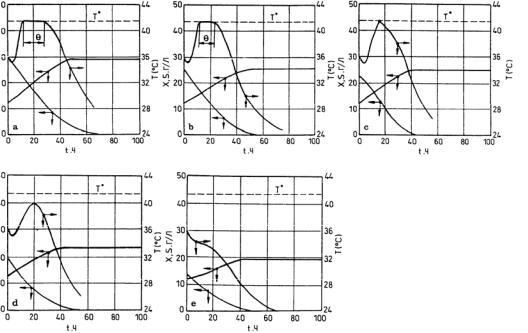
.pdfсаморегулирования становится равным нулю, т. е. процесс выходит из этого состояния, едва успев в него попасть (рис. 2.30, с). Такое состояние в рассматриваемом процессе наблюдается при So = 22,5 г/л. При дальнейшем уменьшении So система «не успевает» выйти на режим саморегулирования, хотя тенденция к Т* и в этих случаях имеется (рис. 2.30, d, e).
Отсюда можно сделать заключение, что поскольку саморегулирование температуры в биореакторе возможно далеко не всегда, нахождение условий существования явления представляет собой самостоятельную задачу.
Условие входа в режим саморегулирования в общем виде сформулировать довольно трудно, т. к. в этом случае сущест-
венное влияние оказывают параметры Θ, μ'0, То, So, Text. А вот выход из режима наблюдается, когда концентрации S и Х станут
такими, что будет выполняться неравенство:
SX |
< |
kP(T * −T |
) |
|
|
ext |
|
(2.76) |
|
S + KS |
μmVH |
|
||
|
|
|
где μm представляет собой эффективную удельную скоростьроста
микроорганизмов впериод саморегулирования температуры.
На рис. 2.31 показаны фазовые траектории процесса в координатах Х–S–T. Заштрихованная область в плоскости Х–S, а также все точки фазового пространства, находящиеся над ней, соответствуют невозможности саморегулирования. В других точках пространства явление возможно. Эффект саморегулирования исчезает, как только фазовая траектория проходит через границу области, определяемую уравнением (2.76): точки А, В, С на рис. 2.31. Границы области, как это следует из (2.76), являются свойством системы реакций, самого реактора и внешней среды и могут смещаться в плоскости Х–S с изменением последних.
Из уравнений (2.70) и (2.73) следует еще один важный вы-
вод. Если Тext = Т*, то dX/dt = O, т. е. ход процесса полностью прекращаeтся в результате невозможности передачи тепла через
стенку реактора.
90
а) |
b) |
c) |
d) |
e) |
Рис. 2.30. Саморегулирование температуры в периодическом режиме при различных начальных концентрациях субстрата: a) – 30 г/л; b) – 25 г/л; c) – 22.5 г/л; d) – 20 г/л; e) – 12.5 г/л; a)–c) демонстрируют область саморегулирования температуры; d) и e) – саморегулирование отсутствует
91
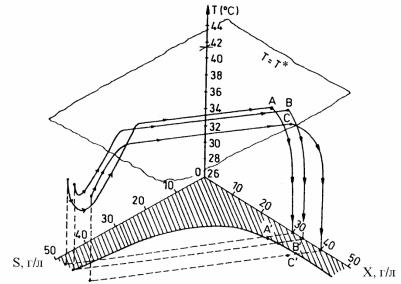
Рис. 2.31. Фазовыетраекториипроцесса приразличныхXo: 12, 6 и3 г/л. So = 50 г/л
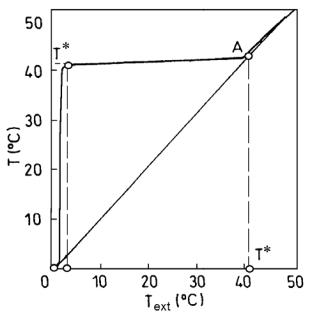
На рис. 2.32 показан качественный характер зависимости температуры в реакторе от температуры снаружи реактора – Тext для непрерывного режима. Несмотря на то, что для различных систем реакций этот график может быть существенно деформирован, характерным для него является наличие зоны с практически нулевой чувствительностью по температурному каналу и точки А, в которой Т = Т* и Тext = Т*. Таким образом, саморегулирование возможно в ограниченном и вполне определенном диапазоне наружных температур от Т1 до Т* (рис. 2.32).
Недостатком математической модели (2.59)–(2.67), выявленным в результате ее тестирования, явился тот факт, что она не описывает один и тот же объект (биохимический реактор) при принудительном термостатировании так, как она это делает в режиме саморегулирования температуры. Кроме этого, она не описывает кинетику потребления кислорода в аэробном процессе, что может оказывать существенное влияние на саморегулирование.
92
Т1
Рис. 2.32. Границы саморегулирования температуры
Несмотря на пользу, полученную от анализа уравнений модели (2.59)–(2.67), указанные недостатки снижает ценность результатов, полученных в данном разделе.
По этой причине далее предпринята попытка разработки математической модели, лишенной отмеченных недостатков.
Модель саморегулирования температуры в реакторе (модель 2)
Система допущений, выбор и обоснование структуры и уравнений. Моделируемый объект представляет собой биохимический реактор, в котором осуществляется рост биомассы в результате ассимиляции и окисления субстрата. Основной процесс проходит в жидкой фазе, однако необходимый для жизнедеятельности микроорганизмов и окисления субстрата кислород поступает из газовой фазы, подаваемой в реактор через диспер-
93
гирующее устройство. Реактор представляет собой емкость с хорошим перемешиванием и имеет входные и выходные патрубки для подачи исходных веществ и отвода продуктов биосинтеза, которые в периодическом режиме закрываются. Такая конструкция является типичной для процессов, проводимых в аэробных условиях.
При разработке математической модели такого объекта примем следующие основные допущения:
–внутри реактора значения концентраций и других факторов являются величинами постоянными по всему объему, т. е. он является объектом с сосредоточенными параметрами;
–рассматриваемая система является полностью закрытой по веществу и открытой по энергии для реактора периодического типа, открытой по веществу и энергии для реактора непрерывного типа;
–макрокинетика ферментативных реакций выражается зависимостью Микаэлиса-Ментен;
–повышение температуры в реакторе сверх супраоптимального значения приводит к обратимому ингибированию ферментной системы;
–в отношении факторов, оказывающих существенное влияние на максимальную удельную скорость ферментативной реакции, справедлива концепция «узкого места»;
–зависимость максимальной удельной скорости роста микроорганизмов от температуры может быть представлена в виде разности двух компонент, каждая из которых подчиняется уравнению Аррениуса;
–суммарный эффект биохимических реакций положительный;
–плотность и удельная теплоемкость среды в реакторе мало меняются в ходе процесса.
Справедливость первых двух допущений очевидна, другие приемлемы для большей части рассматриваемых процессов и обоснованы в предыдущем разделе.
Математическая модель объекта, построенная с учетом приведенных допущений имеет следующий вид:
94

dT |
= μ |
|
XH |
− |
|
kp (T −Text ) |
+ |
Q |
(2.77) |
|||||||
dt |
|
cρ |
|
|
|
cρV |
|
|
||||||||
|
|
|
r |
|
|
|
|
|
|
|
T |
|
||||
dX |
|
= μr X + QX |
|
|
|
|
|
|
(2.78) |
|||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dS |
= |
− |
μr X + QS |
|
|
|
|
|
(2.79) |
|||||||
dt |
|
|
|
|
|
|||||||||||
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
||
d μ′m |
= |
[μm (T )−μ′m |
] |
|
Θ1 |
, d μ′m |
dt≥ 0 |
|
|
(2.80) |
||||||
|
|
[μ |
(T )−μ′ |
] |
|
|
, d μ′ |
|
|
|
||||||
dt |
|
|
Θ2 |
dt< 0 |
|
|
||||||||||
|
|
|
|
|
m |
|
m |
|
|
m |
|
|
|
|||
Уравнения (2.77)–(2.80) аналогичны, соответствующим уравнениям математической модели, представленной в предыдущем разделе. Дополнительно к ним введено уравнение:
dC = K |
a (C * −C) − q |
+ Q . |
(2.81) |
|
dt |
L |
O2 |
C |
|
|
|
|
|
|
Эти уравнения описывают динамику изменения температуры внутри реактора (2.77), концентрации биомассы (2.78), субстрата (2.79) и растворенного кислорода (2.81). Уравнение (2.80) характеризует инерционность ферментной системы. Решать систему (2.77)-(2.81) необходимо с начальными условиями:
T (0) = T0, X (0) = X0, S (0) = S0, μ'm(0)= μ'm0, C (0) = C0. Парамет-
ры уравнений (2.77) – (2.81) можно рассчитать по следующим соотношениям:
μ′ SC |
|
μr = (S + KS m) (C + KC ), |
(2.82) |
95
представляет собой действительную удельную скорость роста биомассы,
qO2 = X (μrβ + a), |
(2.83) |
удельное потребление кислорода в эндогенном и экзогенном процессах,
μm (T) =a1 exp(−E1 / RT) −a2 exp(−E2 / RT) , |
(2.84) |
Y (T ) =1,4765 − 0,02353(T − 273,15) , |
(2.85) |
C* (T ) =14,438 −0,34755 T + |
|
4,6557 10−3 T 2 −2,62965 10−5 T 3 , |
(2.86) |
температурные зависимости для максимальной удельной скорости роста микроорганизмов, экономического коэффициента и концентрации насыщения растворенного кислорода в жидкой фазе. Уравнения (2.85)–(2.86) являются эмпирическими и получены нами в результате аппроксимации экспериментальных данных. Однако характер этих зависимостей мало меняется для различных объектов. Для непрерывного процесса притоки и стоки компонент уравнений (2.77)–(2.79) и (2.81) можно рассчитать по выражениям:
QT = F(Tin −T ) /V = D(Tin −T ) |
(2.87) |
QX = F ( X in − X ) /V = D( Xin − X ) |
(2.88) |
QS = F (Sin − S) /V = D(Sin − S) |
(2.89) |
QC = F (Cin − C) /V = D(Cin − C) . |
(2.90) |
96
Уравнения (2.77)–(2.90) представляют собой замкнутую систему и позволяют проводить расчет временных профилей изменения температуры, концентраций биомассы, субстрата и растворенного кислорода при заданных кинетических и технологических параметрах модели и начальных условиях.
Идентификация математической модели и проверка ее адекватности экспериментальным данным. Параметрическая идентификация модели (2.77)–(2.90) проводилась на основе данных для роста Candida tropicalis на н-алканах. Данные получены из экспериментальных работ других авторов. Модель реализована в виде программы на языке Borland Pascal. Решение системы дифференциальных уравнений (2.77)–(2.81) проводили методом Рунге-Кутта четвертого порядка с постоянным шагом, который выбирали методом двойного пересчета по всей числовой выборке, полученной в расчете. В итоге величина шага была выбрана 0,0002 ч, при максимальной длине временной шкалы в 80 ч. В процессе идентификации использовались поисковые процедуры, написанные автором на языках Borland Pascal, Basic и Eureka Solver, а также встроенные средства систем Eureka Solver и MatLab. Исходная математическая модель именно на этом этапе была дополнена эмпирическими уравнениями (2.85)– (2.86), которые выражают реально имеющиеся, но не являющиеся предметом рассмотрения в данной работе факты: наличие температурных зависимостей экономического коэффициента для биосинтеза и концентрации насыщения для газа, растворенного в жидкости. Указанные действия позволили получить хорошее соответствие расчетов, выполненных по модели и эксперимента. В табл. 2.9 содержатся значения параметров модели (2.77)–(2.90), полученных в результате решения задачи идентификации.
На рис. 2.33, 2.34 показаны временные зависимости важнейших параметров процесса в условиях принудительного термостатирования на уровне 33°С (т. е. без саморегулирования температуры) и с саморегулированием на уровне 41°С. Из графиков видно, что математическая модель отражает основные тенденции процесса в реакторе, наблюдаемые экспериментально.
97
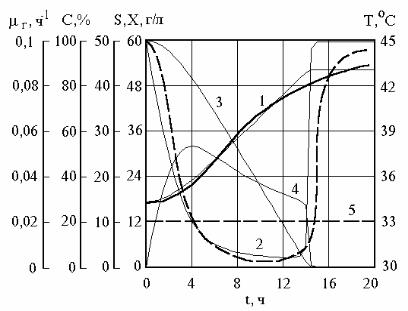
Так, на рис. 2.33 модель демонстрирует адекватное описание не только роста концентрации биомассы, но и весьма своеобразной временной зависимости для концентрации растворенного кислорода. Действительно, во время наиболее интенсивного роста биомассы, эта концентрация должна снижаться из-за интенсивного потребления кислорода из жидкой фазы на эндогенное и экзогенное дыхание.
Рис. 2.33. Проверка адекватности модели для условий работы реактора при T = 33°C. 1 – концентрация биомассы; 2 – концентрация растворенного кислорода в % от насыщения; 3 – концентрация субстрата; 4 – удельная действительная скорость роста микроорганизмов; 5 – температура. Результаты расчета показаны тонкой линией, экспериментальные данные – жирной штриховой и непрерывной линиями
98
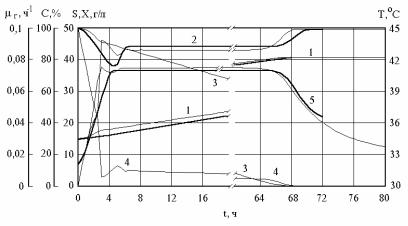
Рис. 2.34 показывает, что в случае с саморегулированием температуры модель также показывает хорошее описание экспериментальных данных. Она адекватно отражает характерные моменты и интервалы времени: момент входа в режим саморегулирования и его длительность, моменты характерного снижения концентрации растворенного кислорода (при t = 5 ч) и его увеличения при выходе из режима саморегулирования. Кроме этого модель удачно отражает уровни всех переменных и тенденции их роста или снижения. Она адекватно отражает основной феномен явления – линейный (отличный от логистической кривой) рост концентрации биомассы.
Максимальные относительные погрешности описания экспериментальных данных рис. 2.33, 2.34 с помощью модели составляют: для концентраций биомассы – 9,4 %; для температуры – 1 %; для растворенного кислорода – до 20 % (в большинстве случаев не превышают 5–6 %).
Рис. 2.34. Проверка адекватности модели для условий работы реактора с саморегулированием температуры. 1 – концентрация биомассы; 2 – концентрация растворенного кислорода в % от насыщения; 3 – концентрация субстрата; 4 – удельная действительная скорость роста микроорганизмов; 5 – температура. Результаты расчета показаны тонкой линией, экспериментальные данные – жирной непрерывной линией
99
