
Аналитическая геометрия / angeom09
.pdf
Лекция 9: Прямая в пространстве
Б.М.Верников
Уральский федеральный университет,
Институт математики и компьютерных наук,
кафедра алгебры и дискретной математики
Лекция 9: Прямая в пространстве












 Вступительные
Вступительные





 замечания
замечания






























































































































































































































Эта лекция посвящена изучению прямой в пространстве. Излагаемый в ней материал можно разбить на семь пунктов:
1 |
Общие и параметрические уравнения кривой в пространстве. |
2 |
Виды уравнений прямой в пространстве. |
3 |
Взаимное расположение прямой и плоскости. |
4 |
Взаимное расположение двух прямых. |
5 |
Расстояние от точки до прямой. |
6Общий перпендикуляр к скрещивающимся прямым. Расстояние между скрещивающимися прямыми.
7 Угол между прямыми. Угол между прямой и плоскостью.
Мы видим, что данная лекция в известной степени аналогична двум предыдущим, но есть и существенные отличия. Например, шестой пункт не имеет аналогов в двух предыдущих лекциях, а в данной лекции нет аналога пунктов о полуплоскостях и полупространствах (это и не удивительно: прямая не делит пространство на две части). Есть и другие отличия. Например, расстояние от точки до прямой в пространстве находится исходя из совсем других соображений, чем расстояние от точки до прямой на плоскости или от точки до плоскости. Отметим еще, что во втором пункте рассматриваются четыре вида уравнений прямой в пространстве (по сравнению с ¾одноименными¿ пунктами из двух предыдущих лекций, здесь отсутствуют аналоги уравнения прямой с угловым коэффициентом и уравнений прямой и плоскости в отрезках). 
Лекция 9: Прямая в пространстве











 Общие
Общие





 уравнения
уравнения





 кривой
кривой





 (определение)
(определение)






























































































































































1◦. Общие и параметрические уравнения кривой в пространстве.
Как и в случаях кривой на плоскости и поверхности, кривую в пространстве можно задавать либо общими, либо параметрическими уравнениями. Общие уравнения в данном случае возникают из следующего простого наблюдения: любую кривую в пространстве можно представить как пересечение двух поверхностей. Поэтому естественным является следующее
Определение
Будем считать, что в пространстве зафиксирована некоторая система координат. Пусть кривая ℓ является пересечением поверхностей σ1 и σ2, поверхность σ1 задана общим уравнением F1(x, y, z) = 0, а поверхность σ2общим уравнением F2(x, y, z) = 0. Тогда уравнения
F1(x, y, z) = 0, |
(1) |
|
F2(x, y, z) = 0 |
||
|
||
называются общими уравнениями кривой ℓ. |
|
Из определения общего уравнения поверхности (см. лекцию 8) вытекает, что точка M с координатами (x0 , y0 , z0 ) лежит на ℓ тогда и только тогда, когда ее координаты удовлетворяют системе уравнений (1).
Лекция 9: Прямая в пространстве











 Общие
Общие





 уравнения
уравнения





 кривой
кривой





 (пример)
(пример)






















































































































































































В качестве примера составим общие уравнения (в прямоугольной декартовой системе координат) окружности радиуса 2 с центром в точке (0, 0, 1), расположенной в плоскости, параллельной плоскости Oxy (см. рис. 1 тремя слайдами ниже). Ясно, что эту окружность можно представить себе как пересечение плоскости, заданной уравнением z = 1, и сферы радиуса 2 с центром в точке (0, 0, 1). Следовательно, наша окружность задается уравнениями
x2 + y2 + (z − 1)2 = 4, z = 1.
Лекция 9: Прямая в пространстве












 Параметрические
Параметрические





 уравнения
уравнения





 кривой
кривой




 (определение)
(определение)










































































































Параметрические уравнения кривой в пространстве определяются вполне аналогично одноименным уравнениям кривой на плоскости (см. лекцию 7).
Определение
Пусть f (t), g(t) и h(t) произвольные функции от одной переменной. Уравнения
x = f (t),
y = g(t), (2)z = h(t)
называются параметрическими уравнениями кривой ℓ, если точка M с
координатами (x0 , y0 , z0 ) лежит на ℓ тогда и только тогда, когда существует число t0 такое, что x0 = f (t0), y0 = g(t0 ) и z0 = h(t0). Переменная t называется параметром.
Лекция 9: Прямая в пространстве












 Параметрические
Параметрические





 уравнения
уравнения





 кривой
кривой




 (пример)
(пример)





























































































































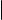

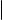
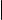





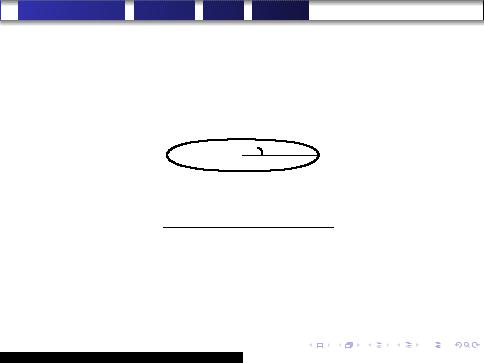
В качестве примера составим параметрические уравнения той же самой окружности, для которой выше мы уже составили общие уравнения. Напомним, что речь идет об окружности радиуса 2 с центром в точке C (0, 0, 1), расположенной в плоскости, параллельной плоскости Oxy (в прямоугольной декартовой системе координат). Пусть M(x, y, z)
произвольная точка на этой окружности. Поскольку плоскость, в которой расположена окружность, параллельна плоскости Oxy, аппликаты точек M и C совпадают, т. е. z = 1. От точки C отложим ненулевой вектор ~a,
сонаправленный с положительным направлением оси Ox, и возьмем в
−−→
качестве параметра t угол между векторами CM и ~a, отсчитываемый против часовой стрелки (см. рис. 1 на следующем слайде). Учитывая, что радиус окружности равен 2, имеем
y = 2 sin t, |
(3) |
x = 2 cos t, |
|
z = 1 .
Нетрудно понять, что и обратно, если координаты (x, y, z) некоторой точки M удовлетворяют этой системе уравнений, то точка M лежит на нашей окружности. Следовательно, (3) параметрические уравнения этой окружности.
Лекция 9: Прямая в пространстве











 Параметрические
Параметрические





 уравнения
уравнения





 кривой
кривой




 (рисунок)
(рисунок)


























































































































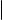





|
|
z |
6 |
|
M |
||
|
|
|
|
|
|||
|
|
|
*r |
|
|
||
|
|
|
|
|
~a - |
|
|
|
C (0, 0, 1) |
r t |
|
|
|||
|
R |
|
= 2 |
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
* |
|
|
|
|
r |
|
y |
||
|
|
|
- |
||||
|
|
|
|
|
|||
|
|
|
O |
|
|
|
x |
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
|
||
Лекция 9: Прямая в пространстве











 Направляющий
Направляющий





 вектор
вектор





 прямой
прямой









































































































































































































2◦. Виды уравнений прямой в пространстве.
Понятие направляющего вектора для прямой в пространстве вводится точно так же, как это было сделано в лекции 7 для прямой на плоскости.
Определение
Любой ненулевой вектор, коллинеарный данной прямой, называется ее
направляющим вектором.
Из этого определения видно, что
 направляющий вектор для данной прямой определен неоднозначно: прямая в пространстве имеет бесконечно много (коллинеарных друг другу) направляющих векторов.
направляющий вектор для данной прямой определен неоднозначно: прямая в пространстве имеет бесконечно много (коллинеарных друг другу) направляющих векторов.
Отметим еще, что
 для прямой в пространстве понятие нормального вектора не определено.
для прямой в пространстве понятие нормального вектора не определено.
Формально можно было бы назвать нормальным вектором прямой в пространстве произвольноый ортогональный ей ненулевой вектор, но никакой пользы для изучения прямой это понятие не дает, поскольку векторов с указанным свойством, так сказать, ¾слишком много¿ они заполняют собой целую плоскость (а именно, плоскость, перпендикулярную к данной прямой).
Лекция 9: Прямая в пространстве












 Параметрические
Параметрические





 уравнения
уравнения





 прямой
прямой











































































































































































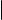

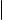



Предположим, что в пространстве зафиксирована система координат с началом в точке O. Пусть ℓ прямая в пространстве, точка M0(x0 , y0 , z0 ) принадлежит прямой ℓ, а вектор ~a = (q, r, s) является ее направляющим вектором. Дословно повторяя рассуждения, проведенные в лекции 7 при выводе параметрических уравнений прямой на плоскости, можно показать, что M ℓ тогда и только тогда, когда выполнены равенства
y = y0 |
+ rt, |
(4) |
x = x0 |
+ qt, |
|
z = z0 |
+ st |
|
|
|
|
для некоторого t. Уравнения (4) называются параметрическими уравнениями прямой в пространстве.
Понятие параметрических уравнений прямой в пространстве согласуется с более общим понятием параметрических уравнений кривой в пространстве, которое было введено выше в данной лекции.
Лекция 9: Прямая в пространстве












 Канонические
Канонические





 уравнения
уравнения





 прямой.
прямой.




 Уравнения
Уравнения





 прямой
прямой




 по
по





 двум
двум




 точкам
точкам












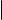

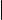
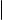





Выражая параметр t из первого, второго и третьего уравнений системы
(4) и приравнивая полученные выражения, мы получаем равенства
x − x0 |
= |
y − y0 |
= |
z − z0 |
, |
(5) |
q |
|
r |
|
s |
|
|
которые называются каноническими уравнениями прямой в пространстве.
Предположим теперь, что мы знаем координаты двух различных точек,
принадлежащих прямой: M0(x0 , y0 , z0) и M1(x1 , y1 , z1 ). Тогда вектор
−−−→
M0 M1 = (x1 − x0 , y1 − y0, z1 − z0 ) коллинеарен прямой и отличен от нулевого вектора, т. е. является направляющим вектором прямой. Подставляя его координаты в канонические уравнения прямой, получаем следующие уравнения, которые называются уравнениями прямой в пространстве по двум точкам:
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
(6) |
x1 − x0 |
|
y1 − y0 |
|
z1 − z0 |
|
|
Лекция 9: Прямая в пространстве
