
- •ИСХОДНЫЕ ДАННЫЕ И СХЕМА МЕХАНИЗМА
- •1. АНАЛИТИЧЕСКИЙ МЕТОД
- •УРАВНЕНИЯ ГЕОМЕТРИЧЕСКИХ СВЯЗЕЙ.
- •ОПРЕДЕЛЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ ЗВЕНЬЕВ МЕХАНИЗМА
- •ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ЗВЕНЬЕВ
- •ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ УЗЛОВЫХ ТОЧЕК
- •2. ГЕОМЕТРИЧЕСКИЕ МЕТОДЫ
- •ОСНОВНЫЕ ТЕОРЕМЫ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- •Определение скоростей точек и угловых скоростей звеньев с помощью мгновенных центров скоростей (МЦС)
- •Определение скоростей точек и угловых скоростей звеньев с помощью теоремы о сложении скоростей
- •Определение ускорений точек и угловых ускорений звеньев с помощью теоремы о сложении ускорений
- •ОСНОВНЫЕ ТЕОРЕМЫ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- •3. АНАЛИЗ РЕЗУЛЬТАТОВ ВЫЧИСЛЕНИЙ
1. АНАЛИТИЧЕСКИЙ МЕТОД
УРАВНЕНИЯ ГЕОМЕТРИЧЕСКИХ СВЯЗЕЙ.
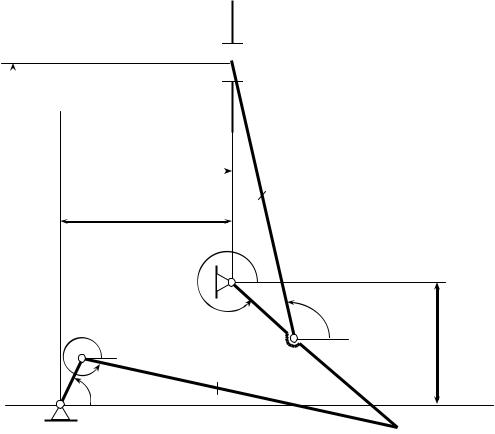
Изобразим плоский механизм в произвольном положении (Рис. 2).
В качестве системы отсчета примем правую декартовую систему координат. Начало системы координат расположим в подшипнике O . Положительные углы поворота в этом случае направлены против часовой стрелки.
 D
D
y
xD
K
a
yD
A ϕ1
O ϕ
O1
ϕ2 ϕ3
C |
b |
|
M
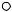 B x
B x
Рис. 2 Расчетная схема механизма
Изобразим углы поворота звеньев ϕk , k =1,2,3 , отсчитывая их от го-
ризонтальной оси Ox в положительном направлении.
Всостав данного многозвенного механизма входят:
•два кривошипаOA и O1B;
•два шатунаAB и CD ;
12
•ползун D ;
•неподвижное звено OO1 .
Кривошипы OA и O1B совершают вращательное движение вокруг неподвижных осей перпендикулярных плоскости xOy и проходящих через точки O и O1 соответственно. Шатуны AB и CD совершают плоскопа-
раллельное движение в плоскости xOy . Ползун D совершает возвратно-
поступательное движение вдоль направляющей параллельной оси Oy .
Для составления уравнений геометрических связей найдем точки механизма, траектории которых известны. К этим точкам относятся шарниры A , B , C и D . Точки A , B и C движутся по окружностям радиусов OA , O1B и O1C соответственно, а ползун D — по прямолинейной траектории параллельной оси Oy (Рис. 2).
Шарнир A принадлежит одновременно шатуну AB и кривошипу OA , для которого известен закон вращательного движения и, следовательно, закон движения точки A определен. Шарнир B принадлежит одновременно шатуну AB и кривошипу O1B, а шарнир C — шатуну CD и
кривошипу O1B. Из двух точек C и B , одновременно принадлежащих кривошипу O1B, одна является зависимой, т.е. определение закона движе-
ния одной точки приводит к возможности определения закона движения для другой.
Так как закон плоскопараллельного движения твердого тела можно определить по двум любым точкам этого тела, в качестве базовых точек, при составлении уравнений геометрических связей, примем точки B и D .
Построим для этих точек векторные контуры, с помощью которых можно составить уравнения геометрических связей (Рис. 3).
13

α |
D |
|
y |
A |
|
|
rA |
ϕ |
|
|
1 |
|
|
ϕ |
O |
|
|
ρO1A |
ϕ |
O1 |
|
|
2 |
rO |
ρO B |
|
1 |
||
|
|
ρ |
|
1 |
|
ρCD |
|
|
|
|
|
|
x |
AB |
|
|
ρO D |
|
|
|
|
|||
|
|
|
|
|
1 |
r |
|
|
|
rD |
|
B |
|
|
|
|
|
a) |
|
|
|
|
|
B |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
O1 |
ϕ3 |
|
|
|
|
|
|
|
|
y |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
O1 |
ρO C |
C |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
O |
|
|
|
б) |
|
||||
|
|
|
|
|
|
|
x |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 3 Векторные контуры для базовых точек механизма |
|
|||||||||||||||
Уравнения геометрических связей в векторной форме будут иметь вид: |
||||||||||||||||
для точки B (Рис. 3 а) |
|
|
|
|
|
|
|
|
|
|
||||||
r |
B = |
r |
A + ρAB = |
rO |
+ ρO B , |
|
(1.1) |
|||||||||
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
||||
для точки D (Рис. 3 б) |
|
|
|
|
|
|
|
|
|
|
||||||
|
r |
D = |
r |
O |
+ ρO C + ρCD . |
|
(1.2) |
|||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|||||||
Преобразуем (1.1) и (1.2) к виду |
|
|
|
|
|
|||||||||||
ρAB − ρO B = |
r |
O − |
r |
A |
= −ρO A , |
|
(1.3) |
|||||||||
1 |
|
|
1 |
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
ρO C + ρCD = |
r |
D − |
rO |
= ρO D . |
|
|
||||||||||
1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
||||
здесь ρO1A — вектор, характеризующий положение шарнира A относи-
тельно центра O1 ; ρO1D — вектор, характеризующий положение шарнира
D относительно центра O1 (Рис. 3).
Проецируя (1.3) на оси декартовой системы координат, получим уравнения геометрических связей в координатной форме (Рис. 2, Рис. 3):
14

xAB |
− xO B |
= xO |
− xA |
= −xO A , |
|
1 |
1 |
|
1 |
yAB |
− yO B |
= yO |
− yA |
= −yO A , |
|
1 |
1 |
|
1 |
xO C + xCD = xD |
− xO |
= xO D , |
||
1 |
|
|
1 |
1 |
yO C + yCD = yD |
− yO |
= yO D |
||
1 |
|
|
1 |
1 |
или в развернутом виде |
|
|
|
|
AB cos(ϕ1 )−O1B cos(ϕ2 )= a −OA cos(ϕ),
AB sin (ϕ1 )−O1B sin (ϕ2 )= b −OA sin (ϕ), (1.4) O1C cos(ϕ2 )+CD cos(ϕ3 )= 0,
O1C sin (ϕ2 )+CD sin (ϕ3 )= yD −b.
В данных уравнениях учтено, что вектор rO1 является постоянным вектором и его проекции на оси декартовой системы координат равны x01 =a , y01 = b ; проекция вектора rD на ось Ox не изменяется с течением времени и равна xD =a .
В уравнениях (1.4) задаваемой функцией является закон вращения ведущего звена ϕ(t), а определяемыми функциями времени являются:
ϕ1 (t), ϕ2 (t), ϕ3 (t), yD (t).
Система (1.4) представляет замкнутую систему уравнений для определения законов движения всех звеньев многозвенного механизма.
Решение уравнений (1.4) можно найти различными методами, как аналитическими, так и численными..
ОПРЕДЕЛЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ ЗВЕНЬЕВ МЕХАНИЗМА
Для нахождения законов движения звеньев механизма запишем первые два уравнения системы (1.4) в следующем виде (Рис. 3 а, Рис. 4)
AB cos(ϕ1 )−O1B cos(ϕ2 )= a −OA cos(ϕ)= −xO A = −O1A cos α, |
||||
AB sin (ϕ )−O B sin (ϕ )= b −OA sin (ϕ)= −y |
1 |
= −O A sin α (1.5) |
||
|
|
|
|
|
1 1 |
|
2 |
O A |
1 |
|
|
|
1 |
|
где xO A =O1A cosα, |
yO A =O1A sin α — проекции вектора ρO A на оси ко- |
|||
1 |
1 |
|
|
1 |
15
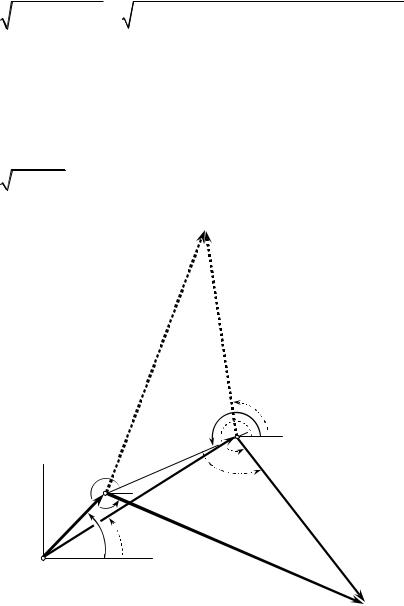
ординат; O1A — модуль этого вектора
O1A = |
xO A |
2 |
+ yO A |
2 |
= |
OO12 + OA2 − 2 OA OO1 cos(ϕ−β); |
|||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
α — угол, характеризующий его направление |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
OA cos(ϕ)−a |
|
|
OA sin (ϕ)− b |
|||
α = arctg |
OA sin (ϕ)− b |
|
, cosα = |
, |
sin α = |
||||||||||||
|
O1A |
O1A |
|||||||||||||||
OA cos(ϕ)−a |
|
|
|
||||||||||||||
здесь OO1 = |
a |
2 |
+ b |
2 |
|
|
|
b |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||||
|
|
, β= arctg — модуль и направление вектора rO1 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
B' 
|
|
|
|
α |
|
ϕ2 ' |
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
O1 |
y |
|
|
|
|
2 |
|
|
|
ϕ1 |
γ2 |
|
||
A |
|
|
||||
|
|
|
||||
O ϕ β
x
 B
B
Рис. 4 Определение угловых координат звеньев
Для нахождения угловой координаты ϕ2 перепишем уравнения (1.5)
в следующем виде
AB cos(ϕ1 )=O1B cos(ϕ2 )−O1A cos α, AB sin (ϕ1 )=O1B sin (ϕ2 )− O1A sin α,
и воспользовавшись известной тригонометрической формулой
cos2 ϕ+ sin2 ϕ=1
16

получим
AB2 = O1B2 + O1A2 − 2 O1B O1A cos(ϕ2 )cos α + sin (ϕ1 )sin α ,
Тогда, учитывая тригонометрическую формулу приведения
cos(ϕ2 )cos α −sin (ϕ1 )sin α = cos(ϕ2 −α),
найдем
cos(ϕ2 − α)= O1B2 + O1A2 − AB2 = cos γ2 2 O1B O1A
Так как cos γ2 является четной функцией углового аргумента, то угол
ϕ2 может иметь два значения
ϕ2 = γ2 + α или ϕ2 = γ2 −α,
что соответствует двум положением четырехзвенника OABO1 относитель-
но O1A при одной и той же угловой координате ведущего звена ϕ (Рис. 4).
Учитывая начальное положение механизма (Рис. 2) принимаем
|
|
O1B |
2 |
+ O1A |
2 |
− AB |
2 |
|
|
ϕ2 |
=α + arccos |
|
|
|
|
(1.6) |
|||
|
2 O1B O1A |
|
|||||||
|
|
|
|
|
|
||||
Для нахождения угловой координаты ϕ1 уравнения (1.5) перепишем в следующем виде
AB cos(ϕ1 )+ O1A cos α = O1B cos(ϕ2 ), AB sin (ϕ1 )+ O1A sin α = O1B sin (ϕ2 )
и используя процедуру, изложенную выше, получим
AB2 + O1A2 + 2 AB O1A cos(ϕ1 )cos α + sin (ϕ1 )sin α = O1B2
или
cos(ϕ1 − α)= O1B2 −O1A2 − AB2 = cos γ1 2 AB O1A
Окончательно, угловая координата ϕ1 равна
17
|
|
O1B |
2 |
− O1A |
2 |
− AB |
2 |
|
|
ϕ1 |
=α + arccos |
|
|
|
|
(1.7) |
|||
|
2 AB O1A |
|
|||||||
|
|
|
|
|
|
||||
Для нахождения остальных неизвестных величин используем оставшиеся два уравнения системы (1.4). Из третьего уравнения (1.4) найдем угловую координату звена CD
ϕ = arccos |
|
−O1C cos(ϕ |
2 |
) |
, |
(1.8) |
3 |
|
CD |
|
|
|
|
|
|
|
|
|
|
|
а из четвертого — вертикальную координату ползуна D |
|
|||||
yD = b +O1C sin (ϕ2 )+CD sin (ϕ3 ) |
(1.9) |
|||||
Уравнения (1.6) — (1.9) позволяют определить угловые координаты звеньев совершающих вращательные и плоскопараллельные движения, а также закон движения звена движущегося поступательно.
18
