Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский государственный архитектурно-строительный университет

Предмет:

B-физика

Файл:

Fizika_Laboratornye_raboty / 44

.pdf

Скачиваний:

Добавлен:

17.03.2016

Размер:

303.58 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

МИНИСТЕРСТВО ОБЩЕГО И

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

КАЗАНСКАЯ ГОСУДАРСТВЕННАЯ АРХИТЕКТУРНО-СТРОИТЕЛЬНАЯ АКАДЕМИЯ

кафедра физики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО ФИЗИКЕ

Лабораторная работа по физике N 44

ИЗУЧЕНИЕ КОЛЕБАНИЙ СВЯЗАННЫХ СИСТЕМ

Казань

1998

КРАТКАЯ ТЕОРИЯ

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

В природе в быту и в технике мы часто наблюдаем периодические процессы: смена дня и ночи, вращение Луны вокруг Земли, колебания маятника часов, движение частей разнообразных машин, переменный электрический ток и т.д. Все такие процессы называются колебаниями. Коле-

баниями называются процессы, характеризуемые той или иной степенью повторяемости во времени. Среди разнообразных колебаний, встречающихся в природе, очень важную роль играют гармонические колебания.

Колебания, при которых какая-либо физическая величина, описывающая некоторый процесс, изменяется со временем по закону косинуса или синуса, называются гармоническими:

x = Acos(ω0t + ϕ).

(1)

Выясним физический смысл постоянных, входящих в это уравнение. Константа А называется амплитудой колебания. Амплитуда — это наибольшее значение, которое может принимать колеблющаяся величина. Выражение ω0t + ϕ, стоящее под знаком косинуса, называют фазой коле-

бания в момент времени t. Постоянная ϕ представляет собой значение фазы в момент времени t = 0 и поэтому называется начальной фазой колебания. Величина ω0 получила название циклической частоты, физический смысл которой связан с понятием периода и частоты колебаний.

Периодом колебаний называют время одного полного колебания. Число колебаний, совершаемых в единицу времени, называется частотой колебаний. Частота ν и период Т связаны соотношением

ν = T1 .

Частота колебаний измеряется в герцах (Гц). 1 Гц — частота периодического процесса, при котором за 1 с происходит одно колебание. Циклическая частота равняется

ω0 = 2πν.

Она показывает сколько колебаний совершается за 2π секунд.

СВОБОДНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Колебания, происходящие в системе, выведенной из состояния равновесия и предоставленной самой себе, называются свободными (или соб-

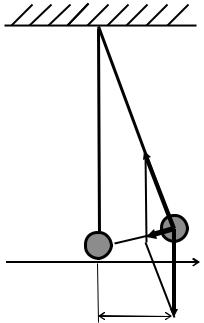
ственными) колебаниями. Рассмотрим, как происходят такие колебания на примере математического маятника. Математическим маятником

называется идеализированная система, состоящая из материальной точки с массой m, подвешенной на невесомой нерастяжимой нити, которая совершает колебания под действием силы тяжести.

Отклоним груз массой m, подвешенный на нить длиной L, от положения равновесия на угол α и отпустим его (рис. 1). Для упрощения задачи предположим, что силы трения малы и ими можно пренебречь. Груз будет двигаться к положению равновесия с ускорением, которое возникло под действием суммы сил: силы тяжести mg , направленной отвесно вниз и си-

лы натяжения нити FrН , направленной вдоль нити к точке подвеса. Возвращающая сила Fr равна векторной сумме сил mgr и FrН , и на-

правлена по касательной в каждой точке траектории движения груза. Ее величина равна

F = mg sinα

Если угол отклонения α мал, то sinα ≈ α, а

F ≈ mgα.

Отклонение груза от положения равновесия обозначим через x. При малых α дугу

αтраектории груза можно считать приближенно прямой. Запишем уравнение движения груза. Согласно второму закону Ньютона те-

FН

x mgr

Рис . 1 всегда противоположны.

ло массой m движется с ускорением			d 2 x
ло массой m движется с ускорением			dt2
под действием равнодействующей			dt2
под действием равнодействующей
силы F	d 2 x
m	d 2 x	= − F
m	dt 2	= − F
	dt 2

В данном случае знак минус перед силой F означает, что направление F и смещения x

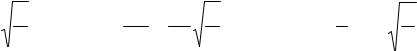
m d 2 x = − mgα. dt2

При малых α можно приближенно считать, что длина дуги траектории гру-

за равна x , т.е. x ≈ Lα. Если заменить α на

, то уравнение можно запи-

сать так

d 2 x

= − mg

или, сокращая на m получаем:

d 2 x

x = 0.

dt 2

Обозначим

= ω02, тогда уравнение примет вид:

d 2 x

x = 0.

(2)

dt 2

+ ω0

Решение этого дифференциального уравнения второго порядка с постоянными коэффициентами таково:

x = Acos(ω0t + ϕ) ,			(3)
в чем легко убедиться, если найти	d 2 x	и подставить в дифференциальное
	dt2

уравнение.

Уравнение (3) аналогично (1). Таким образом мы доказали, что если пренебречь силой трения, при малых отклонениях маятник совершает гармонические колебания с циклической частотой ω0. Частота и период, связанные с ω0, находятся из следующих соотношений:

ω0 =	g	ν=	ω0	=	1	g	T =	1	= 2π	L
	L		2π		2π	L		ν		g

Как видим, период и частота таких колебаний математического маятниказависят только от длины нити и ускорения свободного падения и не зависят от массы груза и от амплитуды колебания (если углы отклонения не превышают 100)

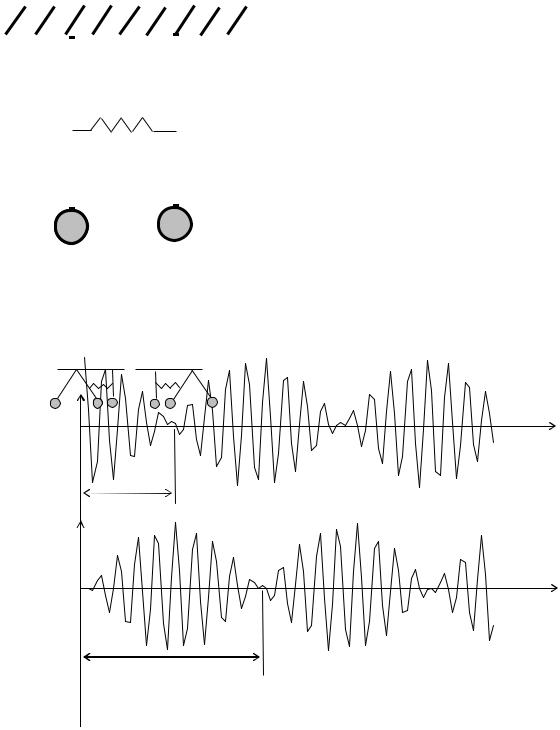
СОБСТВЕННЫЕ КОЛЕБАНИЯ СВЯЗАННОЙ СИСТЕМЫ

Рассмотрим два одинаковых математических маятника, связанных легкой пружинкой, которые способны совершать колебания только в вертикальной плоскости (плоскости листа), проходящей через точки подвеса (рис.2). Колебания одного маятника закономерно связаны с колебаниями другого. Вид этих колебаний зависит от того, как мы приводим систему в движение. СредиНаблюдая колебания за некоторое сравнительно небольшое время, когда еще не сказалось действие сил трения, мы увидим, что колебания каждого из маятников негармоничные.

							Удерживая один из маятников в
							вертикальном положении, второй от-
							клоним от положения равновесия на


							небольшой угол. Затем одновременно
							отпустим оба маятника и запишем на
							один лист колебания обоих маятни-
							ков. x1 и x2 — смещения первого и
							второго маятников от положения рав-
							новесия (рис.3). Вначале первый ма-
							ятник совершает колебания так, как
							если бы второй мы удерживали рукой.
							если бы второй мы удерживали рукой.
							Пружинка между ними заметно сжи-
		Рис.2					мается и разжимается. Сила пружинки
		Рис.2

Tб/2

Тб Рис.3

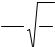
будет действовать на второй маятник, и он постепенно начнет раскачиваться. Так как энергия, сообщенная первому маятнику, будет передаваться отчасти второму, то амплитуда колебаний первого маятника будет постепенно убывать, в то время как амплитуда второго маятника — нарастать. Все это будет продолжаться какое-то время Tб/2, до тех пор, пока первый маятник не остановится, а второй (если потери на трение малы) не будет качаться почти с такой же амплитудой, как и первый в самом начале. Затем маятники меняются ролями: второй раскачивает первый. Процесс полностью повторяется. Маятники будут совершать то нарастающие, то убывающие колебания и через время Tб будут обмениваться энергией. Такие колебания называются биениями, а время Tб — периодом биений. Как бы мы ни выводили маятники из положения равновесия, период биений всегда будет одним и тем же. Колебания каждого из маятников во всех случаях являются негармоническими. Каждый маятник совершает как бы гармоническое колебание, но амплитуда его периодически изменяется с одним и тем же периодом биений Tб.

Из соображений, основанных на симметрии маятников, можно указать два способа возбуждения колебаний, при которых колебания маятни-

ков будут чисто гармоническими:

Первый способ: оба маятника отклонить одинаково в одну сторону и отпустить. Оба маятника будут совершать колебания так, как если бы пружинки не было, она не изменяет своей длины во время колебаний. Если пружинка имеет ничтожный вес, то маятники колеблются с такой же частотой ν, с которой совершал бы свободные колебания один маятник:

νсин=	1	g	(1)
	2π	L

где g — ускорение свободного падения, а L — длина маятника. Такое коле-

бание системы связанных маятников называется синфазным .

Второй способ: оба маятника отклонить одинаково в разные стороны и отпустить. Маятники будут совершать колебания в противофазе, пружинка будет сжиматься и разжиматься, но середина ее останется в покое, и эту точку можно считать закрепленной. Оба маятника находятся в одинаковых условиях и совершают гармонические колебания с периодом Танти . Период антифазных колебаний Танти будет меньше периода синфазных колебаний Тсин, так как во втором случае к возвращающей силе маятника присоединяется еще и возвращающая сила пружинки. Так как движения маятников абсолютно симметричны, составим уравнение движения для одного из связанных маятников (рис.4).

F упр

На маятник , rкроме

возвращающей силы F , действует еще и сила упругостиr

растянутой пружины F упр = − ka, где k — жесткость пружины, а a — удлинениеr пружи-

ны. Силы F и F упр имеют разные точки приложения,

поэтому составим уравнение движения для моментов этих сил, т.е.

Mупр = Fупрd = – kad и M = – FL= – mgαL

	x	где d — расстояние от точки
		подвеса маятника	до точки
Рис.4	mg
		крепления упругой	связи к

стержню маятника, m — масса груза, а L — длина маятника. В соответствии с урав-

нением динамики вращательного движения равнодействующий момент сил, приводящий в движение маятник, можно записать так:

m d 2 x L = – kad − mgαL. dt

Если угол отклонения маятника от положения равновесия невелик, то под-

ставив значение α =

и a =

x , и поделив уравнение на mL, получим:

d 2 x

x +

k d 2

x = 0

m L2

Решение этого дифференциального уравнения второго порядка с постоянными коэффициентами записывается следующим образом:

x=A sin(	g	+	k d 2	t+α),
	L		m L2

где	g	+	k d 2	= ω0 циклическая частота антифазных гармонических
где	L	+	m L2	= ω0 циклическая частота антифазных гармонических
	L		m L2
колебаний маятников, связанных легкой пружинкой. Итак
				νанти=	1	g	+	k d 2	.	(2)
				νанти=	2π	L	+	m L2	.	(2)
					2π	L		m L2

Если система двух маятников совершает колебания с νанти или νсин , колебания будут гармоническими, во всех других случаях в системе воз-

никнут биения с частотой

νб = νанти – νсин .

(3)

Причем эта частота не зависит от способа возбуждения колебаний и от начальных отклонений маятников.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ БИЕНИЙ

Чтобы получить математическое объяснение биений мы должны сложить два гармонических колебания близкой частоты. Сложим два гармонических колебания различной частоты (для двух одинаковых маятни-

ков эти частоты равны νанти и νсин ). Предположим, что амплитуды этих колебаний равны, а начальные фазы равны нулю.

x1 = A cos (2πν1t) x2 = A cos (2πν2t).

Суммарное колебание рассчитывается так

x= x1 + x2 = A[cos(2πν1t) + cos (2πν2t)] =

2A cos π(ν2 – ν1) t cos 2π	ν1 + ν2	t
	2

Если частоты близки, то можно считать, что	ν1 + ν2	≈ ν , а ν2 – ν1 = νб
	2

Получаем, что

x = (2A cos πνб t) cos 2πνt.

Можно считать результирующее колебание гармоническим колеба-

нием с частотой ν = ν1 + ν2 , амплитуда которого периодически изменяет-

ся со временем с частотой νб = ν2 – ν1, или, как говорят, пульсирует.

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СВЯЗАННЫХ СИСТЕМ

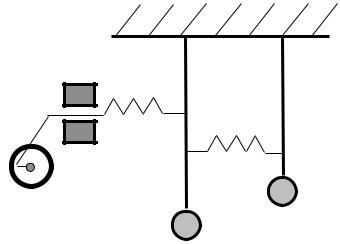
В отличие от свободных, вынужденные колебания происходят под
действием внешней периодической силы. Вынужденные колебания проис-
ходят всегда с той же частотой, с которой изменяется внешняя сила. Ам-
плитуда вынужденных колебаний зависит не только от величины дейст-
вующей силы, но и от ее частоты. Амплитуда вынужденных колебаний
резко возрастает, если частота силы близка к частоте собственных колеба-
ний системы.
Явление резкого возрастания амплитуды колебаний , когда частота
внешней силы приближается к собственной частоте системы, называет-
		ся резонансом. Под действи-
		ем внешней гармонической
		силы F частоты Ω (рис.5),
		приложенной			к	одному		из
		связанных		маятников,			оба
		маятника		будут		совершать
		гармонические				вынужден-
		ные колебания с частотой Ω.
		Амплитуды колебаний каж-
		дого из маятников будут за-
		висеть от частоты Ω. Резо-
Ω		нанс колебаний, или коле-
		бания	обоих		маятников			с

	Рис.5	максимальной			амплитудой,
		будет наблюдаться тогда, ко-

		гда одна из собственных час-
тот связанных маятников равна частоте внешней силы.				Зависимость ам-
плитуды колебаний	А одного из маятников от частоты при постоянной
амплитуде внешней силы показана на рис. 6, где видны два резонансных
пика вблизи собственных частот маятников ω1 и ω2 .В случае разной длины
маятников резонанс колебаний будет наблюдаться, когда ω1 и ω2 — собст-
венные частоты колебаний первого и второго маятников. При первом ре-
зонансе будут наблюдаться синфазные колебания маятников, но угол от-
клонения длинного маятника будет больше, так как частота ω1 близка к
собственной частоте длинного маятника. При втором резонансе колебания
маятников будут антифазными с частотой ω2 , близкой к собственной час-
тоте короткого маятника.

				Картина
А			“двугорбого” ре-
А			зонанса наблюда-
			зонанса наблюда-
			ется и при равен-
			стве	параметров
			маятников.		В
			этом	случае	час-
			тотами ω1		и ω2
			будут	частоты,
ω1	ω2	Ω	соответствующие
ω1	ω2	Ω	синфазным и ан-
		Рис.6	синфазным и ан-
			тифазным собст-

венным колебаниям связанных маятников.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1.Включить в сеть шнур питания миллисекундомера. Нажать на кнопку СЕТЬ, расположенную на лицевой панели миллисекундомера, при этом должны загореться лампочки цифровой индикации. Качнуть оба маятника. При пересечении прерывателем, закрепленным на стержне одного из маятников, светового потока фотодатчика, начнется отсчет периодов и времени колебаний. При нажатии кнопки СТОП убедиться в том, что отсчет периодов и времени прекращается в момент окончания очередного периода колебаний.

2.Нажать на кнопку СБРОС. При этом на лампочках цифровой индикации должны загореться цифры “0”.

3.Отсоединить маятники от связи со стержнем возбудителя колебаний. Для этого осторожно вытащить верхнюю пару пружинок и зацепить их за верхнюю рамку.

4.Определить частоту собственных синфазных колебаний маятников, из-

мерив Тсин. Для этого надо оба маятника отклонить на одинаковый угол (5 — 6о) в одну сторону и одновременно отпустить. Период следует определять по времени 10 полных колебаний маятников. Сделайте 5 изме-

рений Тсин и определите среднее значение Тсин . Занесите данные в таблицу.

5.Определить частоту собственных антифазных колебаний, измерив Танти. Для этого надо оба маятника отклонить в разные стороны на одинаковый угол (5 — 6о) и одновременно отпустить. Период следует опреде-

лить по времени 10 полных колебаний. Сделайте 5 измерений Танти и определите среднее значение Тантиф. Занесите данные в таблицу.

1 / 21 2 > Следующая >>>

Соседние файлы в папке Fizika_Laboratornye_raboty

#
17.03.2016116.88 Кб1338.pdf
#
17.03.2016407.79 Кб1439.pdf
#
17.03.2016120.65 Кб144.pdf
#
17.03.2016326.46 Кб1540.pdf
#
17.03.2016235.31 Кб1441.pdf
#
17.03.2016303.58 Кб1344.pdf
#
17.03.2016153.03 Кб1345.pdf
#
17.03.2016229.41 Кб1346.pdf
#
17.03.2016190.19 Кб1447.pdf
#
17.03.2016598.33 Кб1348.pdf
#
17.03.2016167.99 Кб1351.pdf