Дифференциальное исчисление
Лекция 1
Автор: И. В. Дайняк, к.т.н., доцент кафедры высшей математики БГУИР
ПРОИЗВОДНАЯ ФУНКЦИИ В ТОЧКЕ
Дифференциальное исчисление |
Автор: И. В. Дайняк, к.т.н., доцент |
кафедры высшей математики БГУИР |
Производная функции в точке
Пусть функция f (x) определена в некоторой окрестности точки х0.
Определение 1:
Производной функции f (x) в точке x0 называется число, обозначаемое f ’(x0), равное пределу отношения
|
f (x) f (x0 ) |
|
при |
x x0 |
|
|
x x0 |
||||
|
|
|
|
||
если этот предел существует. |
|
|
|
||
|
f (x0 ) lim |
f (x) f (x0 ) |
|
||
|
x |
x0 |
|||
|
x x0 |
||||
Дифференциальное исчисление |
Автор: И. В. Дайняк, к.т.н., доцент |
кафедры высшей математики БГУИР |
Производная функции в точке
Определение 2:
Производная функции f (x) в точке x0 есть предел отношения
её приращения |
f (x0 ) |
к соответствующему приращению |
|||
её аргумента |
x при |
x 0 |
|
|
|
|
|
f (x0 |
x) f (x0 ) |
lim |
f (x0 ) |
|
|
|
|||
f (x0 ) lim |
|
x |
x |
||
x 0 |
|
x 0 |
|||
Обозначения:
Производную функции y = f (x) принято обозначать так:
y (x ); |
y |
(x ); |
f (x ); df (x0 ) |
; |
dy(x0 ) . |
||
0 |
x |
0 |
x |
0 |
dx |
|
dx |
|
|
|
|
|
|
||
Дифференциальное исчисление |
Автор: И. В. Дайняк, к.т.н., доцент |
кафедры высшей математики БГУИР |
Односторонние производные функции в точке
Правая производная:
Если функция f (x) определена в некоторой правой полуокрестности точки x0 , то её правой производной называется предел
f (x |
0) f (x |
) lim |
f (x) f (x0 ) |
lim |
f (x0 ) |
|
|
||||||
0 |
|
0 |
x x0 0 |
x x0 |
x 0 |
x |
|
|
|
||||
Левая производная:
Если функция f (x) определена в некоторой левой полуокрестности точки x0 , то её левой производной называется предел
f (x |
0) f (x |
) lim |
f (x) f (x0 ) |
lim |
f (x0 ) |
|
|
||||||
0 |
|
0 |
x x0 0 |
x x0 |
x 0 |
x |
|
|
|
||||
Дифференциальное исчисление |
Автор: И. В. Дайняк, к.т.н., доцент |
кафедры высшей математики БГУИР |
Производная функции в точке
Пример 1:
Найти производную функции |
exsin 5x 1, |
x 0 |
|
f (x) |
0, |
x 0 |
|
|
|
||
в точке х0 = 0.
Пример 2:
Найти производную функции f (x) | x 1| в точках х1 = 0 и х2 = 1.
Дифференциальное исчисление |
Автор: И. В. Дайняк, к.т.н., доцент |
кафедры высшей математики БГУИР |
Производная функции в точке
Теорема:
Если функция f (x) имеет производную в точке x0, то она непрерывна в точке x0.
Обратное утверждение неверно.
Дифференциальное исчисление |
Автор: И. В. Дайняк, к.т.н., доцент |
||
кафедры высшей математики БГУИР |
|||
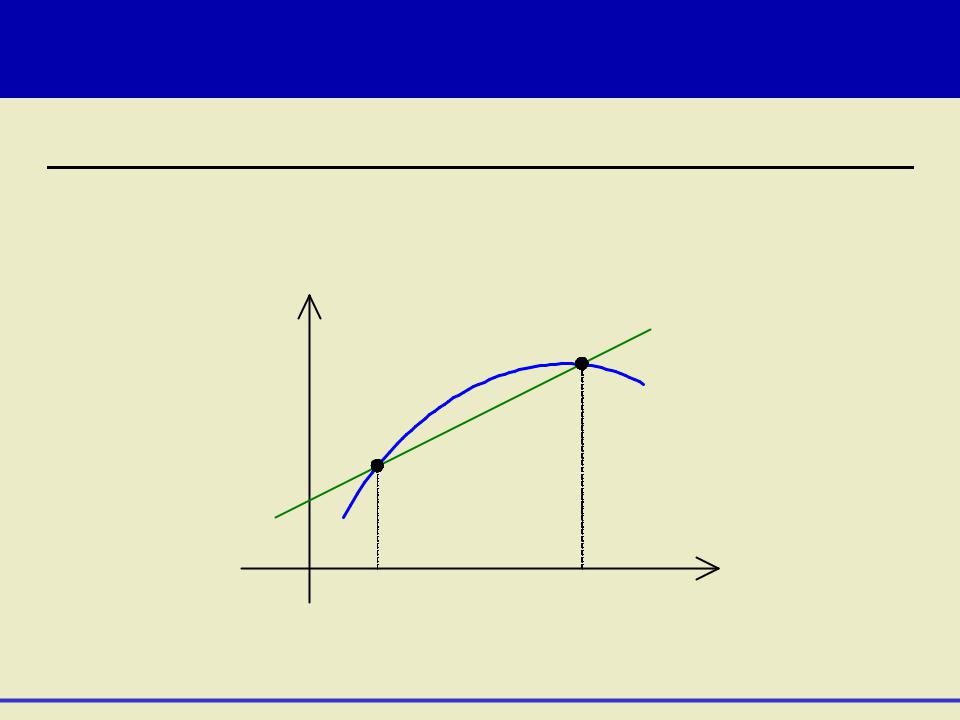
Геометрический смысл производной функции в точке |
|||
Пусть f (x) – непрерывная функция, определённая в |
|||
некоторой окрестности точки x0. |
|
|
|
Рассмотрим две точки: |
A(x0 , f (x0 )) |
B(x1, f (x1)) |
|
Y |
|
B |
|
|
f (x) |
|
|
|
|
|
|
A |
|
|
|
|
|
|
X |
x0 |
|
x1 |
|
Дифференциальное исчисление |
Автор: И. В. Дайняк, к.т.н., доцент |
|
кафедры высшей математики БГУИР |
||
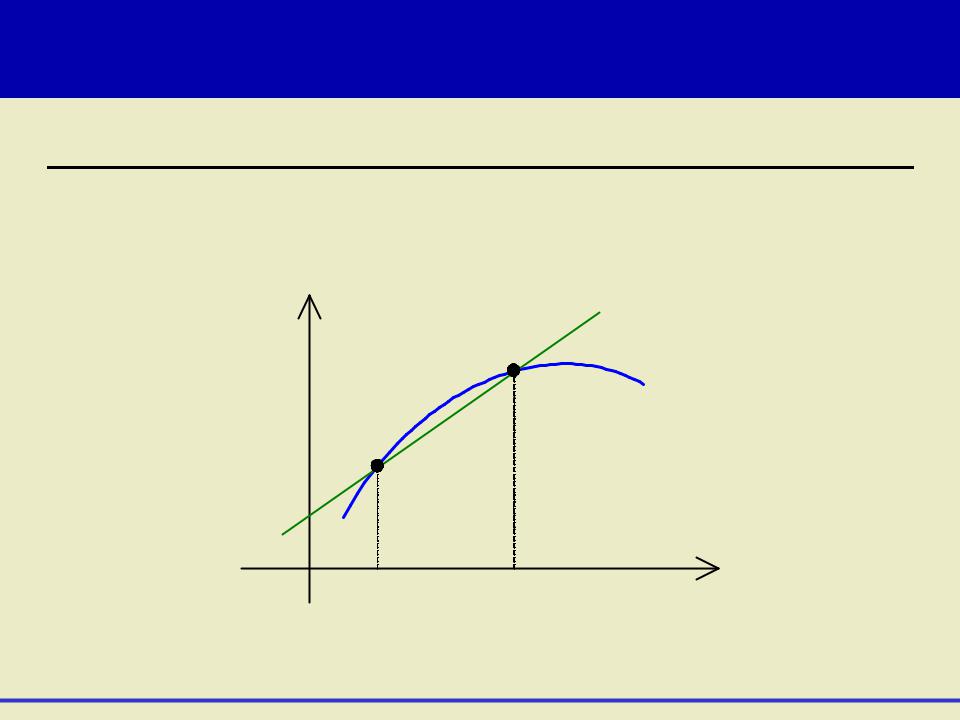
Геометрический смысл производной функции в точке |
||
Приблизим точку В к точке А: |
|
|
Y |
B |
|
f (x) |
||
|
||
A |
|
|
|
X |
|
x0 |
x1 |
|
Дифференциальное исчисление |
Автор: И. В. Дайняк, к.т.н., доцент |
|
кафедры высшей математики БГУИР |
||
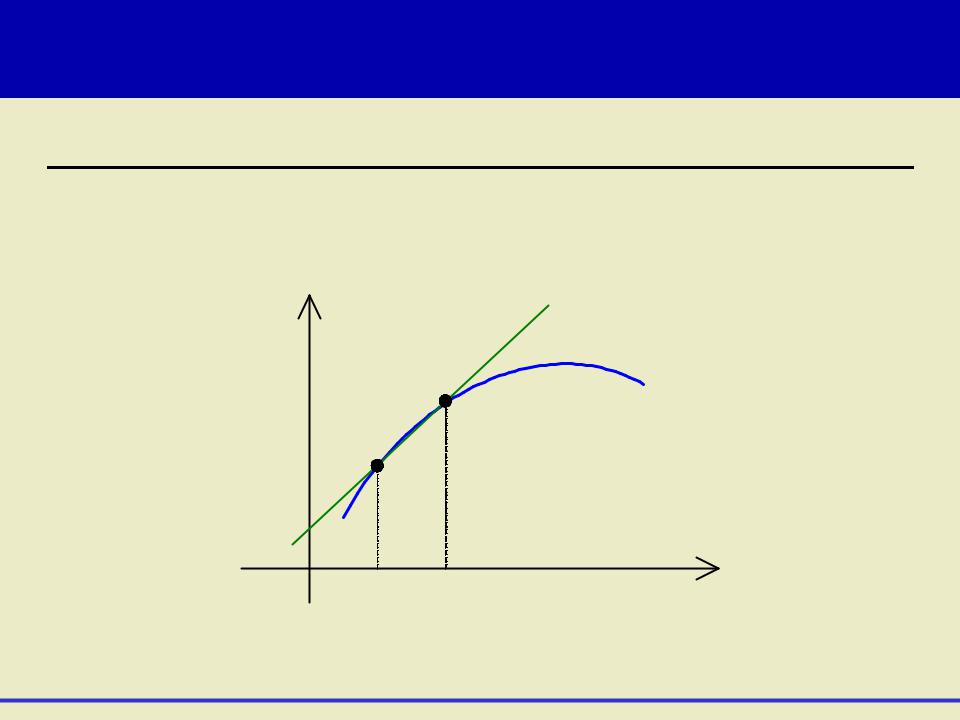
Геометрический смысл производной функции в точке |
||
Приблизим точку В к точке А: |
|
|
Y |
B |
|
|
|
|
|
f (x) |
|
A |
|
|
|
|
X |
x0 |
x1 |
|
Дифференциальное исчисление |
Автор: И. В. Дайняк, к.т.н., доцент |
|
кафедры высшей математики БГУИР |
||
Геометрический смысл производной функции в точке |
||
Приблизим точку В к точке А: |
|
|
Y |
|
f (x) |
|
B |
|
|
|
|
A |
|
|
|
|
X |
x0 |
x1 |
|