Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

VbIshka / Специальные главы математики

.pdf

Скачиваний:

Добавлен:

16.03.2016

Размер:

1.16 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

Министерство образования и науки Российской федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

™Кузбасский государственный технический университет имени Т.Ф. Горбачева¡

Г. А. Казунина

СПЕЦИАЛЬНЫЕ ГЛАВЫ МАТЕМАТИКИ

Учебное пособие

Рекомендовано учебно-методической комиссией направления 140400.62 ™Электроэнергетика и электротехника¡

в качестве электронного учебного пособия

Кемерово 2012

Рецензенты:

Жирнова Т.С. – доцент кафедры математики

Каширских В.Г. – председатель учебно-методической комиссии направления подготовки 140400.62 ™Электроэнергетика и электротехника¡

Казунина Галина Алексеевна. Специальные главы математики: учебное пособие для самостоятельной студентов направления подготовки 140400.62 ™Электроэнергетика и электротехника¡, профиль ™Электропривод и автоматика¡ [Электронный ресурс] / Г.А. Казунина. – Электрон. дан. - Кемерово: КузГТУ, 2012. – 1 электрон. опт. диск (CD-ROM); 12 см. – Систем. требования: любой компьютер, поддерживающий Microsoft Windows-7 и выше, мышь. - Загл. с экрана.

Приводятся элементы теории, примеры решения задач и содержание самостоятельной работы студентов по темам курса ™Специальные главы математики¡, который согласно рабочей программе изучается в 3 семестре. Пособие предназначено для организации самостоятельной работы студентов

КузГТУКазунина Г. А.

Пособие предназначено для организации самостоятельной работы студентов направления подготовки 140400.62 ™Электроэнергетика и электротехника¡, профиль ™Электропривод и автоматика¡ по дисциплине ™Специальные главы математики¡ согласно соответствующей рабочей программе. Форма самостоятельной работы – расчетно-графические работы (РГР). Каждая расчетнографическая работа предваряется изложением теоретического материала в объеме, необходимом для выполнения работы, и подробным рассмотрением задач по каждой теме.

РГР 1 (0,139 ЗЕ)

Передаточная функция. Импульсная и переходная характеристики. Различные формы записи решений линейных дифференциальных уравнений

Литература

1.Казунина Г.А. и др. Дискретные и интегральные преобразования: КузГТУ.

– 1999

2.Казунина Г.А. Преобразования Фурье. Преобразования Лапласа: учеб. пособие [электронный ресурс].- КузГТУ.- 2009

Содержание работы.

Для динамических систем, заданных дифференциальными уравнениями, найти следующие характеристики:

1. Передаточную функцию H ( p) Y ( p) - отношение изображения по Лапла-

X ( p)

су выходного сигнала к изображению входного сигнала при нулевых начальных условиях

2. Импульсную переходную характеристику систем

(реакцию системы на импульсное входное воздействие) w(t) H ( p)

3.Переходную характеристику системы (реакцию системы на ступенчатое воз-

действие) h(t) w( )d

4.Найти реакцию системы на входное воздействие двумя способами а) опера-

торным методом, б) методом свертки

А) x(t) eat (t)

0,	t 0
	0 t	T
В) x(t) E,	0 t	T
	t T
0,	t T

5. Найти частотную передаточную функцию

S ( ) H (i ) A( )ei ( ) U ( ) iV ( ) , а также

А) амплитудно – частотную характеристику

A( ) H (i ) 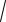U 2 V 2 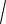H (i )H ( i )

В) фазово-частотную характеристику

V ( )

( ) аrctg .

U ( )

С) Постройте графики функций

( , A( )), ( , ( )), (U ( ), V ( )) . Примечание: последний график можно построить как функцию параметра ω, используя компьютер.

Пример выполнения задания (вариант 10).

1.Из уравнения Ty (t) y(t) kx (t) , переходя к изображениям Лапласа при нулевых начальных условиях, находим передаточную функцию:

TpY ( p) Y ( p) k p X ( p)

Y ( p)(Tp 1) k p X ( p)
H ( p)	Y ( p)	kp	kp
H ( p)				1	.
	X ( p)	Tp 1	T ( p	1	.
					)
					)

2.Поскольку передаточная функция не является правильной дробью, то для перехода к оригиналу выделяем целую часть и остаток

H ( p)

)

(t)

e T (t) w(t)

T 2

T p

3. В результате импульсная переходная характеристика имеет вид

		5
	k		k		t

w(t)		(t)		e T (t) .
w(t)	T	(t)	2	e T (t) .
	T		T

Здесь обязательно надо повторить по указанным выше учебным пособиям свойства импульсной функции Дирака и ступенчатой функции Хевисайда. Переходную характеристику находим как интеграл от импульсной переходной характеристики:

h(t) w( )d

( )d (

e T d ) (t)

(t)

T 1) (t)

(1 e T 1) (t)

e T (t)

4. Реакцию системы на внешнее воздействие находим двумя способами. Так для сигнала x(t) eat получаем:

Способ 1.

Y ( p ) H ( p ) X ( p )

pe pt

(

)

T p

p a

T p a

p a

kae at

ke T

(t )

T (1 Ta )

1 aT

Способ 2 Используем формулу свертки с импульсной переходной или переходной характеристикой, например, формулу Дюамеля:

aea e

T d (t)

(t)

y(t) x(0)h(t) x

( )h (t )d e

aT 1

T t

a k e

kae

(t)

1 at

T (1 Ta)

0,	t 0
	0 t	T получаем:
Для входного сигнала x(t) E,	0 t	T получаем:
	t T
0,	t T

Способ 1.

Y ( p ) H ( p ) X ( p )

t T

e T (t ) e

T (t T )

Способ 2.

y(t) h (t)x(0) (t)

( )h(t )d (t) x(T )h (t T ) (t T )

t T

0 e

(t)

d (t)

(t T )

(t) e

(t T )

5. Находим частотную переходную характеристику

H (i )

k i

k i (1 T i)

kT 2

k i

;

1 T i

1 T 2 2

U( ) Re H (i )

kT 2

V ( ) Im H (i )

;

1 T

2 2

1 T

2 2

А) Амплитудно-частотная характеристика

k i

A( )

H (i ) H ( i )

1 i T 1 i T

1 T 2 2

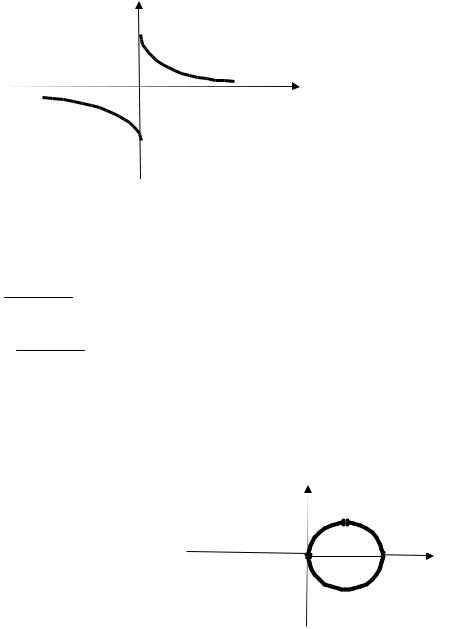
A(ω)

Б) Фазово-частотная характеристика

( ) arctg	V ( )	arctg		1
( ) arctg		arctg		T
U ( )				T

			( )

С) Амплитудно-фазовая характеристика строится как кривая в координатах (U ,V ) . Кривую можно построить аналитически, исключив параметр ω из системы уравнений:

kT 2 U 1 T 2 2 ;

V 1 T 2 2 ;

2 2

2 U 2

2 2

k V (T 1)

U V

2 2

T V

Окончательно получаем смещенную окружность

	k 2	V 2	k
U
			4T	2
	2T

ВАРИАНТЫ

1) Ty y kx(t) ,

2) y 2 y 2 y kx(t)

3) y 5 y 6 y kx(t)

5) y 2 y y kx(t)

7) Ty y kx(t)

9) y kx (t)

4)y a2 y kx(t)

6)y kx(t)

8)y kx(t) k1 x (t) 10) Ty y kx (t)

РГР 2 (0,139 ЗЕ)

Решение разностных уравнений и систем уравнений методом Z-преобразований

Литература

1.Казунина Г.А. и др. Дискретные и интегральные преобразования/ КузГТУ.

– Кемерово, 1999.

2.Казунина Г.А. Преобразования Фурье. Преобразования Лапласа: учеб. пособие [электронный ресурс] / КузГТУ. – Кемерово, 2009.

Содержание работы

Методом Z-преобразований найти решение указанных разностных уравнений и систем уравнений

Теоретическое введение

Z -преобразованием для числовой (действительной или комплексной) бесконечной последовательности an x n называют функцию комплексной пере-


менной X (z), которая определяется как разложение в ряд Лорана в окрестности
бесконечно удаленной точки z :
		x n
X ( z )		z	n .
	n 0	z

Если функция x n является решетчатой функцией и удовлетворяет усло-

вию

, то ряд Лорана сходится в области

то есть вне

x n

круга с центром в начале координат и радиусом R e

. Функция

X (z) яв-

ляется в этой области аналитической функцией.

, n

0 .

Пример 1. Найти Z-преобразование функции x n

Разложение функции в ряд Лорана имеет вид:

		n			n
X (z) A				A		.
		z	n
	n 0			n 0	z

Так как данный ряд является геометрической прогрессией со знаменателем

q		и первым членом прогрессии, равным			A, то сумма ряда равна:
	z
			A			Az
		X (z)					.
			1			z
				z

Область сходимости ряда: z .

В дальнейшем будем обозначать соответствие между решетчатой функцией и ее Z-преобразованием следующим образом:

		n		Az
			z .
X n	X (z); A

Пример 2. Найти Z-преобразование для функции x n 1.

Разложение функции в ряд Лорана имеет вид:

		1		1		z
X (z)							.
X (z)		z	n		1		.
	n 0	z		1	1	z 1
				1

Область сходимости ряда определяется соотношением:	1		1 или	z	1.

		z

Полную таблицу преобразований найдете в указанной выше литературе.

Восстановить решетчатую функцию-оригинал (общий член последовательности) можно используя общую формулу для коэффициентов ряда Лорана в окрестностях z :

N	n 1	.
ˆ	n 1
x n res X	( z k ) z k
k 1

Сумма вычетов берется по всем особым точкам, лежащим в конечной части плоскости.

Пример. Восстановить решетчатую функцию

	1
X (z)	.
	(z 2)(z 3)

Функцию x[n] восстановим по формуле для коэффициентов ряда Лорана:

	n		.
		n 1
x n	res X(zk )zk

k 1

Сучетом того, что данная функция

=2 и z = 3, получаем:

X(z) имеет простые полюсы в точках z

	z n 1			z n 1
x n r e s			r e s

	( z 3)( z 2 )	z 2		( z 3)( z 2 )	z 3

z n 1

n 1

z 3

z 2

z 3

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в папке VbIshka

#
16.03.2016362.13 Кб10Задания Математика 1 семестр ЭА.pdf
#
16.03.20162.69 Mб26Математика 2 Семестр.pdf
#
16.03.2016430.9 Кб8Метод.Указания для практических занятий.pdf
#
16.03.20161.13 Mб12Метод.Указания для самостоятельной работы студентов.pdf
#
16.03.2016474.13 Кб14Специальные главы математики 2.pdf
#
16.03.20161.16 Mб62Специальные главы математики.pdf
#
16.03.20169.19 Mб31Специальные главы математики.ppt