2.3. Решение однородных систем линейных уравнений. Фундаментальная система решений

Рассмотрим однородную систему уравнений, в которой все свободные члены в правой части уравнений равны нулю:

(2.19)

или в матричной форме:

Здесь основная матрица системы, где

Пусть – ранг матрицыА. Если , то имеющееся у системы нулевое решение– единственное.

Рассмотрим теперь случай, когда <n.

Прямой ход метода Гаусса приводит к системе:

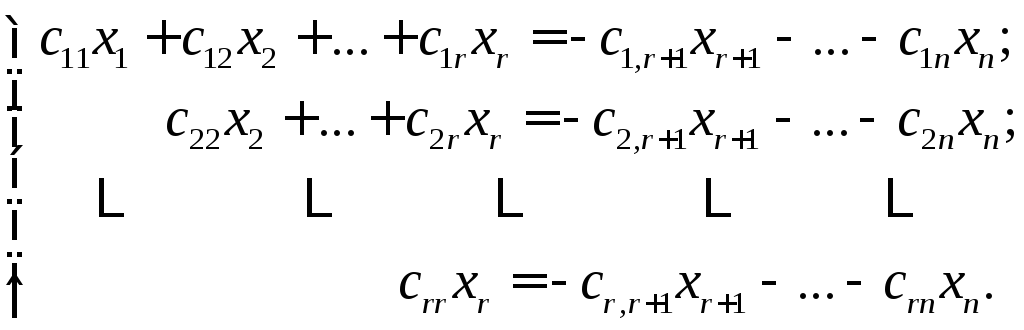(2.20)

Рассмотрим далее несколько иной подход для решения системы (2.20) в отличие от того, как решалась система (2.17) (сравните с решением примера 10). Полученные результаты будут использованы в дальнейшем.

Фундаментальная система решений ЛСУ состоит из матриц-столбцов (векторов) размерности :

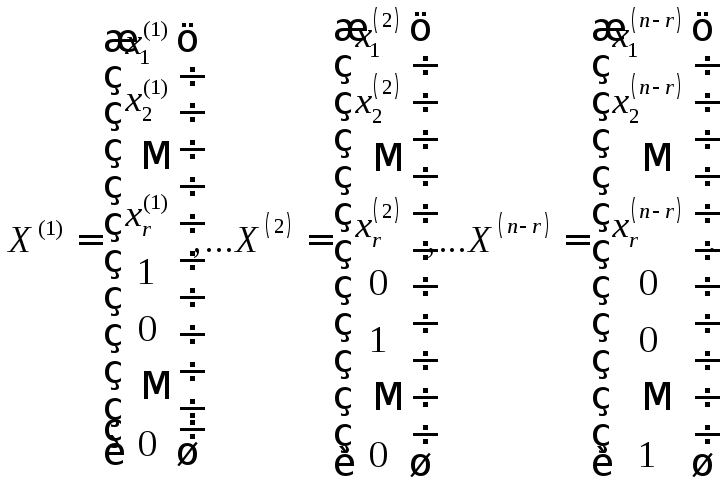(2.21)

В первом векторе неизвестныеполучены на обратном ходе метода Гаусса, если свободным переменным системы (2.20) придавать значения:

(2.22)

Чтобы получить второй вектор-столбец , подставим в систему (2.20) значенияи решим полученную систему на обратном ходе метода Гаусса. Продолжая так и далее и выполнившагов, получаем фундаментальную систему решений (2.21), после чего можно записатьобщее решение системы (2.19) в виде:

,(2.23)

где – произвольные числа.

Формула (2.23) означает, что любое (из бесчисленного множества) решение Х исходной системы (2.19) может быть получено, если соответствующим образом подобрать в ней константы

Пример 11. Решить однородную систему уравнений:

(2.24)

Решение.

Прямой ход (расширенную матрицу в случае однородной системы не записываем):

~~.

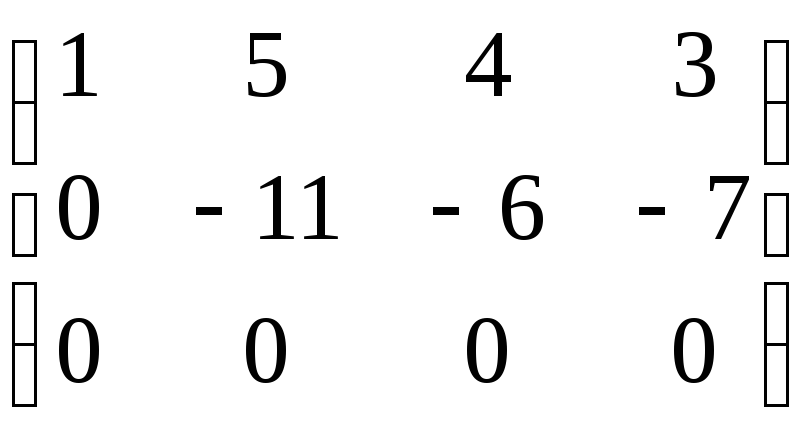Ранг основной (и расширенной) матрицы системы ;

−число свободных неизвестных, в качестве которых выбираем иВ результате получаем систему:

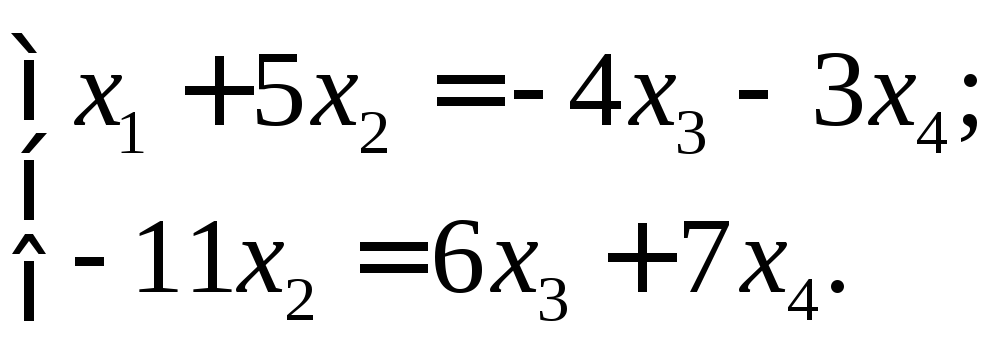(2.25)

Обратный ход.

Положим и, подставляя эти значения в систему (2.25), получим:,следовательно, первый вектор-столбец, входящий в фундаментальную систему решений, имеет вид:

Полагая в системе (2.25), получаем второй вектор-столбец, входящий в фундаментальную систему решений:

Общее решение системы (2.24) имеет вид:

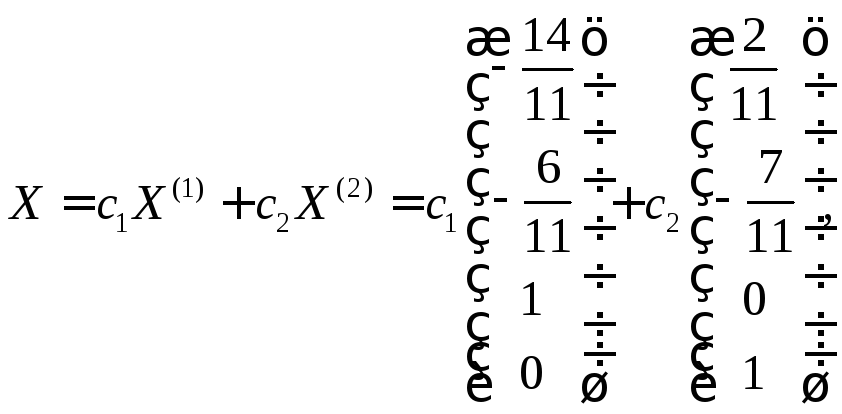где − произвольные числа.

Если положить , то искомое общее решениеможно записать в более компактном виде вектор-столбца: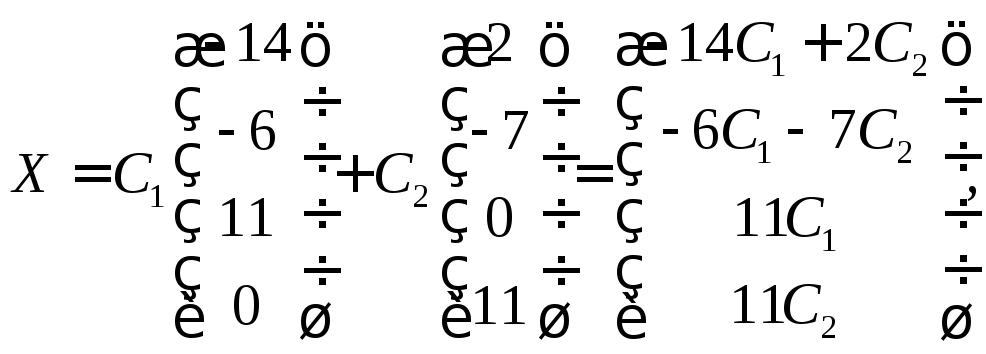где – произвольные числа.

Расписывая предыдущее матричное равенство покомпонентно, получаем решение примера 11 в виде:

где − произвольные числа.

Библиографический список

1. Виленкин И. В. Высшая математика для студентов экономических, технических, естественнонаучных специальностей вузов / И. В. Виленкин, В. М. Гробер. Ростов-на-Дону: Феникс, 2004.

2. Выгодский М. Я. Справочник по высшей математике / М. Я. Выгодский М.: Астрель; АСТ, 2005.

3. И л ь и н В. А. Линейная алгебра: Учебник / В. А. Ильин. М.: Физмат­лит, 2004.

4. Кремер Н. Ш. Математика для экономистов: от арифметики до эко­нометрики / Н. Ш. Кремер, Б. А Путко, И. М. Тришин. Учебно-спра-вочное пособие. М.: Высшее образование, 2007.

5. Кремер Н. Ш. Высшая математика для экономических специальнос-тей / Н. Ш. Кремер, М. Н Фридман. М.: Высшее образование, 2008. Ч. 1, 2.

Учебное издание

ФИЛИМОНОВА Тамара Алексеевна,

ЦАРЕГОРОДЦЕВ Евгений Алексеевич,

ШВЕД Елена Анатольевна

ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ