
- •Т. А. Филимонова, е. А. Царегородцев, е. А. Швед
- •1. Матрицы и определители
- •1.1. Матрицы. Типы матриц
- •1.2. Определители, способы их вычисления
- •1.3. Операции над матрицами
- •1.4. Обратная матрица и ее вычисление
- •1.5. Ранг матрицы
- •2. Системы линейных алгебраических уравнений
- •2.1. Матричная запись системы линейных уравнений.
- •2.2. Методы решения систем линейных уравнений
- •2.3. Решение однородных систем линейных уравнений. Фундаментальная система решений
- •Часть 1
- •644046, Г. Омск, пр. Маркса, 35
2.1. Матричная запись системы линейных уравнений.
Теорема Кронекера – Капелли
Линейной системой
m уравнений с n неизвестными
![]() (ЛСУ) называется
система вида
(ЛСУ) называется
система вида
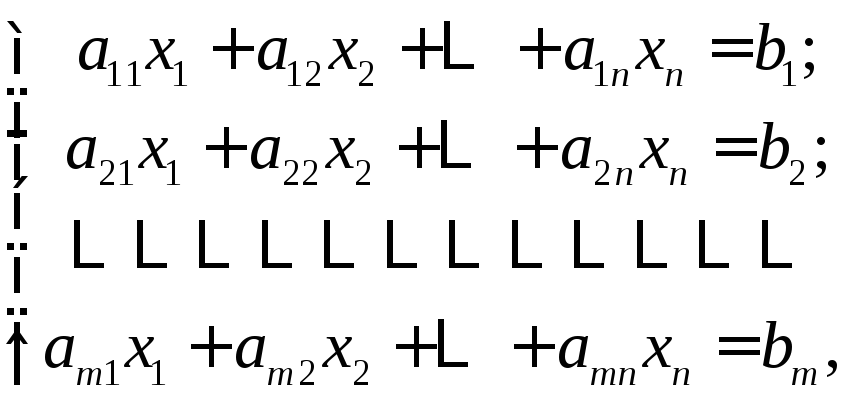 (2.7)
(2.7)
где
![]() –
коэффициент (число) при неизвестном
–
коэффициент (число) при неизвестном![]() вi-м
уравнении;
вi-м
уравнении;
![]() – свободный член в этом уравнении,
– свободный член в этом уравнении,![]()
Решением
ЛСУ называется такая упорядоченная
совокупность чисел
![]() что при подстановке вместо
что при подстановке вместо
![]() соответственно
соответственно![]() в каждое уравнение системы все уравнения
обращаются в верные равенства. ЛСУ
называетсясовместной,
если существует хотя бы одно решение
системы (одна совокупность
в каждое уравнение системы все уравнения
обращаются в верные равенства. ЛСУ
называетсясовместной,
если существует хотя бы одно решение
системы (одна совокупность
![]() ),
в противном случае –несовместной.
),
в противном случае –несовместной.
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если имеет бесконечное множество решений.
Чтобы решить систему, сначала надо выяснить, совместна ли она. Для ответа на этот вопрос введем матричную запись ЛСУ.
Матрица
 (2.8)
(2.8)
составленная из коэффициентов при неизвестных ЛСУ, называется основной матрицей системы, а матрица
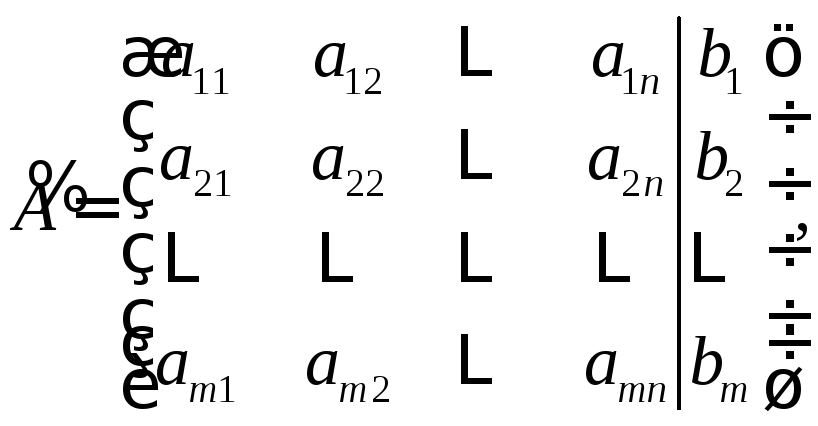 (2.9)
(2.9)
которая получается добавлением в матрицу А столбца из свободных членов, называется расширенной матрицей ЛСУ.
Введем также матрицы-столбцы

![]()
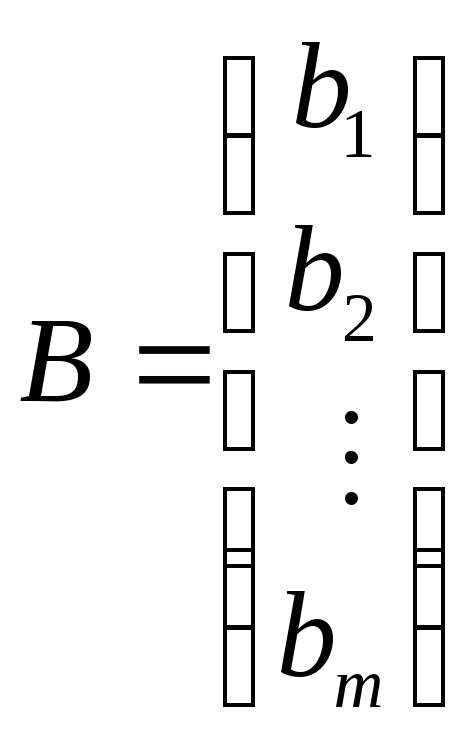 ,(2.10)
,(2.10)
где X и В – матрицы неизвестных и свободных членов.
Тогда, используя правило умножения матриц и определение равенства двух матриц, запишем ЛСУ в матричном виде:
![]() (2.11)
(2.11)
Теорема Кронекера
– Капелли.
Для совместности системы линейных
уравнений необходимо и достаточно,
чтобы r(A) =
![]() при этом, если
при этом, если
1)
![]() то система определена и имеет единственное
решение;
то система определена и имеет единственное
решение;
2) r < n, то система не определена и имеет бесконечное множество
решений.
Пример
7. Дана система
линейных уравнений:
Записать приведенную систему в матричном виде и исследовать ее на совместность.
Решение.
Введем основную и расширенную матрицы системы:
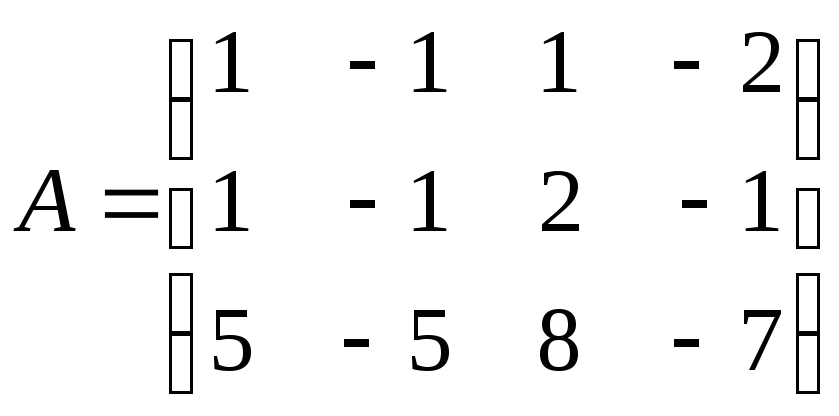 ;
;
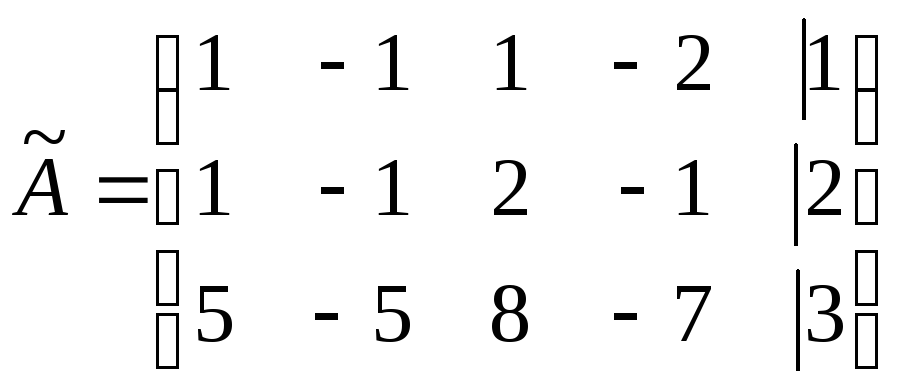 ,
матрицы-столбцы
,
матрицы-столбцы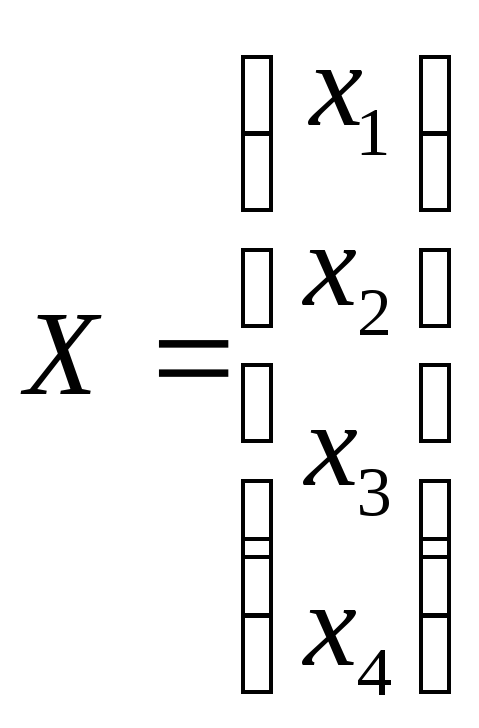 ;
; ,
тогда система запишется в виде матричного
уравнения:
,
тогда система запишется в виде матричного
уравнения:![]()
Для вычисления
r(А)
и
![]() выполним элементарные преобразования
над матрицей
выполним элементарные преобразования
над матрицей
![]() ,
так как матрицаА
является частью матрицы
,
так как матрицаА
является частью матрицы
![]() и
и![]() .
.
Столбец
из свободных членов в
![]() отделим вертикальной чертой и в процессе
преобразований не будем его менять
местами с другими столбцами матрицыА.
отделим вертикальной чертой и в процессе
преобразований не будем его менять
местами с другими столбцами матрицыА.
Выполняя элементарные
преобразования над матрицей
![]() описанные в подразд. 1.5, получаем:
описанные в подразд. 1.5, получаем:


 следовательно,
r(A)
= 2, r(
следовательно,
r(A)
= 2, r(![]() )
= 3 и система несовместна, т. е. не имеет
решений.
)
= 3 и система несовместна, т. е. не имеет
решений.
2.2. Методы решения систем линейных уравнений
Формулы Крамера
используются для решения системы,
основная матрица которой квадратная,
невырожденная (![]()
![]() ).
Названные формулы имеют вид:
).
Названные формулы имеют вид:
![]() (2.12)
(2.12)
где
![]() − главный определитель системы, т. е.
− главный определитель системы, т. е.
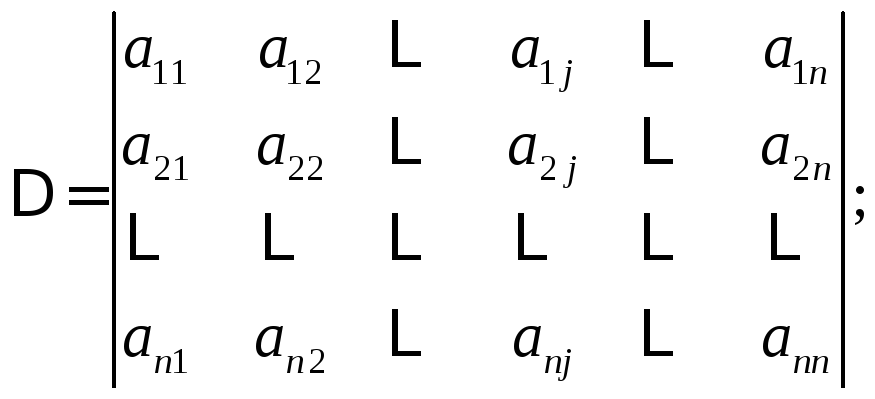 (2.13)
(2.13)
![]() −определители,
полученные из определителя
−определители,
полученные из определителя
![]() заменой в немj-го
столбца
заменой в немj-го
столбца
столбцом свободных членов, т. е.
 ;
;
 ,…;
,…;
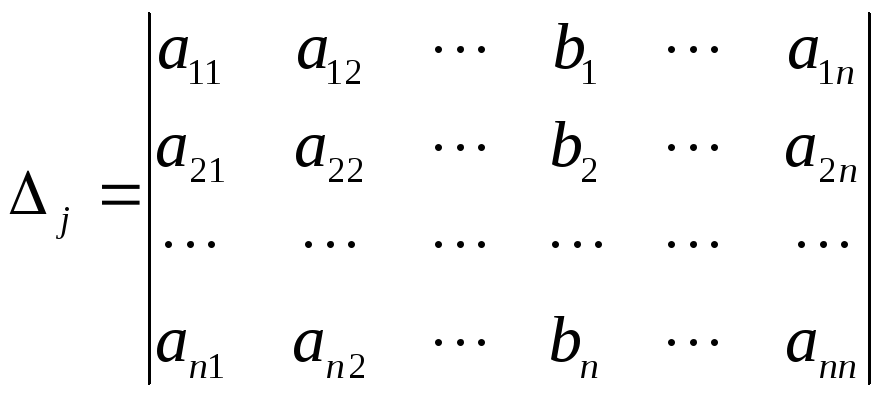 ,…;
,…;
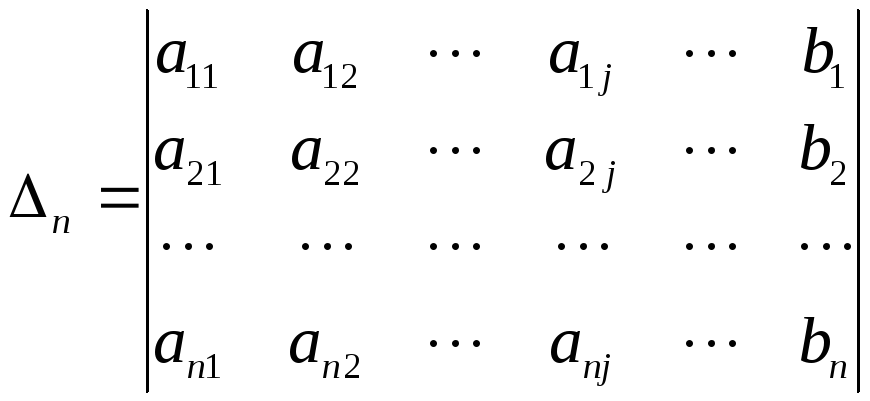 .
.
Пример
8. Решить
систему 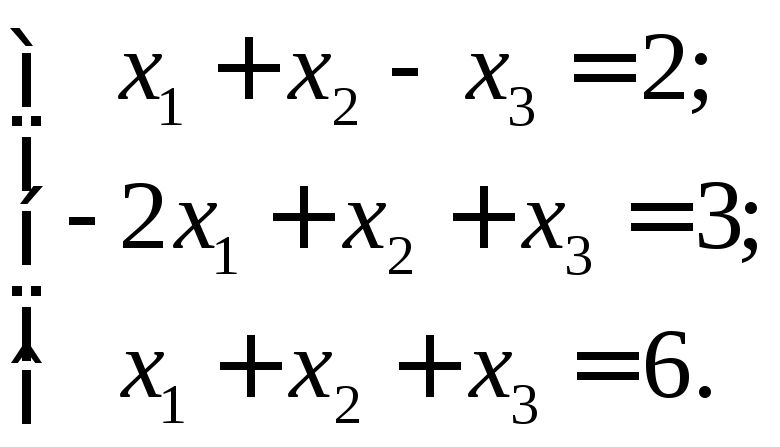 по формулам Крамера
и сделать проверку.
по формулам Крамера
и сделать проверку.
Решение.
Основная матрица
системы невырожденная, так как 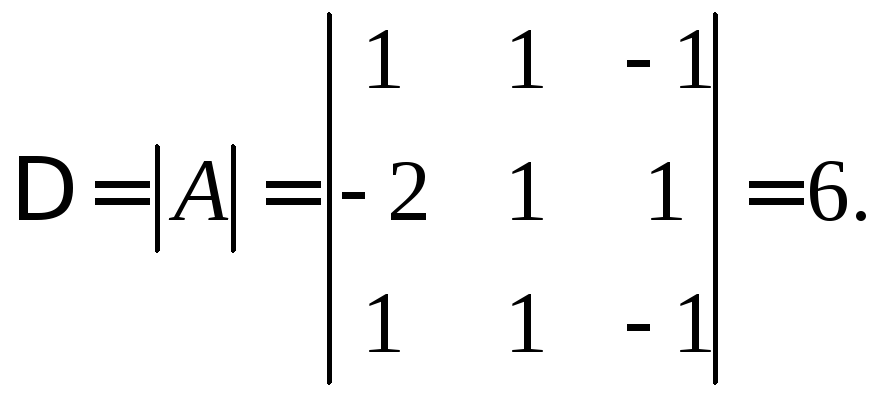 Определители
Определители![]() соответственно таковы:
соответственно таковы:
 ;
;
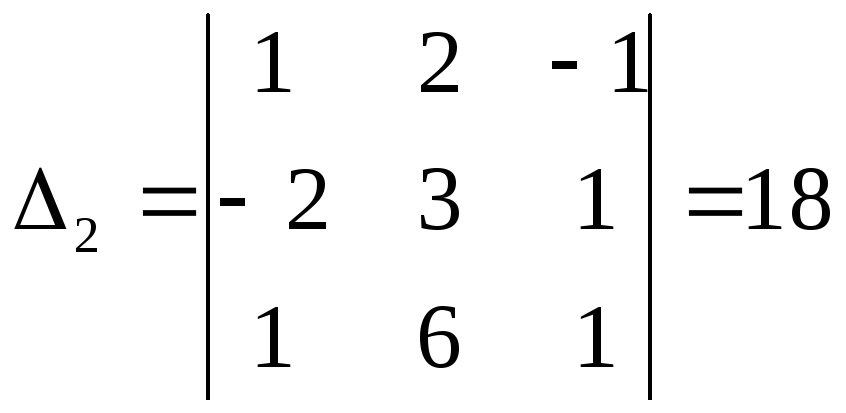 ;
; .
.
Применяя формулы
Крамера, находим неизвестные:
![]()
![]()
![]()
Подставляя найденные значения неизвестных в каждое уравнение системы, получаем верные равенства: 2 = 2, 3 = 3, 6 = 6.
Матричный метод
применяется для решения системы, основная
матрица которой квадратная, невырожденная
(m = n = r(A)
=![]() ).
В этом случае матричное уравнение
).
В этом случае матричное уравнение![]() приводится к виду:
приводится к виду:![]()
![]() .
.
Таким образом, чтобы решить систему матричным способом, необходимо записать ее в матричном виде, найти обратную матрицу к матрице А и умножить ее на матрицуВ.
Пример
9. Записать
систему  в матричном виде,
решить ее матричным способом, сделать
проверку.
в матричном виде,
решить ее матричным способом, сделать
проверку.
Решение.
Введем матрицы
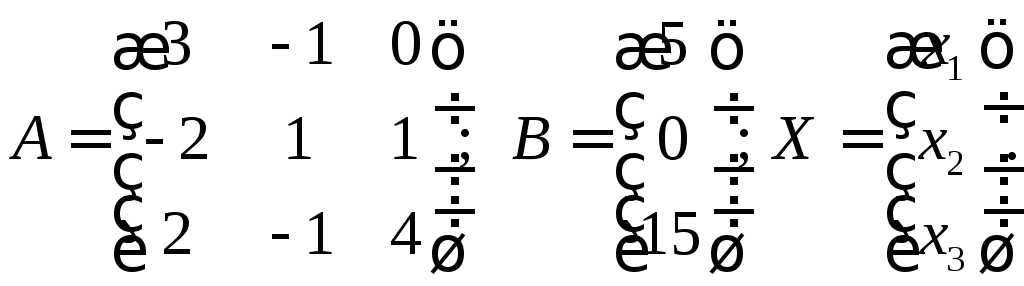 МатрицаА
невырожденная,
так как
МатрицаА
невырожденная,
так как
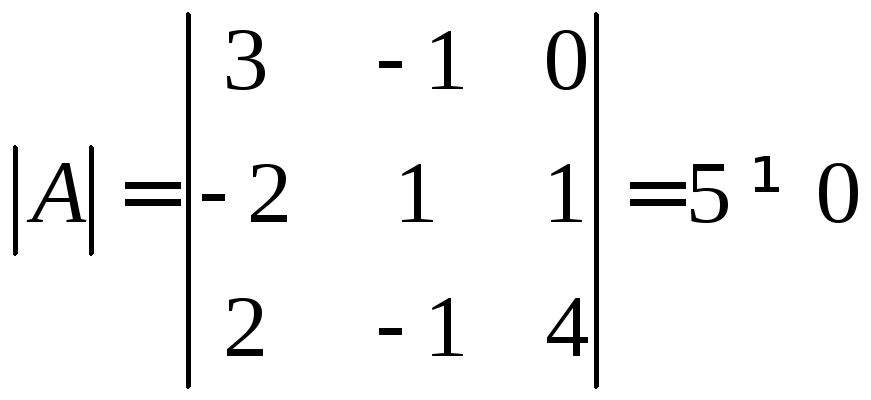 .
Найдем алгебраические дополнения для
каждого элемента матрицыА
(см. подразд.
1.2):
.
Найдем алгебраические дополнения для
каждого элемента матрицыА
(см. подразд.
1.2):
![]()
![]()
![]()
![]() Теперь запишем обратную матрицу:
Теперь запишем обратную матрицу: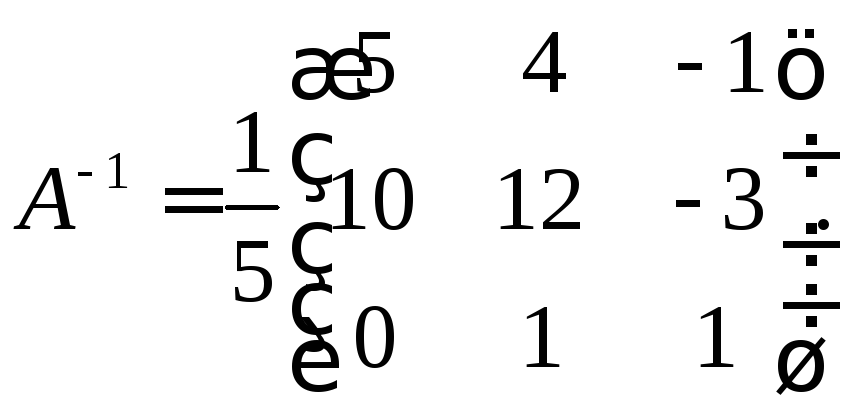
Подставляя
![]() иВ
в матричное уравнение
иВ
в матричное уравнение
![]() ,
получаем:
,
получаем:

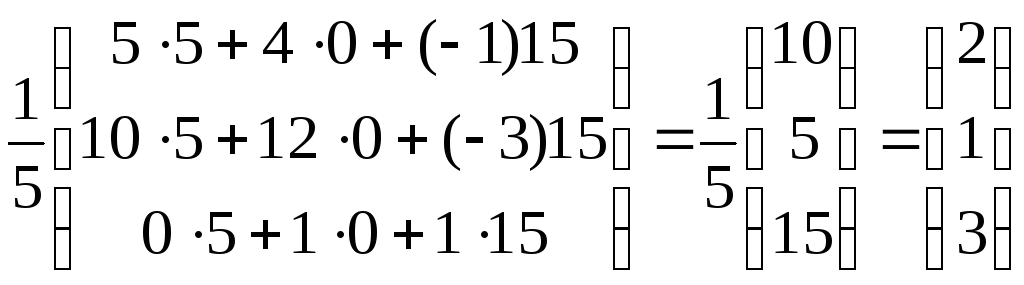 .
.
Значит,
![]()
![]()
![]()
Проверку решения можно выполнить, подставляя найденные значения неизвестных в каждое уравнение системы или используя матричное уравнение. Покажем, что АХ = В.
Действительно, умножая матрицу А на Х, получаем матрицу В:
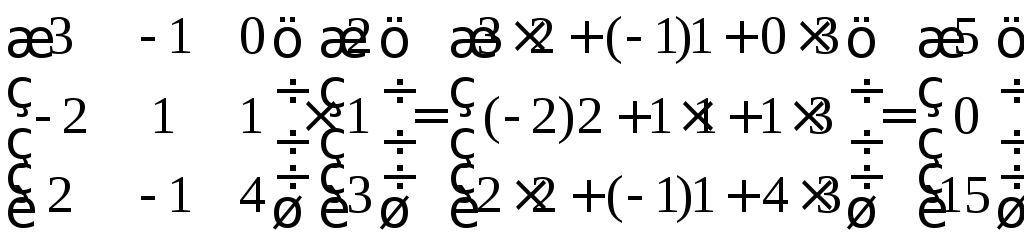 .
.
Метод Гаусса
(метод последовательного исключения
неизвестных) используется для решения
систем линейных уравнений произвольного
вида, т. е. для случаев, когда
![]() и
и![]()
Введем элементарные преобразования ЛСУ, которые приводят к эквивалентной системе, т. е. к системе, которая имеет такие же решения, что и исходная. К элементарным преобразованиям относятся:
умножение любого уравнения системы на число, отличное от нуля;
перестановка двух любых уравнений системы;
сложение одного уравнения системы с любым другим, умноженным на
произвольное число;
перенумерация неизвестных.
Очевидно, что
элементарные преобразования системы
соответствуют элементарным преобразованиям
над строками расширенной матрицы
![]() этой
системы. Перенумерация неизвестных
соответствует перестановке столбцов
основной матрицыА.
этой
системы. Перенумерация неизвестных
соответствует перестановке столбцов
основной матрицыА.
Если r
= n,
то с помощью указанных элементарных
преобразований расширенная матрица
![]() и система приводятся к треугольному
виду (прямой ход метода Гаусса):
и система приводятся к треугольному
виду (прямой ход метода Гаусса):
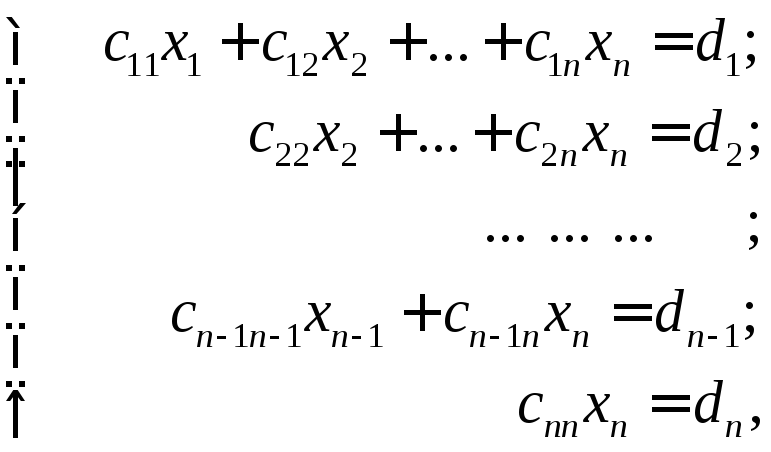 (2.14)
(2.14)
причем
![]()
Из последнего
уравнения системы (2.14) определяется
![]() .
Подставляя найденное
.
Подставляя найденное![]() в предпоследнее уравнение системы
(2.14), находим
в предпоследнее уравнение системы
(2.14), находим![]() .
Черезn
шагов определяются все неизвестные
системы (обратный ход метода Гаусса).
.
Черезn
шагов определяются все неизвестные
системы (обратный ход метода Гаусса).
Если
![]() ,
то с помощью элементарных преобразований
,
то с помощью элементарных преобразований![]() приводится к трапециевидной матрице
того же размера, что и
приводится к трапециевидной матрице
того же размера, что и
![]() ,в ней m
строк, из
них (
,в ней m
строк, из
них (![]() – нулевые, и (
– нулевые, и (![]() )
столбец, т. е. матрица
)
столбец, т. е. матрица![]() принимает вид:
принимает вид:
 ,(2.15)
,(2.15)
причем
![]()
По полученной матрице (2.15) восстанавливается ЛСУ:
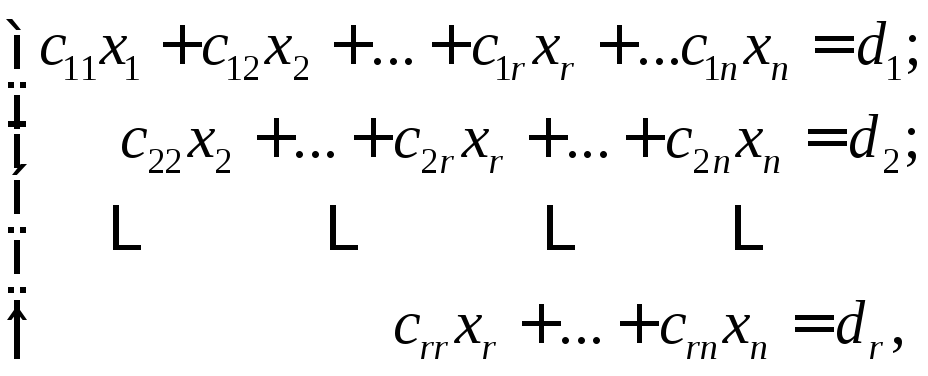 (2.16)
(2.16)
в которой r уравнений и n неизвестных. Полученная система (2.16), как и исходная, совместная, но неопределенная, т. е. имеет бесчисленное множество решений. Чтобы найти эти решения, перепишем систему уравнений (2.16) в виде:
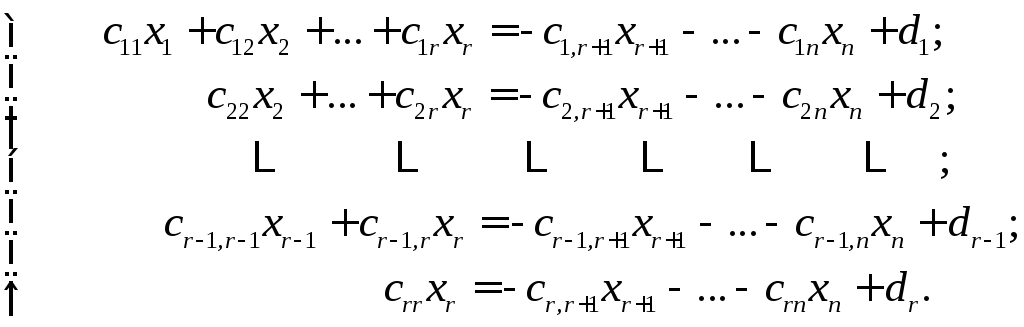 (2.17)
(2.17)
Неизвестные
![]() называютсябазисными,
коэффициенты при них образуют минор
r-го
порядка, отличный от нуля (базисный
минор).
Неизвестные
называютсябазисными,
коэффициенты при них образуют минор
r-го
порядка, отличный от нуля (базисный
минор).
Неизвестные
![]() называютсясвободными.
Придавая свободным неизвестным
произвольные значения, соответственно
называютсясвободными.
Придавая свободным неизвестным
произвольные значения, соответственно
![]() ,
найдем базисные неизвестные:
,
найдем базисные неизвестные:![]() −
из последнего уравнения полученной
системы (2.17);
−
из последнего уравнения полученной
системы (2.17);![]() − из предпоследнего и, наконец, черезr шагов
−
− из предпоследнего и, наконец, черезr шагов
−
![]() − из первого уравнения системы (2.17).
− из первого уравнения системы (2.17).
Пример
10. Дана
система линейных уравнений:
Требуется: 1) записать расширенную матрицу системы и привести ее к трапециевидной форме; 2) определить ранги основной и расширенной матриц системы и сделать вывод о совместности системы; 3) в случае, если система совместна, восстановить по трапециевидной расширенной матрице систему уравнений, эквивалентную исходной, и решить ее методом Гаусса; 4) сделать проверку решения.
Решение.
1) Запишем матрицу
![]() и с помощью элементарных преобразований
приведем ее к трапециевидной форме:
и с помощью элементарных преобразований
приведем ее к трапециевидной форме:
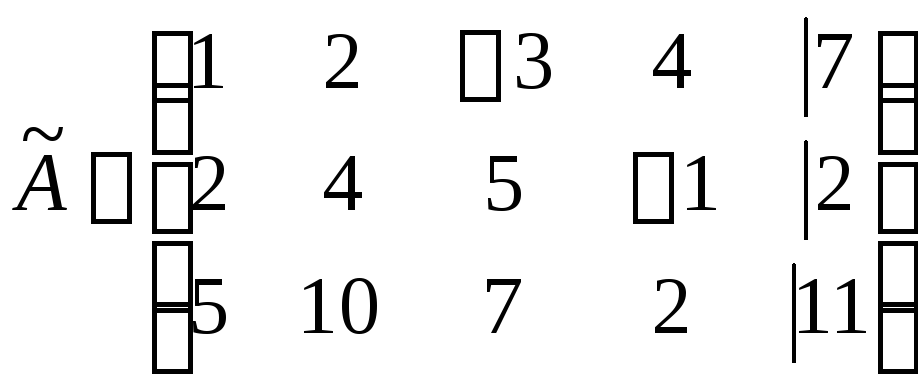 ~
~ ~
~ ~
~
~ .
.
2) Ранг основной матрицы равен двум, так как ее базисный минор
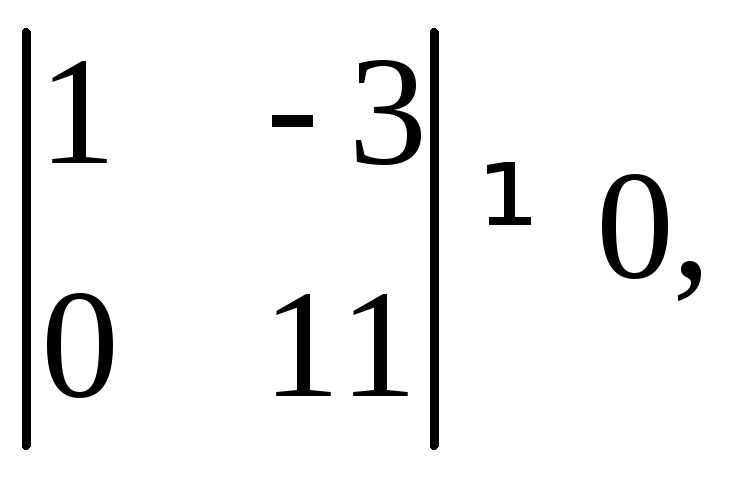 а все миноры
третьего порядка равны нулю. Ранг
расширенной матрицы также равен двум,
так как и для нее все миноры третьего
порядка, уже с учетом столбца свободных
членов, равны нулю. Следовательно,
система совместна.
а все миноры
третьего порядка равны нулю. Ранг
расширенной матрицы также равен двум,
так как и для нее все миноры третьего
порядка, уже с учетом столбца свободных
членов, равны нулю. Следовательно,
система совместна.
3) Восстановим по
трапециевидной расширенной матрице
систему уравнений, учитывая, что на
последнем шаге преобразований пришлось
переставлять второй и третий столбцы:
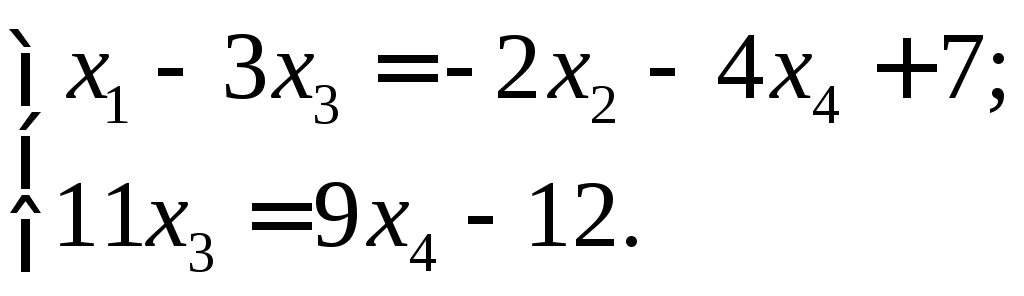
В системе четыре
неизвестных, а ранг равен двум,
следовательно,система
имеет бесчисленное множество решений
и два неизвестных являются свободными
(![]() ). Выбираем в качестве базисных неизвестных
). Выбираем в качестве базисных неизвестных![]() ,
,![]() ,
тогда
,
тогда![]() будут свободными неизвестными. Перепишем
систему в виде:
будут свободными неизвестными. Перепишем
систему в виде:
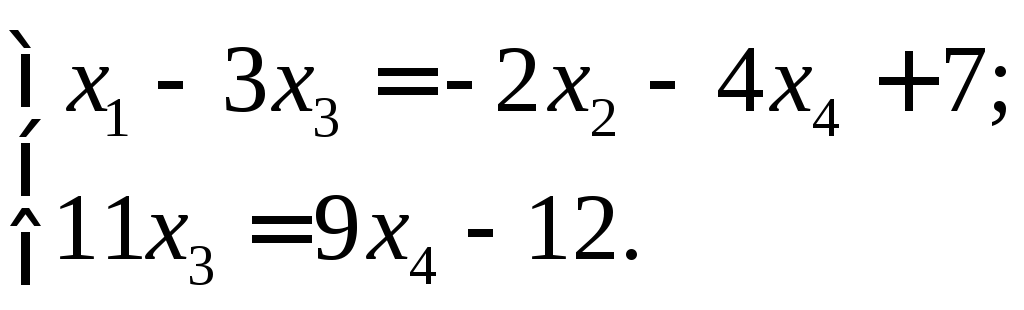 (2.18)
(2.18)
Пусть![]() ,
где
,
где![]() – любые числа, тогда из последнего
уравнения системы (2.12) получаем:
– любые числа, тогда из последнего
уравнения системы (2.12) получаем:![]() .
Подставляя найденное
.
Подставляя найденное![]() в первое уравнение системы (2.12), находим
в первое уравнение системы (2.12), находим![]() .
.
4) Для проверки
подставляем найденные значения
![]() в исходную систему уравненийи получаем верные равенства:
в исходную систему уравненийи получаем верные равенства:

Следовательно, множество решений системы имеет вид:
 .
.
