Задание 6

Требуется рассчитать средние значения , дисперсии D(y)и средние квадратические отклоненения проката при нескольких значениях пробега, пользуясь зависимостями (14) и (15), полученными при решении задания 5. Затем требуется для тех же значений пробега определить нижнюю y(t)_min и верхнюю y(t)_max границы практически возможных значений проката. Результаты расчетов следует занести в таблицу, выполненную по форме табл.6, и построить по ним линии, представляющие собой зависимость среднего проката бандажей от пробега, нижнюю и верхнюю границы практически возможных значений проката.

Таблица 6

Результаты расчета средних значений, дисперсий и средних

квадратических отклонений проката бандажей

№ п/п	Наименование показателя	Пробег, тыс. км
		0	50	100	…	300	350
1	Средний прокат , мм	…	…	…	…	…	…
2	Дисперсия проката D(y), мм2	…	…	…	…	…	…
3	Среднее квадратическое отклонение проката (y), мм	…	…	…	…	…	…
4	Утроенное значение 3(y), мм	…	…	…	…	…	…
5	Нижняя граница y(t)min, мм	…	…	…	…	…	…
6	Верхняя граница y(t)max, мм	…	…	…	…	…	…

Предельное значение y_пр проката бандажей колесных пар грузовых тепловозов установлено равным 7 мм, а пассажирских тепловозов - 5 мм. Заданная серия тепловоза указана в табл.7.

Таблица 7

Заданная серия тепловоза

Последняя цифра шифра	0	1	2	3	4
Серия тепловоза	ТЭП60	2ТЭ10М	ТЭП70	2ТЭ116	2ТЭП60
Последняя цифра шифра	5	6	7	8	9
Серия тепловоза	2ТЭ121	2ТЭ10Л	2ТЭ10У	2ТЭ10В	ТЭ3

Методические указания. Заполните таблицу формы 6, последовательно производя вычисления по формулам (14) и (15), полученным при выполнении задания 5, для значений пробега локомотива от 0 до 350 тысяч километров через 50 тыс. км. Расчет средних квадратических отклонений произведите по формуле:

.

Принятой модели процесса износа бандажа, определяемой выражениями (14) и (15), соответствует такое постепенное увеличение проката, при котором среднее значение и дисперсия приращения проката за некоторый интервал пробега Δt пропорциональны длине этого интервала и не зависят от достигнутого значения y. В таком случае вполне допустимо, основываясь на основных теоремах теории вероятностей, считать, что для любого t (пока y < y_пр ) значения проката распределены по нормальному закону с плотностью распределения:

.

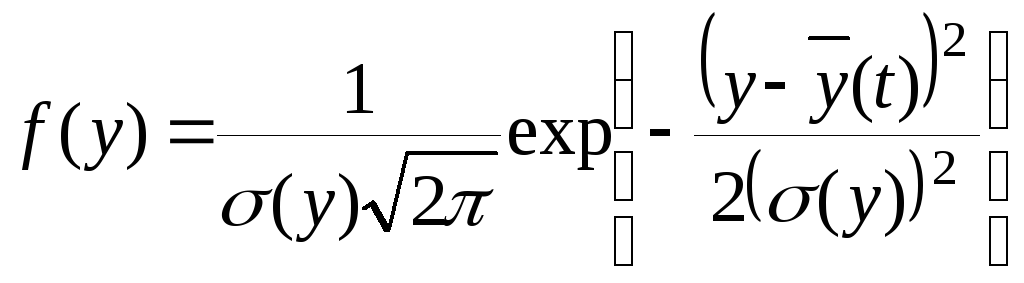Сужение области определения функции до интервала [0,y_пр] практически не оказывает влияния на результаты расчетов.

Для нахождения области практически возможных значений случайной величины, распределенной по нормальному закону, пользуются "правилом трех сигма". В соответствии с этим правилом для каждого пробега локомотива t верхняя и нижняя границы практически возможных значений проката бандажей находятся как:

, (20)

. (21)

Полученные зависимости иллюстрирует рис.4.

Рис.4

По результатам расчетов, сведенным в табл.6, постройте график зависимости среднего проката бандажей от пробега (рис.4). Проведите на графике прямую y=y_ПР. Пользуясь данными табл. 6, постройте на этом же графике кривые, показывающие верхнюю и нижнюю границы практически возможных значений проката бандажей. Покажите на графике обе исходные точки (t₁, ), (t₂, )и отметьте их координаты.

При построении графика рекомендуется использовать следующий масштаб: пробег – в 1 мм 1 тыс.км, прокат - в 1 мм 0,05 мм проката.

Контрольный вопрос. Имеет ли смысл при заданных условиях вычислять значения среднего проката и дисперсии проката для наработки t=360 тыс.км и более?