5.3.Формирование математической модели и программного модуля расчета функция изменения температуры
Рассмотрим методику формирования аппроксимирующих зависимостей на примере функции изменения температуры для стандартной атмосферы.
На рис.1.дана система исходных точек для функции изменения температуры от высоты. Вид зависимостей показывает, что описать одной функцией представленную совокупность точек в достаточно высокой точность невозможно. Поэтому, делим весь диапазон высот на два отдельных участка, для которых и будем формировать аппроксимирующие зависимости.
Рис.1. Табулированные значения для температурной функции стандартной атмосферы
В табл.3 представлен вид такой таблицы с выделение отдельных диапазонов. С целью сокращения объемов таблиц данные по диапазонам в отдельные столбцы выделять не будем, а будем используем двух или трех блочное построение таблицы (см.табл.4 в зависимости от количества диапазонов). Выбор блоков данных для графических построений выполним при формировании рядов исходных данных диаграмм. Таблица содержат так же интересующие нас расчетные данные для значений функции и величины погрешностей. В таблицу введены в начале блока для каждого диапазона строки, содержащие ссылку на модель и уравнение полученной регрессионной модели.
На рис.2 показан вариант формирования математической модели ав форме двух квадратичных полиномов на двух примыкающих диапазонах данных.
Рис.2. Аппроксимации температурной функции двумя квадратичными полиномами
Следует отметить, что несмотря на достаточно хорошие результаты аппроксимации, полученная математическая модель для практического применения не удобна. Это связано с тем, что численные значения двух коэффициентов в каждом полиноме существенно меньше 1 и для обеспечения высокой точности потребуется увеличить количество значащих цифр после десятичного разделителя. Это связано с тем, что при использовании в качестве независимой переменной высоты, заданной в км, чувствительность к ее изменению незначительна. Чувствительность к изменению высоты можно существенно повысить, если в качестве независимой переменной применить высоту, заданную в сотнях км( нормировка высоты).
Полученные данные для новой переменной модели представлены на рис.3 и в табл.5. Для первого диапазоны высот выбран полином 6-ой степени, что обусловлено наличием точек перегиба в зависимости. Для 2-го диапазона - полином 2-ой степени.
Таблица 3. Формирование диапазонов для расчета функции температуры
|
Высота,км, |
Изменение температуры, √T(0)/T(h) |
h(0;50) |
h(50;100) |
|
0 |
1 |
1 |
|
|
0,5 |
1,003 |
1,003 |
|
|
1 |
1,01 |
1,01 |
|
|
1,5 |
1,015 |
1,015 |
|
|
2 |
1,021 |
1,021 |
|
|
3 |
1,032 |
1,032 |
|
|
5 |
1,054 |
1,054 |
|
|
6,5 |
1,072 |
1,072 |
|
|
10 |
1,118 |
1,118 |
|
|
15 |
1,133 |
1,133 |
|
|
20 |
1,133 |
1,133 |
|
|
25 |
1,121 |
1,121 |
|
|
30 |
1,109 |
1,109 |
|
|
35 |
1,098 |
1,098 |
|
|
40 |
1,034 |
1,034 |
|
|
45 |
0,979 |
0,979 |
|
|
50 |
0,933 |
0,933 |
0,933 |
|
55 |
0,963 |
|
0,963 |
|
75 |
1,122 |
|
1,122 |
|
100 |
1,176 |
|
1,176 |
Таблица 4. Аппроксимация температурной функции квадратичными полиномами
|
Модель |
y = -0,00028x2 + 0,01217x + 1,00115 | |||
|
Высота,км, |
Изменение температуры, √T(0)/T(h) |
yрегр |
Δy |
Δy,% |
|
0 |
1 |
1,00115 |
0,00115 |
0,11% |
|
0,5 |
1,003 |
1,007165 |
0,004165 |
0,42% |
|
1 |
1,01 |
1,01304 |
0,00304 |
0,30% |
|
1,5 |
1,015 |
1,018775 |
0,003775 |
0,37% |
|
2 |
1,021 |
1,02437 |
0,00337 |
0,33% |
|
3 |
1,032 |
1,03514 |
0,00314 |
0,30% |
|
5 |
1,054 |
1,055 |
0,001 |
0,09% |
|
6,5 |
1,072 |
1,068425 |
-0,003575 |
-0,33% |
|
10 |
1,118 |
1,09485 |
-0,02315 |
-2,07% |
|
15 |
1,133 |
1,1207 |
-0,0123 |
-1,09% |
|
20 |
1,133 |
1,13255 |
-0,00045 |
-0,04% |
|
25 |
1,121 |
1,1304 |
0,0094 |
0,84% |
|
30 |
1,109 |
1,11425 |
0,00525 |
0,47% |
|
35 |
1,098 |
1,0841 |
-0,0139 |
-1,27% |
|
40 |
1,034 |
1,03995 |
0,00595 |
0,58% |
|
45 |
0,979 |
0,9818 |
0,0028 |
0,29% |
|
50 |
0,933 |
0,90965 |
-0,02335 |
-2,50% |
|
| ||||
|
Модель |
y = -0,00011x2 + 0,02113x + 0,13651 | |||
|
|
Изменение температуры, √T(0)/T(h) |
yрегр |
Δy |
Δy,% |
|
50 |
0,933 |
0,91801 |
-0,01499 |
-1,61% |
|
55 |
0,963 |
0,96591 |
0,00291 |
0,30% |
|
75 |
1,122 |
1,10251 |
-0,01949 |
-1,74% |
|
100 |
1,176 |
1,14951 |
-0,02649 |
-2,25% |
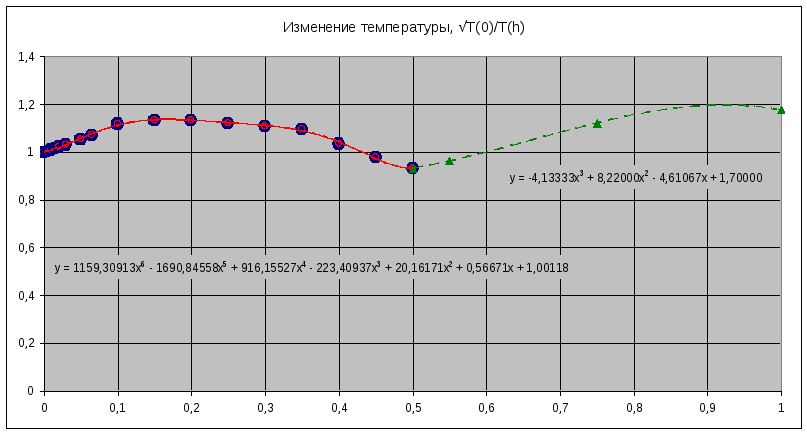
Рис.3. Аппроксимации температурной функции двумя полиномами после нормировки h
Таблица 5. Аппроксимация температурной функции полиномами после нормировки высоты
|
Модель |
y= 1159,30913x6 - 1690,84558x5 + 916,15527x4 - 223,40937x3 + 20,16171x2 + 0,56671x + 1,00118 | |||
|
Высота/100,км |
Изменение температуры, √T(0)/T(h) |
yрегр |
Δy |
Δy,% |
|
0 |
1 |
1,00118 |
0,00118 |
0,12% |
|
0,005 |
1,003 |
1,00449 |
0,00149 |
0,15% |
|
0,01 |
1,01 |
1,008649 |
-0,001351 |
-0,13% |
|
0,015 |
1,015 |
1,013508 |
-0,001492 |
-0,15% |
|
0,02 |
1,021 |
1,018933 |
-0,002067 |
-0,20% |
|
0,03 |
1,032 |
1,030997 |
-0,001003 |
-0,10% |
|
0,05 |
1,054 |
1,057209 |
0,003209 |
0,30% |
|
0,065 |
1,072 |
1,076325 |
0,004325 |
0,40% |
|
0,1 |
1,118 |
1,111925 |
-0,006075 |
-0,54% |
|
0,15 |
1,133 |
1,134429 |
0,001429 |
0,13% |
|
0,2 |
1,133 |
1,132689 |
-0,000311 |
-0,03% |
|
0,25 |
1,121 |
1,122743 |
0,001743 |
0,16% |
|
0,3 |
1,109 |
1,110933 |
0,001933 |
0,17% |
|
0,35 |
1,098 |
1,089196 |
-0,008804 |
-0,80% |
|
0,4 |
1,034 |
1,043384 |
0,009384 |
0,91% |
|
0,45 |
0,979 |
0,974634 |
-0,004366 |
-0,45% |
|
0,5 |
0,933 |
0,933776 |
0,000776 |
0,08% |
|
| ||||
|
Модель |
y == -4,13333x3 + 8,22000x2 - 4,61067x + 1,70000 | |||
|
|
Изменение температуры, √T(0)/T(h) |
yрегр |
Δy |
Δy,% |
|
0,5 |
0,933 |
0,932999 |
-1,25E-06 |
0,00% |
|
0,55 |
0,963 |
0,962999 |
-1,28E-06 |
0,00% |
|
0,75 |
1,122 |
1,121999 |
-1,09E-06 |
0,00% |
|
1 |
1,176 |
1,176 |
0 |
0,00% |
Полученные в расчетах данные показывают, что погрешность математической модели не превышает 0,54% в диапазоне высот от 0км до 30км и от 50км до 100км, а в диапазоне от 35км до 45км погрешность модели не превышает 1%.
Изменение вида уравнения тренда не может привести к увеличению точности модели, что связано со сложным характером температурной зависимости в диапазоне изменения высоты от 25км до 50км и невозможность сформировать общие закономерности для разнотипных зависимостей. С целью увеличения точности модели введем в расчет три диапазона высот:
от 0км до 10км;
от 20км до 55км;
от 55км до 100км.
Повторяем расчеты для варианта расчетов с тремя кусочно-полиномиальными моделями. Результаты представлены в табл.6 и рис.4.
Таблица 6. Аппроксимация температурной функции полиномами для 3-х диапазонов
|
Модель |
y= 1,71164x2 + 1,01256x + 0,99943 | |||
|
Высота/100,км |
Изменение температуры, √T(0)/T(h) |
yрегр |
Δy |
Δy,% |
|
0 |
1 |
0,99943 |
-0,00057 |
-0,06% |
|
0,005 |
1,003 |
1,004536 |
0,001536 |
0,15% |
|
0,01 |
1,01 |
1,009727 |
-0,000273 |
-0,03% |
|
0,015 |
1,015 |
1,015004 |
3,52E-06 |
0,00% |
|
0,02 |
1,021 |
1,020366 |
-0,000634 |
-0,06% |
|
0,03 |
1,032 |
1,031347 |
-0,000653 |
-0,06% |
|
0,05 |
1,054 |
1,054337 |
0,000337 |
0,03% |
|
0,065 |
1,072 |
1,072478 |
0,000478 |
0,04% |
|
0,1 |
1,118 |
1,117802 |
-0,000198 |
-0,02% |
|
| ||||
|
Модель |
y = 284,30769x5 - 408,55012x4 + 219,46061x3 - 56,58469x2 + 6,98078x + 0,8043 | |||
|
Высота/100,км |
Изменение температуры, √T(0)/T(h) |
yрегр |
Δy |
Δy,% |
|
0,1 |
1,118 |
1,11798 |
-2,02E-05 |
0,00% |
|
0,15 |
1,133 |
1,133702 |
0,000702 |
0,06% |
|
0,2 |
1,133 |
1,130052 |
-0,002948 |
-0,26% |
|
0,25 |
1,121 |
1,123769 |
0,002769 |
0,25% |
|
0,3 |
1,109 |
1,11296 |
0,00396 |
0,36% |
|
0,35 |
1,098 |
1,087754 |
-0,010246 |
-0,93% |
|
0,4 |
1,034 |
1,040968 |
0,006968 |
0,67% |
|
0,45 |
0,979 |
0,978767 |
-0,000233 |
-0,02% |
|
0,5 |
0,933 |
0,931327 |
-0,001673 |
-0,18% |
|
0,55 |
0,963 |
0,963492 |
0,000492 |
0,05% |
|
| ||||
|
Модель |
y= -1,0728x2 + 2,1132x + 0,1365 | |||
|
|
Изменение температуры, √T(0)/T(h) |
yрегр |
Δy |
Δy,% |
|
0,55 |
0,963 |
0,962999 |
-1,28E-06 |
0,00% |
|
0,75 |
1,122 |
1,121999 |
-1,09E-06 |
0,00% |
|
1 |
1,176 |
1,176 |
0 |
0,00% |
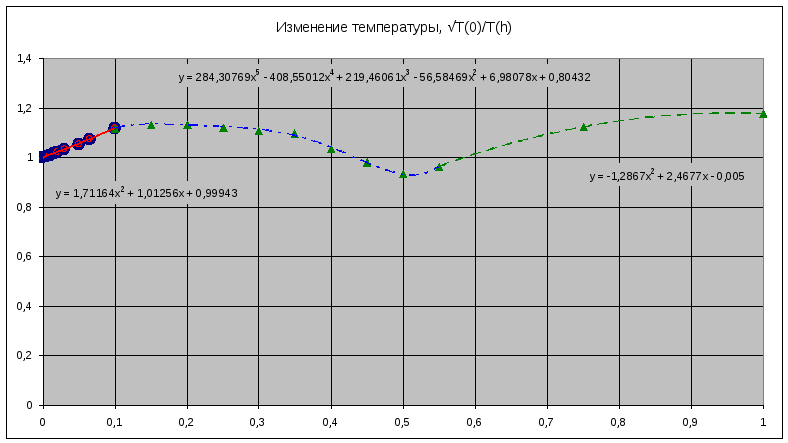
Рис.4.Аппроксимация температурной функции полиномами для 3-х диапазонов