Лекция №5 Симметрия кристаллов. Системы трансляции.

При изучении внешних форм монокристаллов обычно сразу становится заметным, что большая часть их обладает симметрией.

Считается, что геометрическая фигура обладает симметрией, если при совершении какой-либо геометрической операции, например при вращении вокруг некоторой оси или отражения в какой-либо плоскости, она совпадает с исходным положением (см. рисунок)

Если кристалл по внешней форме рассматривать как многогранник, то в нем можно встретить следующие элементы симметрии: оси симметрии 2-го, 3-го, 4-го, и 6-го порядка (оси 5-го и 6-го порядка не встречаются), зеркально поворотные оси, плоскости симметрии и центр симметрии. Про какую либо фигуру говорят, что она обладает осью симметрии 6-го порядка, когда совмещается сама с собой при вращении вокруг этой оси на угол 2π/6. Как показывает математический анализ, комбинирование элементов симметрии подчиняется строгим законам т.е. не любые комбинации возможны.

Установлено, что возможны лишь 32 комбинации элементов симметрии; им соответствует 32 кристаллических класса, или класса симметрии.

Так например, куб имеет следующие элементы симметрии:

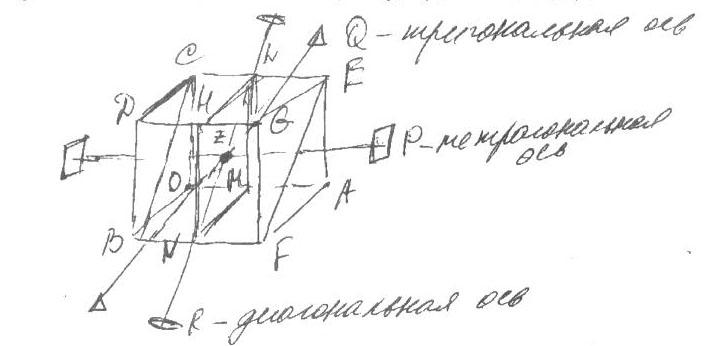
а) вращение вокруг оси Р, проходящей через центр и нормали к двум плоскостям куба, которые при повороте на 90° приводит с совмещению фигуры; следовательно, это ось 4-го порядка (тетролональная). Таких осей в кубе три. Обозначив их черех С, можно записать 3С₄ (читается: три оси четвертого порядка).

б) диагональ куба Q – ось 3-го порядка (тригональная), а их в кубе можно провести 4, т.е символ 4C₃.

в) ось, проходящая через середины противоположных рёбер R, будет осью 2-го порядка (диагональная) всего ребер в кубе двенадцать, а осей таких шесть,

т.е. символ 6С₂.

г) можно провести три плоскости LHMN через середины рёбер и шесть диагональных плоскостей типа BCEF, т.е. всего 9P.

д) один центр симметрии, обозначение через Z.

Таким образом, куб имеет следующие элементы симметрии:

3C4, 4c3, 6c2, 9p, 1z.

Однако есть кубические кристаллы, не обладающие столь высокой симметрией. Есть класс, относящийся к кубической системе, который имеет только тройные и двойные оси симметрии: 4С₃ и 3С₂.

Необходимый признак принадлежности кристалла к кубическому классу – наличие четырех осей 3-го порядка, а для гексалональных – наличие осей

6-го порядка.

Очевидно, простая ячейка той или иной системы обладает наибольшем числом элементов симметрии (голоэдрический класс), а при переходе к сложным решеткам число элементов симметрии может понижаться (гомоэдрические классы).

Однако не любая сложная решетка приводит к понижению симметрии.

Например, если частицы находятся в центре куба или на серединах его граней, то от этого число элементов симметрии не уменьшается

(следовательно эти решетки являются голоэдрическими).

Системы трансляции (решётки Браве).

Как мы уже установили, кристаллические решетки можно разбить на семь семейств сообразно трем осевым углам и трем осевым трансляциям. Однако одну и ту же решетку можно описать с помощью разных осевых трансляций. Поясним сказанное примером.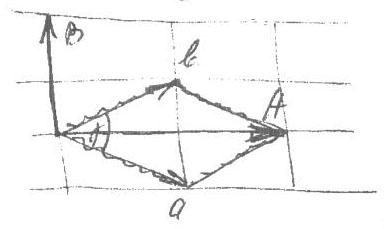

Для простоты возьмем плоскую фигуру. Как видно из рисунка систему точек, лежащих в вершинах ромба, можно описать с помощю векторов а, в (равных по модулю) и осевого угла γ, который отличен от 90°. Теперь попытаемся описать эту же фигуру в ортоганальной системе координат. Для этого выберем трансляции A и В, равные соответственно а+в и а-в. Однако так не получается вершина лежащая в точке в, т.е. в середине большой элементарной петли.

-26-

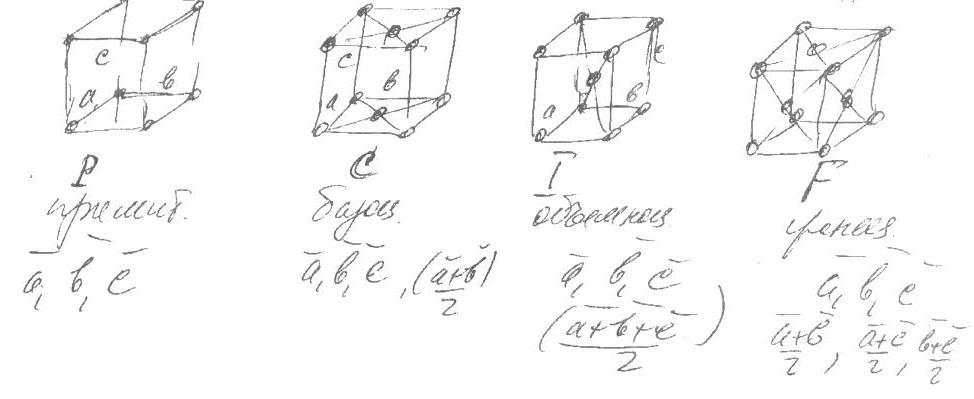
Для трансляции этой точки надо задать ей самостоятельную трансляцию (А+В)/2. Таким образом в ортоганальных координатах системой трансляции для этой ячейки будет А, В и (А+В)/2. В итоге для одной фигуры, или для одной элементарной ячейки мы предложим две разные системы. Системы трансляций прнято называть решетками Бравэ. Показано, что решеток Бравэ может быть всего 14, которые по-разному распределяются по сингониям. Решетки Бравэ могут быть примитивными (если они заданы трансляциями а, в и е, обозначаются символом Р), базоцентрироваными, задающиеся трансляциями а, в, с и (а+в)/2 (обозначены символом С), обьемноцентрированными ( I ), задающиеся трансляциями a,в,с и (а+в+с)/2 и гранецентрированными (F) с пучком трансляций а,в,с (ав/2), (ас/2), (вс/2).

Системы трансляций.

Система кристаллов	Система трансляций	Символ
Триклинная	Примитивная	P
Моноклинная	Примитивная Базоцентрированная	P C
Ромбическая	Примитивная Базоцентрированная Обьемноцентрированная Гранецентрированная	P C I F
Тригональная (ромбическая)	Примитивная	P
Тетрогональная	Примитивная Обьемноцентрированная	P I
Гексогональная	Примитивная	P
Кубическая	Примитивная Обьемноцентрированная Гранецентрированная	P I F

В качестве примера изобразим решетки Бравэ для ромбической системы