процессы -гидравлические / гидравлические / гидравлические / 1.5. Потери энергии при движении жидкости (1 часть)

1.5. Потери энергии при движении жидкости

Характер и виды потерь энергии. Ламинарный и турбулентный режимы движения. Получение конкретных зависимостей для расчета потерь энергии при движении жидкости в трубах и каналах является основным содержанием внутренней задачи гидродинамики. Различают два вида потерь энергии при установившемся напорном движении жидкости: потерю энергии по длине h_l и местные потери энергии, каждую из которых обозначим h_мс.

К потере энергии по длине относится та часть энергии потока, которая расходуется на преодоление трения в прямолинейных участках труб и каналов, где движение жидкости равномерное или плавноизменяющееся. Эта энергия переходит в теплоту и безвозвратно теряется потоком.

К местной потере энергии относится та часть энергии потока, которая расходуется также на преодоление трения, но в местах, где поток претерпевает резкую деформацию. В результате на некотором сравнительно небольшом участке нарушается равномерное движение жидкости, ее скорость изменяется по величине и направлению. Деформация потока (нарушение его нормальной конфигурации) имеет место при его входе в трубу, при резком расширении и сужении трубопровода, в местах, где установлены вентили, краны, при поворотах трубы и т. п.

П

Рис. 1.38. Трубопровод с участками местных сопротивлений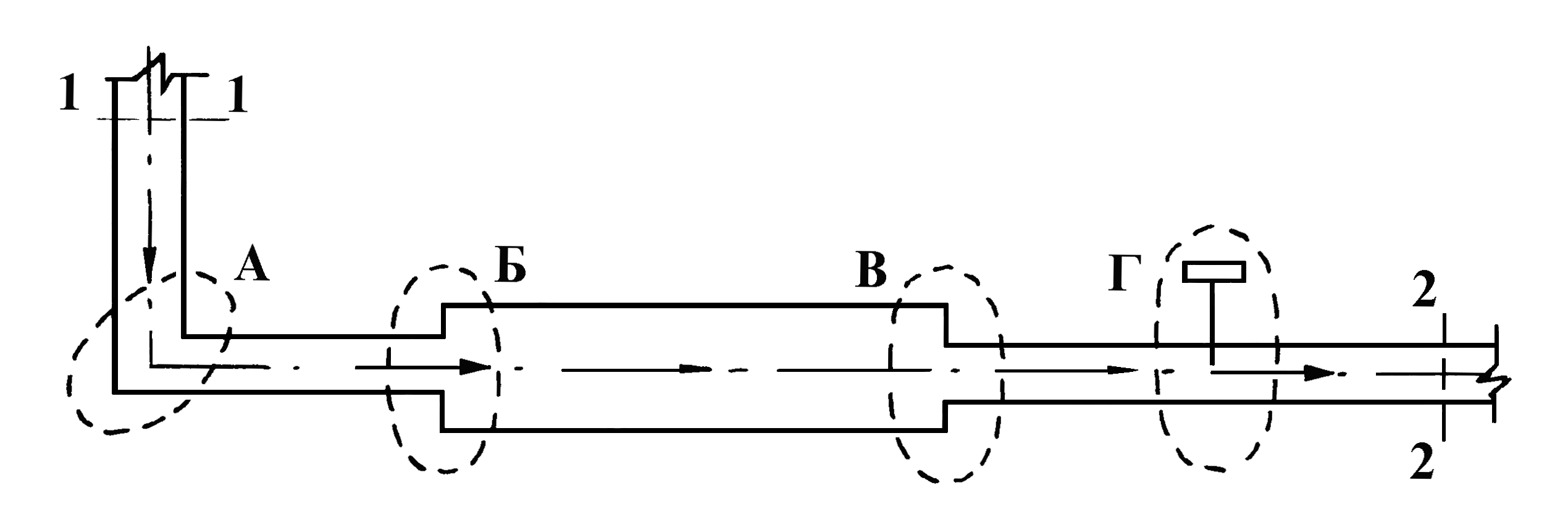

редставим поток в трубопроводе (Рис. 1.38), включающем участки: поворот А; резкое расширение Б; резкое сужение В; задвижку Г (частично открытую).

Помимо потерь энергии по длине между сечениями 1-1 и 2-2 в данном случае будут еще четыре местные потери энергии.

В общем случае для участка потока в трубе, заключенного между двумя сечениями, полная потеря энергии

. (1.146)

Чтобы определить величину касательных напряжений, обусловливающих потери энергии, необходимо изучить режимы движения жидкости (ламинарный и турбулентный).

При ламинарном (от лат. lamina  слой) движении отдельные частицы жидкости в трубе перемещаются по прямолинейным траекториям параллельно стенкам трубы и друг другу. Никаких поперечных перемещений частиц не происходит. Иначе говоря, жидкость в круглой трубе движется как бы концентрическими кольцевыми слоями, которые не перемешиваются между собой.

При турбулентном (от лат. turbulentus  неупорядоченный, бурный) движении отдельные частицы жидкости или целые группы частиц конечных размеров («жидкие комки») ведут себя приблизительно как молекулы по представлениям кинетической теории газов, т. е. пребывают в состоянии хаотичного движения. Поскольку поток в целом движется прямолинейно, «жидкие комки» наряду с общим поступательным движением имеют и случайные поперечные перемещения; во всем потоке происходит процесс непрерывного перемешивания частиц жидкости.

Турбулентный поток по своим свойствам резко отличается от ламинарного. При ламинарном режиме потери энергии по длине пропорциональны первой степени скорости, при турбулентном  приблизительно квадрату скорости.

Условия перехода от ламинарного течения капельной жидкости к турбулентному и,наоборот в круглых трубах впервые в 1883-1885 гг. изучил английский ученый О. Рейнольдс. Он установил, что этот переход определяется четырьмя физическими величинами: средней скоростью течения , диаметром трубы d, вязкостью жидкости  и ее плотностью , составляющими безразмерный комплекс, получивший название критерия (числа) Рейнольдса Re.

В своих исследованиях Рейнольдс пришел к выводу, что существует некоторое критическое значение Re_кр, являющееся границей между ламинарным и турбулентным режимами течения, и нашел его: Re_кр = 2320.

При Re>2320 движение будет турбулентным, а при Re<2320  ламинарным.

Более тщательные исследования, выполненные в последние годы, свидетельствуют о том, что в практике нередко встречаются с течениями, когда в потоках есть ламинарные и турбулентные участки. При возрастании числа Re и приближении его к критическому в ламинарном потоке образуются очаги, имеющие турбулентный характер. Это явление называется перемежаемостью. Ее характеристикой является коэффициент перемежаемости =, выражающей долю времени существования турбулентного режима в рассматриваемой точке пространства. При полностью ламинарном течении = 0, при полностью турбулентном = 1.

Перемежающая турбулентность существует в пределах изменения числа Рейнольдса от 2000 до 4000, поэтому более точные условия существования ламинарного и турбулентного режимов течения в трубах следующие: Re  2000  ламинарный режим, Re > 4000  турбулентный режим. Критическое значение числа Рейнольдса зависит от структуры потока, наличия примесей. Значения чисел Рейнольдса (Re  2000 и Re > 4000)относятся к равномерному течению чистых жидкостей и газов в трубах. При неравномерном движении на значение Re_кр существенно влияет характер изменения скоростей вдоль течения. Например, в сужающихся трубах (конфузорах), где скорость возрастает по течению и само течение более устойчиво, нижнее значение Re_кр резко возрастает (до 20000 для труб круглого сечения). В расширяющихся трубах (диффузорах), где скорость уменьшается по течению, переход от турбулентного режима к ламинарному происходит при Re_кр < 2000.

Решение уравнения движения вязкой жидкости НавьеСтокса для ламинарного режима: законы Стокса, Гагена-Пуазейля, формулы Дарси-Вейсбаха и Пуазейля. Движение вязкой жидкости, в том числе и ламинарное, описывается уравнениями НавьеСтокса (1.56)

(1.147)

которые замыкаются уравнением неразрывности

(1.148)

и характеристическим уравнением .

Для установившегося движения несжимаемой однородной жидкости в цилиндрической трубе уравнения упростятся, т. к.  установившееся движение;  несжимаемая жидкость;  осесимметричное течение;  = const  однородная жидкость.

Для условий поля сил земного тяготения X = Y = 0, Z = g. Уравнения Навье-Стокса примут вид

;

; (1.149)

,

а уравнение неразрывности

(1.150)

Анализируя (1.150) можно придти к выводу, что скорость в продольном направлении не изменяется.

Второе уравнение (1.149) означает, что в направлении горизонтальной оси изменение давления равно нулю, иначе говоря, давление в горизонтальных плоскостях постоянно.

Третье уравнение (1.149) выражает закон распределения давления в вертикальных плоскостях. Вследствие малого диаметра труб, применяемых на практике, изменение давления по сечению трубы будет незначительным, поле давления в нем можно считать однородным, а третьим уравнением можно пренебречь. Тогда уравнение движения вязкой несжимаемой однородной жидкости в цилиндрической трубе

. (1.151)

Поскольку правая часть (1.151) является функцией только y и z, а левая  только x, то ввиду независимости координат друг от друга существование его возможно в том случае, когда каждая ее часть представляет собой постоянную величину (метод разделения переменных).

Заменяя частную производную полным дифференциалом и обозначая через падение давления на участке трубы длиной l, получим

const. (1.152)

Знак «» означает уменьшение давления в направлении оси x. Величина представляет собой потери давления на единицу длины, идущие на преодоление сил трения при движении жидкости.

Р

Рис. 1.39. Ламинарное движение жидкости в трубе

ассмотрим некоторое кольцевое сечение на расстоянии r от оси трубы при ламинарном режиме движения жидкости в трубе (Рис. 1.39).

Так как y = z = r , то с учетом (1.152) уравнение (1.149) принимает вид

, (1.153)

но u_x зависит только от r, следовательно уравнение можно записать через полный дифференциал

. (1.154)

Повторно интегрируем (1.154):

,

. (1.155)

Найдем постоянные интегрирования в (1.155): при r = 0 (на оси трубы) , следовательно, c₁ = 0; при r = R (на стенке трубы) u_x = 0, т. к. вблизи стенки существует прилипший слой жидкости (условие прилипания). Тогда из (1.155)

, а .

Следовательно,

.

Окончательно имеем

. (1.156)

На оси трубы скорость

, (1.157)

имеет максимальное значение и с учетом (1.157)

. (1.158)

Уравнение (1.158) выражает собой закон параболического распределения скоростей по сечению трубы (закон Стокса). Линии равных скоростей (изотахи) будут представлять собой концентрические окружности, а их совокупность образует поверхность параболоида вращения.

Среднюю скорость определим из уравнения расхода

.

Элементарную площадку выберем в форме кольца радиусом r и толщиной dr (см. Рис. 1.39), в пределах которого скорость одна и та же и определяется по

.

Площадь кольца = (с точностью до малых второго порядка).

Полный расход через площадь поперечного сечения трубы

.

Итак,

, (1.159)

или, выражая радиус трубы через ее диаметр из (1.159), получаем уравнение Хагена-Пуазейля

. (1.160)

Площадь поперечного сечения трубы , или, выражая радиус трубы через ее диаметр , .

Тогда , или . (1.161)

Сравнивая выражения для средней и максимальной скоростей, можно сделать вывод, что средняя скорость равна половине максимальной

. (1.162)

Гидравлическое сопротивление при ламинарном движении. Запишем уравнение Бернулли для двух сечений трубопровода

.

Если трубопровод горизонтален и одного сечения, то z₁ = z₂ и , а

. (1.163)

Выразим из (1.163) перепад давлений , и поставим его значение в формулу (1.160):

. (1.164)

Расход жидкости в трубе при ламинарном режиме движения может быть определен также по уравнению (1.26):

.

Приравняем правые части уравнений (1.164) и (1.26):

,

откуда

. (1.165)

Умножим и разделим (1.1) на , тогда

или . (1.166)

Обозначая через  коэффициент гидравлического трения в трубах, получим формулу Дарси-Вейсбаха

. (1.167)

При расчете потерь энергии по длине трубопровода некруглого сечения в формулу (1.167) подставляют эквивалентный диаметр, рассчитанный по формуле (1.30), а определяют как функцию от числа Рейнольдса, подсчитанного по эквивалентному диаметру , причем

, (1.168)

где B  коэффициент формы, постоянный для данной формы живого сечения: квадрат  57, равносторонний треугольник  53, кольцо  96.

Зависимость (1.167) называют формулой Пуазейля.

Касательные напряжения при ламинарном движении. Согласно закону Ньютона (1.10)

.

Подставляя в (1.10) значение u_x, получим

.

П

Рис. 1.40. Распределение касательных напряжений по сечению трубы

ри r = 0 (на оси трубы), = 0; при r = R (на стенке трубы), .

Тогда , откуда для ламинарного режима движения имеем линейное распределение касательных напряжений по сечению трубы (Рис. 1.40).

Касательное напряжение на стенке

или . (1.169)

Отношение касательного напряжения на стенке к плотности имеет размерность квадрата скорости и носит название динамической скорости или скорости касательного напряжения на стенке и обозначается

. (1.170)

Согласно (1.126)  гидравлический уклон.

Из (1.169)

. (1.171)

Преобразуем формулу Дарси-Вейсбаха к виду ; так как , то , или с учетом (1.178) , откуда

. (1.172)

Из (1.28) следует и . (1.173)

Основные характеристики турбулентного движения. Подавляющее число движений, встречающихся в технике – турбулентное. Хаотичность турбулентного движения с кинематической точки зрения означает, что скорости жидкости в отдельных точках пространства, через которые она протекает, непрерывно изменяется по величине и направлению.

Скорость u в данной точке турбулентного потока, измеренную в данный момент времени, называют мгновенной. Мгновенная скорость с течением времени изменяется (Рис. 1.41).

Рис. 1.41. Характер изменения

мгновенной скорости

Осредненной называют среднюю за некоторый промежуток времени скорость в данной точке:

, (1.174)

где  промежуток времени, для которого производится осреднение.

Понятие осредненной скорости впервые было предложено Буссинеском (1868 г.) и развито Рейнольдсом. С помощью этого понятия действительный турбулентный поток с его беспорядочно движущимися массами жидкости заменяют воображаемой моделью потока, представляющей совокупность элементарных струек. Их скорости по величине и направлению равны осредненным скоростям.

Отклонение мгновенной скорости от ее осредненного значения,

, (1.175)

называют пульсационной скоростью или пульсацией. Для установившегося движения пульсации изменяют свою величину и знак так, что эффект их осреднения во времени равняется нулю

. (1.176)

Для , промежуток времени осреднения должен быть достаточно большим. Учитывая, что флуктуация скорости в турбулентном потоке происходит с большой частотой, промежуток времени, необходимый для ее осреднения, составляет несколько секунд.

Турбулентные касательные напряжения и механизм их возникновения.

Рис. 1.42. Механизм возникновения турбулентных касательных напряжений

Выделим элементарный слой жидкости, движущейся в направлении оси x с осредненной скоростью (Рис. 1.42). За время dt (меньшее периода осреднения) в силу наличия пульсационной составляющей скорости в поперечном направлении через площадку пройдет элементарная масса жидкости .

Для определения количества движения этой массы жидкости в направлении оси x ее нужно умножить на пульсационную составляющую скорости в направлении x  . Следовательно, количество движения равно .

Внедряясь в близлежащий слой (на Рис. 1.42 он показан пунктиром), элементарная масса теряет свое количество движения, вследствие чего возникает импульс силы .

Сила имеет одинаковое направление со слоем и стремится подтянуть (подравнять по скорости) площадку, лежащую вблизи и обозначенную штриховой линией, к площадке . Однако в соответствии с законом Ньютона возникает сила сопротивления , тормозящая движение этой площадки,

. (1.177)

Поделив обе части уравнения (1.177) на , получим выражение для касательного напряжения .

Итак, касательные напряжения в турбулентном потоке обусловливаются пульсациями или обменом количества движения между соседними слоями жидкости. Слой, движущийся с большей скоростью, подтягивает за собой отстающий и наоборот слой, который движется медленнее, тормозит опережающий. Знак «минус» показывает, что сила сопротивления имеет направление, противоположное продольной пульсации.

Осредненные касательные напряжения

, (1.178)

причем в (1.178) осредненное значение произведения пульсаций не равно нулю.

В схематизированном турбулентном потоке, кроме указанных сил турбулентного обмена вследствие пульсаций, еще проявляются (главным образом вблизи стенки) силы внутреннего трения или вязкости, определяемые по формуле (1.10). Полное касательное напряжение от турбулентных пульсаций и сил вязкости

=+=+. (1.179)

Коэффициент турбулентного переноса. В 1867 г. Буссинеск предложил турбулентное касательное напряжение изображать внешне похожим на закон вязкостного трения Ньютона (1.10)

, (1.180)

где

, (1.181)

называют коэффициентом турбулентной вязкости, или коэффициентом турбулентного переноса. В отличие от коэффициента динамической вязкости в формуле (1.10) коэффициент учитывает не молекулярную структуру жидкости, а особенности турбулентного движения. Он зависит от расстояния до твердой стенки. С приближением к твердой стенке турбулентность затухает, и уменьшается.

Измеряя осредненные скорости и пульсации потока, можно с помощью выражения (1.181) определить коэффициент в данной точке. В некоторых точках потока в сотни и даже тысячи раз больше . Выражение для полного касательного напряжения в турбулентном потоке (1.186) может быть записано как

. (1.182)

Масштаб турбулентности и диссипация энергии. Формулы (1.178) и (1.182) не раскрывают физического содержания явления, поскольку диссипация (рассеяние) энергии происходит не вследствие фиктивной турбулентной вязкости , а в результате действия молекулярной вязкости при беспорядочном движении отдельных частиц жидкости.

По А.Н. Колмогорову механизм диссипации следующий. В турбулентном потоке существуют пульсации разных масштабов. Под масштабом пульсаций (турбулентности) понимают порядок величины расстояний, пройденных «жидкими комками» при их беспорядочном движении в турбулентном потоке как единое целое (с сохранением их индивидуальности). Наибольший масштаб турбулентности определяется размерами установки. Крупномасштабные пульсации переходят в пульсации меньшего масштаба практически без рассеивания энергии, пока они не станут достаточно малыми. Так возникает своеобразный «каскадный» процесс, при котором энергия осредненного движения последовательно передается все меньшим пульсациям, вплоть до движений минимального масштаба, где превалирует влияние вязкости.