
Лекції з курсу фізики «Механіка та молекулярна фізика»
.pdf
Відповідними називають стани різних речовин, які мають однакові значення зведених параметрів. Якщо для різних речовин збігаються значення двох зведених параметрів, то обов’язково співпаде і значення третього параметра.
2.3.8. Ефект Джоуля– Томсона для газу Ван-дер-Ваальса
Процес Джоуля– Томсона полягає в стаціонарному перетіканні газу з камери, де газ має сталий високий тиск P1, до камери, де газ має сталий низький тиск P2, за умови адіабатичної ізоляції як камер, так і з’єднувального газопроводу.
У дослідах Джоуля– Томсона брали циліндричну трубку Т, яку було оточено адіабатною оболонкою А (теплоізолюючим матеріалом). Всередині трубки містився пористий переділ ПП з щільної вати. Поршень П1 створював сталий тиск P1, внаслідок чого газ з камери об’ємом V1 перетікав до камери об’ємом V2 , де він перебував під сталим тиском P2, що його створював поршень П2. Обидва поршні було також теплоізольовано.
При протіканні газу зберігається величина ентальпії I. Покажемо це. Оскільки процес є адіабатичним, то Q=0. Оскільки внутрішня енергія є функцією стану, то її зміна U=U2−U1. У камері, де газ має сталий низький тиск P2, при розширенні від V=0 до V=V2 газ виконує роботу P2(V2− 0)= P2V2. У камері, де газ має сталий високий тиск P1, при стисканні від V=V1 до V=0 газ виконує від’ємну роботу P1(0−V1)= −P1V1. За першим законом термодинаміки Q= U+ A, звідки маємо 0= U2−U1 + P2V2 −P1V1 , тобто U2 + P2V2= U1 + P1V1 , що якраз і означає незмінність ентальпії в процесі Джоуля– Томсона, I1=I2 .
Для ідеального газу I=U+PV=ν CVT+νRT=νCPT. Тому для ідеальних газів незмінність ентальпії в процесі Джоуля– Томсона, I1=I2, є рівнозначною до незмінності температури: T1=T2. А для реальних газів це не так: їхня внутрішня енергія залежить не лише від температури газів, але й від їхніх об’ємів, тому їхня
температура змінюється: T1 ¹ T2 . Зміну температури реального газу в процесі Джоуля– Томсона називають ефектом Джоуля– Томсона.
В термодинаміці розрізняють диференціальний ефект Джоуля– Томсона, коли реальний газ стаціонарним чином протікає крізь пробку, бо зміна тиску при цьому є дуже малою величиною. Відповідно зміна температури при цьому також є малою величиною. Ефект Джоуля– Томсона називають інтегральним, коли зміна тиску є великою, наприклад, P ~10÷100 атм. При цьому газ перетікає крізь маленький отвір, який називається дроселем, і процес перетікання є турбулентним, нерівноважним, але ентальпія при цьому все одно зберігається, бо кінцевий та початковий стани газу є рівноважними. Інтегральний ефект Джоуля– Томсона використовують для отримання зріджених газів.
Розглянемо диференціальний ефект Джоуля– Томсона. Різницю тисків P= P2−P1 вважаємо відомою з експериментальних умов. За відомою різницею P порахуємо зміну температури T
∂T |
|
||
реального газу в моделі Ван-дер-Ваальса, T= ¶P |
|
I |
P. Оскільки в |
|
|
||
процесі Джоуля– Томсона газ перетікає з області високого тиску до області малого тиску, то P < 0 . Знак зміни температури
визначається знаком похідної (¶T / ¶P) I . Коли ця похідна є
позитивною (в цьому разі ефект Джоуля– Томсона називають позитивним), газ в процесі Джоуля– Томсона охолоджується, T<0. І навпаки, коли ця похідна є негативною (в цьому випадку ефект Джоуля– Томсона називають негативним), газ нагрівається, T>0.
Для обчислення похідної (¶T / ¶P) I слід установити зв’язок
між тиском P і температурою T в процесі Джоуля– Томсона. Тому розглянемо спочатку ентальпію (яка є незмінною в цьому процесі) як функцію цих змінних, I=I(P,T). Диференціал ентальпії в процесі
Джоуля– Томсона дорівнює нулю, |
dI = |
∂I |
|
T dP + |
∂I |
|
|
P dT =0. |
|
|
|
||||||||
¶P |
¶T |
||||||||
Звідси знаходимо частинну похідну: |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
∂T |
|
¶I |
|
|
¶I |
|
|
|||
|
|
|
||||||||
|
|
= - |
|
|
T |
|
|
|
P . |
(2.3.54) |
|
|
|
|
|||||||
¶P |
I |
|
¶P |
|
|
¶T |
|
|
||
Диференціал ентальпії у власних змінних було отримано в підрозділі 2.3.4: dI=TdS+VdP. Звідси дістаємо першу з частинних
200 |
201 |

похідних, що входять до виразу (2.3.54): |
∂I |
|
|
|
T |
= T |
∂S |
|
|
T |
+ V . Для |
|||
|
|
|
|
|||||||||||
∂P |
|
∂P |
|
|||||||||||
обчислення похідної ∂S / ∂P |
|
|
|
|
|
|
|
|||||||
T скористаємося співвідношенням |
||||||||||||||
Максвелла (2.3.30). Іншу частинну похідну, |
∂I / ∂T |
|
|
P , яка входить |
||||||||||
|
||||||||||||||
до (2.3.52), було пораховано в підрозділі 2.3.4: ∂I / ∂T P = ν C p .
Це дозволить визначити (∂T / ∂P) |
|
I в такому вигляді: |
|
|||||||||
|
|
|||||||||||
|
|
|
∂T |
|
|
= |
T (∂V |
∂T )P −V |
|
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
I |
|
|
|
|
. |
(2.3.55) |
|
|
|
|
|
|
||||||||
Похідну ∂V / ∂T |
|
|
∂P |
|
|
|
|
ν C P |
|
|||
|
|
|
|
|
||||||||
|
p |
для |
|
|
рівняння |
Ван-дер-Ваальса |
прямо |
|||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
порахувати неможливо. Але можна скористатися термодинамічною
тотожністю (2.3.22) |
і переписати |
∂V / ∂T |
p через |
похідні від |
|||||||||
тиску: |
|
|
|
|
|
|
|
|
|
|
|
||
∂V |
|
|
P = − |
∂P |
|
∂V |
|
|
T = |
(− ∂P / ∂T ) |
|
||
∂T |
|
|
|
|
|
V ∂P |
|
|
V |
. (2.3.56) |
|||
|
|
∂T |
(∂P / ∂V ) |
||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
Для газу Ван-дер-Ваальса похідні, які входять до (2.3.56) вже обчислено раніше (див. (2.3.40)). З урахуванням цього формула (2.3.55) набуває вигляду:
|
∂T |
|
T |
∂P |
V + V |
∂P |
|
|
|
|
|
|
bRT |
− |
2a |
|||||||||||||||
|
|
|
|
|
|
|
|
|
T |
|
|
|
(V − b)2 |
|
V 2 |
|
|
|
|
|||||||||||
= |
∂T |
∂V |
= |
|||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
∂P |
|
|
|
|
|
|
|
ν =1 |
|
∂P |
|
. (2.3.57) |
||||||||||||
|
∂P I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
−νCP ∂V |
|
T |
|
|
|
|
|
|
C p ∂V |
|
T |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Теплоємність |
CP |
завжди |
є додатною, |
похідна |
|
|
|
|
∂P / ∂V |
|
T в |
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
знаменнику (2.3.57) завжди є від’ємною, тому знак похідної (∂T / ∂p)I залежить від знака чисельника у виразі (2.3.57). Іншими
словами, яким буде ефект Джоуля– Томсона, залежить від співвідношення сил притягання та відштовхування частинок
реального газу (з точки зору математики це визначається співвідношенням констант Ван-дер-Ваальса).
Нехай газ є розрідженим, тоді: (V − b)2 ≈ V 2 , значить, з
рівняння Ван-дер-Ваальса |
∂P |
≈ − |
RT |
. За цих умов |
∂V |
|
|||
|
V 2 |
|||
співвідношення (2.3.57) можна наближено переписати в такий спосіб:
|
|
|
|
bRT |
− |
2a |
|
|
2a |
− b |
|
|
|
|
|
|
|
|
|
|
|||||
T |
|
I |
|
V 2 |
V 2 |
= |
RT |
|
||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
. |
(2.3.58) |
||
p |
|
− RTC p |
V 2 |
C p |
|
|||||||
|
|
|
|
|
|
|||||||
З (2.3.58) видно, що існує температура інверсії Tінв , при переході
через яку ефект Джоуля– Томсона змінюється. Температурою інверсії називають:
T = |
2a |
. |
(2.3.59) |
інв |
Rb |
|
τ
27
4
6
Крива інверсії Tin
нагрівання
3
T > 0
T < 0 охолодження
0 |
1/ 3 |
1 |
ϕ |
|
|
Рис. 2.3.6. Крива інверсії для ефекту Джоуля– Томсона
202 |
203 |
Якщо температура, за якої відбувається процес Джоуля– Томсона, є низькою, T < Tінв , тоді в процесі Джоуля– Томсона реальні гази охолоджуються. Якщо експеримент відбувається за високих температур, T > Tінв , тоді реальні гази нагріваються.
Якщо b → 0 (температура інверсії є високою), тоді більшість газів (для них кімнатна температура є нижчою за Tінв ) за
нормальних умов охолоджується, що пояснюється виконанням роботи проти сил молекулярного притягання. Якщо a → 0 (температура інверсії є низькою), тоді більшість газів нагрівається, що не є очевидним, бо не випливає з фізичних міркувань.
Цікаво, що такі гази, як водень H2 та гелій He, в процесі Джоуля– Томсона нагріваються, бо для них температура інверсії є значно меншою за кімнатну температуру. У загальному випадку від’ємний ефект Джоуля– Томсона спостерігається при
температурах: T > |
2a |
V − b |
2 |
||
|
|
|
|
. Нагадаємо, що рівняння Ван-дер- |
|
|
|
||||
|
Rb |
V |
|
|
|
Ваальса при V ³ b є не зовсім придатним.
Корисним є графічне зображення кривої інверсії, яку зручно представити аналітично в обезрозмірених змінних (2.3.52). Тоді для
ефекту Джоуля– Томсона τ = 27(1 − 1 /( 3ϕ ))2 / 4 – це є крива
інверсії (див. рис. 2.3.6), вище якої лежить область нагрівання реальних газів, а нижче – область їхнього охолодження.
Питання для самоконтролю до розділу §2.3. Реальні гази
1.Які сили враховує поправка a в рівнянні Ван-дер-Ваальса?
2.Яка розмірність поправки a в рівнянні Ван-дер-Ваальса?
3.Який порядок величини поправки a в рівнянні Ван-дер- Ваальса в системі СІ?
4.Які сили враховує поправка b в рівнянні Ван-дер-Ваальса?
5.Яка розмірність поправки b в рівнянні Ван-дер-Ваальса?
6.Який порядок величини поправки b в рівнянні Ван-дер- Ваальса в системі СІ?
7.В яких фазових координатах побудовано ізотерму Амага?
8.Спираючись на які фізичні міркування, на ізотермі Ван-дер- Ваальса будують той відтинок лінії, що описує процес конденсації та випаровування?
9.Чим відрізняється критична ізотерма Ван-дер-Ваальса від інших ізотерм?
10.В яких змінних прийнято записувати рівняння Ван-дер- Ваальса в зведеній формі?
11.Сформулюйте закон відповідних станів.
12.Чим відрізняється вираз для внутрішньої енергії реального газу від відповідного виразу у випадку ідеального газу?
13.Чим відрізняється вираз для ентропії реального газу від відповідного виразу у випадку ідеального газу?
14.Що спостерігалося в дослідах Джоуля– Томсона?
15.Чим відрізняються дві області на діаграмі T-V, які розділені кривою інверсії процесу Джоуля−Томсона?
§2.4. Вступ до фізичної кінетики
Фізична кінетика вивчає різноманітні явища перенесення в термодинамічних системах. В даному курсі ми обмежимося вивченням тільки явищ стаціонарного перенесення в газових середовищах. До основних термінів, що ними оперує фізична кінетика, належать, передовсім, довжина вільного пробігу, ефективний переріз молекул.
1. Ефективний переріз молекул газу в даному курсі вводиться виключно для моделі розсіяння частинок (для явищ збудження частинок, іонізації чи розпаду їх на складові частини існують свої величини перерізів). Тому газокінетичний переріз розсіяння
дорівнює σ = π d 2 у випадку, якщо молекули є однаковими, або
σ ≡ σ12 = π ( R1 + R2 )2 у випадку, якщо у газовій суміші присутні два типи частинок з радіусами R1 та R2 , відповідно. В ядерній
фізиці добре зарекомендувала себе модель пучка частинок, який розсіюється на нерухомій мішені. Позначимо інтенсивність пучка:
I = nVвід , де n – концентрація частинок, Vвід – відносна швидкість частинки, тоді переріз розсіяння дорівнюватиме:
204 |
205 |

σ = N / I , |
(2.4.1) |
де N – середня кількість частинок, які за одну секунду вибувають з пучка через пружні зіткнення. Для частинок ідеального газу, які взаємодіють між собою виключно внаслідок пружних зіткнень, σ
слабко залежить від Vвід . Врахування сили взаємодії між молекулами газу зроблено в моделі твердих пружних кульок Сезерлендом: σ = σ 0 (1 + const / T ) .
2. Довжина вільного пробігу молекул як термін фізичної кінетики була введена Клаузіусом. Це – середня відстань, яку проходить частинка між двома послідовними зіткненнями. Скористаємося наступною моделлю: частинки газу є твердими кульками, які взаємодіють тільки пружно, тому відбуваються тільки процеси розсіяння. Частинки газу летять зі швидкістю, яка
має порядок величини: VT ( T = 0oC ) =1700; 455 та 425 м/с для водню, азоту та кисню, відповідно. Тоді V = σ VT – це об’єм, що описується перерізом σ в процесі руху частинки газу зі швидкістю VT за 1сек. Обчислимо добуток V × n та отримаємо кількість зіткнень цієї частинки за одну секунду як кількість частинок, що їх зустріла молекула на своєму шляху за 1 сек: z = nV = nσVT . Тоді
шлях, що буде долатися частинками між двома послідовними зіткненнями, дорівнюватиме:
λ = VT / z = 1 /( nσ ) . |
(2.4.2) |
Якщо врахувати розподіл молекул за швидкостями, що зробив Максвелл, тоді вираз для довжини вільного пробігу дещо
зменшиться порівняно з (2.4.2): λ = 1 /( 
 2nσ ) .
2nσ ) .
3. Розподіл за довжиною вільного пробігу обумовлено пружним розсіюванням одних частинок на інших. Виділимо у газі частинки, що летять вздовж осі x . Модельно вважаємо ці частинки “ пучком”. Нехай в х=0 маємо інтенсивність пучка, який утворюють ці частинки, І0. Рухаючись у пучку, частинки зазнають пружного розсіювання на інших частинках, внаслідок чого інтенсивність пучка зменшується. Знайдемо значення інтенсивності як функцію координати: I(х). Для цього розглянемо шар газу площею S,
товщиною dx від координати x = 0 до відстані d x . Кількість
частинок газу у цьому прошарку дорівнює: n S dx. Середня кількість частинок пучка, які розсіюються на “ мішені” ( тобто на
якійсь одній |
частинці |
з тих, що не |
рухаються |
вздовж |
осі |
x , |
перебуваючи |
в об’ємі |
S dx) за одну секунду, |
дорівнює |
Iσ . |
||
Кількість “ мішеней” |
визначається |
добутком: |
n S dx, |
значить, |
||
кількість розсіяних за одну |
секунду в об’ємі S dx частинок пучка |
||||||||
дорівнює за абсолютною |
величиною: |
|
dN |
|
= |
|
Iσ S n dx |
|
. Але |
|
|
|
|
||||||
диференціал кількості цих частинок є від’ємним, бо внаслідок розсіяння частинки вибувають з пучка, тому поставимо знак «мінус» та введемо позначення λ≡1/(nσ). Це дозволить переписати вираз для розсіяних частинок в такий спосіб: dN = −ISdx / λ . Отже, dN = −Ndx / λ , тобто імовірність dN/N частинці вибути з пучка внаслідок пружного зіткнення на відрізку [x, x+dx] є пропорційною до dx, а множник 1/λ відіграє роль густини імовірності. Проінтегрувавши диференціальний вираз для імовірності вибування частинки з пучка при пружному розсіюванні,
можна |
знайти |
розподіл |
частинок |
вздовж |
осі |
x : |
N = N( x = 0 )exp( −x / λ ) . Це, |
в свою чергу, дає |
можливість |
||||
визначити інтенсивність “ пучка” |
частинок газу: |
|
|
|||
|
|
I = I0 exp( −x / λ ) . |
|
|
(2.4.3) |
|
Наявність знака «мінус» у (2.4.3) вказує на те, що відбувається зменшення частинок пучка в процесі їхнього льоту.
Класичний експеримент, що його провели Борн та Борман, підтверджує цю теорію. Дослідна установка складалася з камери, в якій вздовж спільної осі було розташовано послідовно, один за одним, чотири диски з круглими отворами по центру. Тиск повітря в камері контролювався насосами, диски охолоджувалися рідким азотом. На кожному диску було закріплено скляний квадрант, що був повернутий відносно попереднього на π/2. В результаті експериментів з’ясували, що відносна кількість атомів срібла, які
осіли на два перші квадранти з координатами |
х1,2, дорівнює: |
|
N1 N2 = exp[( x2 − x1 ) / λ ]. Змінюючи тиск в |
камері, |
було |
отримано дані, які дозволили дійти висновку: |
λ P−1. |
Це |
підтверджує теоретичний результат (2.4.2). |
|
|
206 |
207 |

2.4.1. Дифузія у газах
Дифузією називають процес перенесення речовини. Він виникає, коли порушено умови хімічної рівноваги. Розрізняють взаємну дифузію та самодифузію. Якщо камеру поділено на дві частини, в яких знаходяться гази 1 та 2, то після усунення заслінки між частинами камери ці гази через броунівський рух перемішаються, а їхні концентрації в усьому об’ємі вирівняються. Це випадок взаємної дифузії. Якщо заслінка ділить камери так, що однаковий газ різної концентрації займає дві її частини, то прибравши заслінку, отримаємо можливість спостерігати явище самодифузії газу. Експериментально самодифузію досліджують так: або змішують радіоактивні ізотопи з неактивними, або беруть різні хімічні гази (нехай це буде СО та N2), які мають однакові маси та майже однакові за розмірами молекули. І проводять дослідження з такими газами.
Для отримання рівняння, яке кількісно описує явище дифузії, слід ввести термін, який кількісно описує цей процес: густину дифузійного потоку. Під цим терміном будемо розуміти кількість молекул досліджуваного газу, які проходять крізь переріз з одиничною площею, що орієнтована перпендикулярно до градієнта концентрації, за одиницю часу. В теорії задачу дифузії зводять до знаходження густини цього потоку.
Молекулярно-кінетична теорія коефіцієнта дифузії ідеального газу полягає, головне, в наступному. Нагадаємо, що інтенсивність пучка концентрацією n, який рухається із швидкістю V, дорівнює: I=nV. Оскільки фізичним механізмом дифузії є хаотичний тепловий рух молекул газу, за характерну швидкість обираємо теплову швидкість молекул VT . Молекули рухаються в усіх напрямках з однаковою імовірністю, але ми модельно поділимо їх на шість (!) потоків, вважаючи, що в кожній точці тривимірного простору є шість потоків, з яких тільки один рухається в потрібному (наприклад, + x ) напрямку. Тоді густина кожного з цих шести потоків ушестеро менша за густину газу в цілому, і кількість частинок N, що за одиницю часу перетинають площу S в напрямку
нормалі до неї, дорівнює: N = nVT S / 6 . Кількість частинок, які
при цьому русі розсіюються в прошарку елементарної довжини dx, описується виразом (2.4.3). Його диференціал дорівнює:
|
dN = |
− N( x ) |
− x |
λ dx = |
− nV S |
e |
− x |
λ dx. |
(2.4.4) |
||||||
|
|
λ |
e |
|
T |
|
|||||||||
|
|
|
|
|
|
|
|
|
6λ |
|
|
|
|
||
Кількість частинок, які переносяться за одну секунду через |
|||||||||||||||
переріз S в напрямку |
|
+ x , |
дорівнює сумі всіх потоків, які |
||||||||||||
стартували до перерізу S з різної відстані до |
нього: |
Γ+ = ∫ dN . |
|||||||||||||
Розклавши у виразі для dN |
концентрацію n(x) в ряд Тейлора: |
||||||||||||||
n(x)= n( 0 ) + x |
dn |
|
|
x=0 , |
з точністю до лінійних доданків за малим |
||||||||||
|
|
||||||||||||||
dx |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
відхиленням x, знайдемо дифузійний потік в цьому напрямку ( + x ):
|
Γ+ |
= |
V S |
|
+∞ |
+ x |
dn |
|
|
|
|
|
|
|
|
− x |
λ ) |
|
||||||||||||||||||||||||
|
|
|
|
T |
|
∫ [ n( 0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
]d( e |
|
||||||||||||||||||||||
|
|
|
|
6 |
|
dx |
|
x=0 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
V S |
|
|
|
|
V S +∞ |
− x |
|
λ |
dn |
|
|
||||||||||||||||||||||||||||
|
|
= |
|
T |
|
n( 0 )S − |
T |
|
|
|
∫ |
e |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|||||||||||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
6 |
|
6 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
x=0 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
= |
VT S |
n( 0 )S − |
VT |
S |
dn |
|
|
|
|
|
λ . |
|
(2.4.5) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
− 6 |
|
|
|
|
|
|
|
6 |
|
|
dx |
|
|
|
x=0 |
|
Γ− в |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
В аналогічний |
|
|
спосіб знайдемо |
|
|
|
дифузійний |
потік |
||||||||||||||||||||||||||||||||||
протилежному напрямку ( − x ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
nV S |
+ x |
|
|
|
V S |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dn |
x |
|
|||||||||||||||
Γ− = |
∫ |
|
T |
|
|
|
e |
λ dx = |
T |
|
|
∫ |
[ n( 0 ) + x |
|
|
|
|
]d( e |
λ ) |
|||||||||||||||||||||||
6 |
λ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
−∞ |
|
|
|
|
|
6 |
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
x =0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
VT S |
[ n( 0 ) − |
dn |
|
|
|
|
λ ]. |
|
(2.4.6) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
dx |
|
x =0 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Повний дифузійний потік складається з цих двох (Γ+ та Γ– ) потоків, що поширюються у протилежних напрямках:
Γдиф = Γ+ + Γ− = |
VT λS |
|
dn |
|
. |
(2.4.7) |
|
− 3 dx |
|||||||
|
|
x=0 |
|
||||
208 |
209 |

Введемо коефіцієнт дифузії ідеального газу: D = VT λ / 3 . Тоді вираз
для стаціонарного дифузійного потоку можна переписати в наступний спосіб:
Γ = −DS |
dn |
. |
(2.4.8) |
диф
dx x=0
Закон, який визначає залежність величини дифузійного потоку від градієнта концентрації частинок газу, називається першим законом Фіка: Γдиф grad( n ). Попри те, що ми здобули вираз (2.4.8)
теоретично для моделі ідеального газу, закон Фіка було встановлено експериментально, він є справедливим для більшості речовин. Таким чином, необхідною умовою виникнення явища дифузії є наявність градієнта концентрації частинок. Внаслідок дифузії виникає потік речовини в напрямку, що є протилежним до градієнта концентрації.
Коефіцієнт дифузії пов’язано з рухливістю частинок газу. У випадку, коли газ знаходиться у зовнішньому стаціонарному потенціальному полі, на хаотичний рух частинок накладається їхній
регулярний рух у напрямку сили |
r |
|
|
|
F . У випадку досить слабкої сили |
||||
швидкість в лінійний спосіб залежить від сили: |
r |
r |
це |
|
u |
= BF , тут В – |
|||
рухливість частинок. У стаціонарному стані частинки газу під дією цієї сили розташовуються у просторі так, що для їхньої концентрації реалізується розподіл Больцмана за потенціальною
енергією: n = n0 exp( − E p 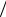 kT ), де потенціальна енергія E p = −Fx
kT ), де потенціальна енергія E p = −Fx
(детально про розподіл Больцмана йтиметься у підрозділі 2.5.10). Тоді у стані рівноваги дифузійний потік (2.4.8) дорівнює силовому
потоку: ΓF = unS . |
Наприклад, у випадку гравітаційного поля |
E p = −m0 gx , де m0 |
– це маса частинки газу, градієнт концентрації |
обчислюється досить просто. Тоді з рівності потоків Γдиф = ΓF для
коефіцієнта дифузії маємо співвідношення Ейнштейна– Смолуховського:
D = BkT . |
(2.4.9) |
Воно пов’язує рухливість B (молекулярний параметр) з коефіцієнтом дифузії D та температурою T (це − макропараметри).
2.4.2. Термодифузія
Явища дифузії не обмежуються розглянутою вище дифузією. Наповнимо камеру однорідною сумішшю двох різних газів з масами молекул m j та радіусами R j . Якщо протилежні стінки
камери тримати при різних температурах Т1 та Т2, тоді в системі виникає явище термодифузії. Воно полягає в тому, що в цьому випадку масивні частинки прямують до холодної стінки, а легкі –
до гарячої. Якщо m1 ≈ m2 , тоді великі частинки, наприклад, з
радіусом R2 (R2 >R1), прямують до холодної стінки, а дрібні – до гарячої. Напрямок термодифузійного потоку залежить від сили взаємодії між частинками. Теорію термодифузії розроблено для моделі твердих кульок, які відштовхуються за певним законом. Потік частинок типу 1, що за одиницю часу перетинають контур з одиничною площею, складається з термодифузійного та дифузійного потоків. Його аналітичний вираз має вигляд:
Γ |
|
= n |
DT |
|
dT |
− nD |
dC1 |
, |
|
(2.4.10) |
|
|
T |
|
|
|
|||||||
|
1 |
|
|
dx |
12 |
dx |
|
|
|||
тут DT – термодифузійний |
коефіцієнт, |
n=n1+n2 – |
це сумарна |
||||||||
концентрація частинок, С1 = n1 / n – |
відносна |
концентрація |
|||||||||
частинок першого типу.
В стаціонарному стані (камеру закрито) величина потоку дорівнює нулю: Γ1 = 0 . Значить, (DT /T)dT/dx=D12 dC1 /dx, звідки для відносної концентрації маємо наступний аналітичний вираз:
C1 ( T ) = C1( T1 ) + kT lnT / T1 , |
(2.4.11) |
де kT = DT / D12 const . Це явище можна використати для
розділення речовин.
Існує метод Клаузіуса– Дікеля для розділення ізотопів, який використовує явище термодифузії. Пристрій в цьому методі складається з дуже довгої, але тонкої труби (h~10м, d~1см), вздовж осі якої протягнуто металевий дріт з температурою, що перевищує тисячу градусів за Цельсієм. Тоді внаслідок термодифузії поблизу зовнішньої холодної стінки збираються важкі ізотопи, а біля гарячого дроту – легкі ізотопи однієї речовини.
210 |
211 |
2.4.3. Другий закон Фіка (нестаціонарна дифузія)
Побіжно ознайомимося з одновимірною задачею про зміну концентрації компонентів n j ( x,t ) суміші газів з часом внаслідок
дифузії. Це буде корисним також для отримання навичок здобуття диференціальних рівнянь у частинних похідних. Нехай для спрощення
математичних |
викладок |
суміш складається з двох газів: |
n1 + n2 = n0 = const , усі |
частинки характеризуються однаковою |
|
температурою: |
T = const , |
на суміш не діють зовнішні сили: F = 0 . |
Здобудемо рівняння, яке описує зміну концентрації n j ( x,t ) з часом.
Розглянемо частинки j-го ґатунку, які містяться в елементарному об’ємі з поперечним перерізом S товщиною x. Кількість частинок j-го ґатунку, які за час dt внаслідок самодифузії влетять до зазначеного об’єму крізь контур S з координатою x, який є
перпендикулярним до осі x , |
дорівнює dN j ( x,t ) = −D |
∂n j |
|
Sdt . |
||||||||
∂x |
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Крізь такий самий контур S з координатою x+ |
x досліджуваний об’єм |
|||||||||||
S × x за час dt полишать dN j ( x + |
x,t ) = −D |
∂n j |
|
Sdt |
частинок. |
|||||||
∂x |
|
x + x |
||||||||||
Різниця між кількістю dN j ( x + |
x ) |
|
|
|
|
|
|
|
|
|||
частинок, які полишають об’єм |
||||||||||||
S × x , та кількістю dN j ( x ) частинок, які надходять до цього об’єму,
обумовлює зміну в часі кількості частинок j-го ґатунку, що знаходяться у зазначеному об’ємі:
N= dN j ( x,t ) − dN j ( x + |
x,t ) = − D |
∂n j |
Sdt + D |
∂n j |
|
Sdt |
|||||||||||||
∂x |
|
x |
∂x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + x |
||||
|
dn j |
|
dn j |
|
|
|
|
|
|
|
∂ |
∂n j |
|
|
|||||
= Sdt D |
|
|
|
− D |
|
|
|
|
= Sdt |
|
D |
|
|
|
|
x . (2.4.12) |
|||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
dx |
|
x + x |
|
|
|
x |
|
|
|
|
∂x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Коли поділити зміну кількості частинок |
|
N на об’єм S |
x , в якому ця |
||||||||||||||||
зміна відбулась, ми здобудемо зміну концентрації в обраній точці
212
|
∂ |
|
∂n j |
|
|
простору з часом: n(x,t)= N/(S x)= dt |
|
|
|
|
В такий спосіб |
|
|
||||
|
D |
∂x |
. |
||
|
∂x |
|
|
||
ми здобули рівняння нестаціонарної дифузії:
∂n j (x,t ) |
|
∂ |
|
∂n j |
|
||
|
|
= + |
|
D |
|
. |
(2.4.13) |
|
|
|
|
||||
∂t |
|
|
|
∂x |
|
|
|
|
∂x |
|
|
||||
При цьому, якщо має місце рівність: n0 D = const( x ) , тобто коли
коефіцієнт дифузії не залежить від координати, тоді (2.4.13) можна переписати у більш зручному для наступного аналізу вигляді:
1 |
|
∂n j |
|
1 |
|
∂ |
n D ∂n j |
|
∂ |
|
1 |
|
∂n j |
|
|||||
|
|
|
= |
|
|
|
|
0 |
|
|
|
= D |
|
|
|
|
|
. |
(2.4.14) |
n ∂t |
n |
|
|
n |
|
∂x |
|
|
|
∂x |
|||||||||
|
|
∂x |
|
|
|
∂x n |
|
|
|
||||||||||
0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
Рівняння (2.4.14) є подібним до того, яке описує явище нестаціонарної теплопровідності. З (2.4.14) видно, що з часом величина відносної концентрації C j = n j / n0 може або зростати, або зменшуватися в
залежності від форми кривої: C j = C j ( x ) . Це прямо витікає з рівняння для відносної концентрації:
∂С |
j |
(x,t ) |
= D |
∂2С |
j |
. |
(2.4.15) |
||
|
∂t |
|
∂x |
2 |
|
||||
|
|
|
|
|
|||||
Отже, концентрація частинок j-го ґатунку зростає з часом, якщо C j = C j ( x ) описується угнутою кривою (бо саме для такої кривої лінії має місце додатність другої похідної). А якщо ж графічна залежність C j = C j ( x ) є опуклою, тоді величина C j з часом
зменшується. Рівняння (2.4.15) є прикладом параболічних диференціальних рівнянь у частинних похідних, які вивчаються у курсі математичної фізики.
213
2.4.4. Теплопровідність газів
Теплопровідність, разом із конвекцією та випромінюванням тепла, є одним із способів передачі теплової енергії. Всі ці нерівноважні процеси виникають внаслідок порушення умов теплової рівноваги, тобто наявності у термодинамічній системі градієнтів температури.
Кількісною характеристикою теплопровідності є тепловий потік Q, тобто кількість теплоти, яка переноситься внаслідок хаотичного теплового руху крізь контур S, що орієнтовано перпендикулярно до градієнта температури, за одиницю часу. Тепловий потік вимірюється в Дж/сек=Вт. Густиною теплового потоку q = dQ/dS називають тепловий потік, що тече крізь контур одиничної площі. За розмірністю [q]= Вт/см2.
Порахуємо тепловий потік в наступному випадку. Нехай температура ідеального газу змінюється вздовж осі x . Розташуємо контур площею S поперек осі x в місці з координатою x = x0 .
Молекулярно-кінетична теорія коефіцієнта теплопровідності ідеального газу полягає в наступному. Ґрунтуючись на тих самих міркуваннях, що і у підрозділі 2.4.1, вважаємо, що кількість частинок N, які за одиницю часу перетинають контур площею S зліва праворуч, дорівнює: N = nSVT / 6 . Кожна з молекул газу в середньому
переносить енергію ε, яку за теоремою про рівномірний розподіл енергії можна порахувати в такий спосіб: ε =ikT/2, де i – це кількість ступенів вільності. Таким чином, кількість теплової енергії, що її переносять молекули ідеального газу крізь контур в зазначеному напрямку за час dt, дорівнює:
Q |
= |
nVT |
Sdt × |
ikT |
. |
(2.4.16) |
|
|
|||||
+ |
6 |
2 |
|
|
||
|
|
|
||||
Оскільки температура газу залежить від координати x, виникає питання, яку саме температуру слід використовувати у формулі (2.4.15). Для відповіді на це питання скористаємося наступними міркуваннями.
Молекули, які перетинають контур, характеризуються температурою того місця, в якому вони востаннє провзаємодіяли з
214
молекулами фонового газу, тобто вони несуть температуру того газу, з яким востаннє зіткнулися. Як відомо, відстань, яку в середньому молекули проходять без зіткнень, називають довжиною вільного пробігу λ. Отже, температуру T у формулі (2.4.16) слід обчислювати лівіше від точки спостереження на одну довжину вільного пробігу λ, тобто в точці x=x0−λ.
Аналогічно можна записати вираз для кількості тепла, яке переноситься частинками крізь цей перетин ліворуч (проти осі x ). Він є подібним до (2.4.16), лише температуру слід брати у точці x=x0+λ. Це пояснюється тим, що частинки, які рухаються ліворуч крізь перетин S, востаннє зазнали зіткнень праворуч від контуру на відстані, що в середньому дорівнює довжині вільного пробігу. Тобто, зліва праворуч за час dt внаслідок хаотичного теплового руху молекул ідеального газу крізь контур S переноситься:
Q |
= |
nVT |
Sdt × |
ikT( x0 − λ ) |
. |
(2.4.17) |
|
|
|||||
− |
2 |
|
|
|||
|
6 |
|
|
|||
Аналогічно тому, як це було у випадку дифузії, результуючу кількість тепла порахуємо як різницю того, що перенесено праворуч, і того, що перенесено йому назустріч: Q= Q+− Q− . Обчислимо її, розкладаючи величину температури в ряд Тейлора за малою величиною λ в околі точки спостереження x0 :
|
|
|
|
ikVT nS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Q = |
|
|
|
dt[ T (x0 |
- λ ) - T (x0 + λ )] |
|
|
||||||||||||||
|
|
|
12 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ikV |
nS |
|
|
|
|
|
|
dT |
|
|
|
|
|
|
|
|
dT |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= |
T |
|
dt |
T( x ) - λ |
|
|
|
|
|
|
- T( x ) + λ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
12 |
|
|
|
0 |
|
dx |
|
|
|
|
0 |
|
|
dx |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||||
|
|
|
|
|
|
|
|
= |
|
ikλVT n |
Sdt |
|
dT |
|
x . |
|
(2.4.18) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
- 6 |
|
dx |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Визначимо тепловий потік, що переноситься крізь площу S, яку розташовано поперек осі x в точці спостереження x0 :
215
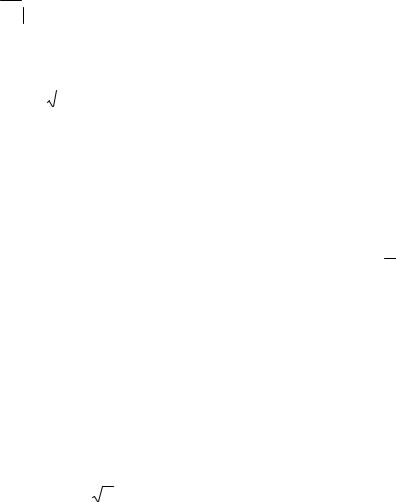
Q=−κ S |
dT |
(2.4.19) |
. |
dx x0
Тут κ – це коефіцієнт теплопровідності, для моделі ідеального газу він дорівнює:
κ = |
iknVT λ |
µ |
|
T |
|
. |
(2.4.20) |
|
|
|
|||||
6 |
|
σ |
|
||||
Якщо скористатися визначенням внутрішньої енергії однієї частинки: U = ikT / 2 , то можна вирахувати питому теплоємність цього газу за
умов теплопередачі |
при |
сталому значенні об’єму: c |
= |
n |
|
dU |
|
|
|
|||||||
|
|
|
|
|||||||||||||
|
|
|||||||||||||||
= |
N |
|
ik |
= |
ik |
, а |
|
V |
|
ρ dT |
|
V |
||||
|
|
|
|
|||||||||||||
|
потім |
переписати коефіцієнт теплопровідності |
||||||||||||||
|
|
|
||||||||||||||
m 2 2m0
ідеального газу (2.4.20) в інший спосіб: κ = VT λcV ρ / 3 .
Експериментально явище теплопровідності вивчав Фур’є, який і вивів закон, що визначає пропорційність теплового потоку до градієнта температури:
Q µ grad( T ) . |
(2.4.21) |
З закону Фур’є (2.4.21) можна зробити висновок, що для реалізації явища теплопровідності в системі має бути неоднорідний профіль температури ( grad T ¹ 0 ) . При цьому тепло переноситься від гарячого місця термодинамічної системи до її холодного, тобто в напрямку, що є протилежним до grad T . Для моделі ідеального газу
коефіцієнт теплопровідності є пропорційним до |
T . |
Тепловий опір. Як відомо, аналогія – |
це потужний метод |
пізнання у фізиці. Скористаємося ним, щоб показати подібність явищ перенесення тепла та електричних зарядів. Нагадаємо, що в електриці потік електричних зарядів – сила струму I, тобто заряд, що за одну секунду протікає крізь перетин S дроту довжиною x з питомою
216
електропровідністю γ під дією різниці потенціалів Δϕ, визначається
1 |
|
x |
||
законом Ома: I= Δϕ /R. Тут електричний опір R= |
|
|
|
. |
γ |
S |
|||
Перепишемо тепловий потік (2.4.19) в такій формі, що є |
||||
аналогічною до закону Ома: |
|
|
|
|
T |
|
1 |
x |
−1 |
|
||
|Q|= κ S |
= |
T × |
|
|
. |
(2.4.22) |
|
κ |
|||||||
x |
|
|
S |
|
|
||
Закон Ома є аналогічним до формули (2.4.22): електричний струм I є аналогічним до теплового потоку Q; різниця потенціалів Δϕ на кінцях дроту є причиною електричного струму, а різниця температур T є причиною теплового потоку. Завершуючи перелік цієї низки аналогій, зазначимо, що електричний опір R є аналогічним до коефіцієнта
RT = 1 x , який природно назвати тепловим опором.
κ S
Коефіцієнт температуропровідності. Цей коефіцієнт виникає в задачах про нестаціонарну теплопровідність, в яких тепловий потік змінюється з часом. Тому розглянемо цю задачу побіжно. Для спрощення задачі, як і в попередніх випадках, розглянемо одновимірний випадок, тобто вважаємо, що температура системи змінюється в одному напрямку, який позначимо x . Виділимо елементарний об’єм перетином S і товщиною dx, чий лівий край визначається координатою x0, а правий – x0+ dx. Порахуємо зміну температури цього об’єму з часом. За час dt до обраного об’єму внаслідок теплопровідності надходить кількість тепла q( x0 )Sdt , а
витікає q( x0 + x )Sdt , тут q – густина потоку тепла. Отже, в об’ємі S∆x за час dt внаслідок теплопровідності кількість тепла змінюється на
таку величину: Q= q( x0 )Sdt − q( x0 + |
x )Sdt = − Sdt[ q( x0 + |
x ) |
− q( x0 ) ] = - Sdt × grad( q ) x . Оскільки |
газ в обраному об’ємі |
не |
виконує жодної роботи, накопичення тепла призводить до зростання внутрішньої енергії, а отже, і температури газу в цьому елементарному об’ємі на величину T = Q/(ρ cV S x) = - dt × grad( q ) /(ρ cV). Тим самим ми знову здобули рівняння нестаціонарної теплопровідності:
217

|
|
∂T |
= − |
|
∂q |
= |
∂ |
|
∂T |
|
|||||
cV ρ |
∂t |
|
|
|
|
|
κ |
|
. |
(2.4.23) |
|||||
∂x0 |
∂x |
||||||||||||||
|
|
|
|
|
|
∂x |
x0 |
|
|||||||
Якщо коефіцієнт |
теплопровідності |
не |
залежить від |
координати, |
|||||||||||
∂κ / ∂x = 0 , тоді рівняння теплопровідності спрощується: |
|
||||||||||||||
|
|
|
|
dT |
= χ |
∂2T |
, |
|
|
(2.4.24) |
|||||
|
|
|
|
|
∂x2 |
|
|
||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
||||
де χ = κ /( ρ CV ) |
– це коефіцієнт температуропровідності, який має |
||||||||||||||
ту саму розмірність, що й коефіцієнт дифузії: [χ ] = м2 / c . Для моделі ідеального газу коефіцієнт температуропровідності залежить від
термодинамічних |
параметрів |
у |
наступний |
спосіб: |
|||||||
|
|
λ |
|
|
|
3 |
|
|
|
|
|
χ = |
V |
= |
V |
|
T 2 |
|
|
|
|
||
T |
|
T |
|
. За своїм фізичним змістом, коефіцієнт χ – |
|||||||
3 |
3nσ |
Pσ |
|||||||||
|
|
|
|
|
|
|
|||||
це швидкість зміни температури в тій точці середовища, в якій залежність T(x) є такою, що ∂ 2T/∂ x2=1.
2.4.5. Внутрішнє тертя
Явище внутрішнього тертя виникає в термодинамічних системах, де є відносний направлений рух однієї макрочастини системи відносно іншої. Розглянемо приклад: нехай між двома паралельними пластинами знаходиться газ. Якщо одну з пластин почати рухати, то виникає сила, яка рухатиме другу пластину. Це є сила внутрішнього тертя. Нехай відстань між пластинами є значно більшою, ніж довжина вільного пробігу. Тоді про пластини можна забути та говорити просто, що в термодинамічній системі є неоднорідний в поперечному напрямку (нехай це буде вісь x )
розподіл повздовжніх швидкостей: u y = u y ( x ) . Якби газ (як ціле) не
рухався, тоді б середнє значення вектора швидкості дорівнювало r
нулю: V = 0 , що обумовлено рівноправністю усіх напрямків руху
218
частинок, які беруть участь у хаотичному броунівському русі. Та, оскільки у середовищі є упорядкований рух, значить, середнє значення вектора швидкості характеризується швидкістю упорядкованого руху:
r |
r |
V |
= u y ( x )ey . Але хаотичний тепловий рух призводить до переходу |
частинок з області швидких частинок (великі значення u y ) до області повільних частинок (малі значення u y ) та навпаки. Тому через
зіткнення між частинками відбувається передача імпульсу у поперечному напрямку x . Швидкі частинки, переходячи до області повільних частинок, прискорюють упорядкований рух частинок цієї області. А повільні частинки, потрапляючи до області швидких частинок, уповільнюють упорядкований рух частинок цієї області. В результаті цього відбувається вирівнювання поздовжньої швидкості упорядкованого руху в системі. Зміна імпульсу направленого руху свідчить про існування в системі сили тертя.
Порахуємо цю силу тертя. Оберемо контур площею S, перпендикулярний до осі x , в точці x=x0. Кількість частинок, які за одиницю часу перетинають цей контур у напрямку ( + x поперек напрямку упорядкованого руху), дорівнює кількості частинок, які перетинають її в протилежному напрямку ( − x поперек напрямку упорядкованого руху). Як вже було показано в підрозділі 2.4.1, присвяченому вивченню дифузії в ідеальному газі, ця кількість дорівнює nVT S / 6 . Молекули, які внаслідок хаотичного теплового
руху перетинають контур у додатному напрямку + x , несуть імпульс m0uy(x0−λ) упорядкованого руху, властивий для того шару газу, в якому ці молекули востаннє зіткнулись. Отже, за одиницю часу в напрямку + x переноситься імпульс Г+= m0uy(x0−λ) nVT S / 6 .
Аналогічно порахуємо імпульс, що його внаслідок хаотичного теплового руху переносять молекули крізь обраний контур у
зворотному напрямку: Г−= m0uy(x0+λ) nVT S / 6 . Оскільки швидкість направленого руху молекул змінюється вздовж осі x , то ці потоки є різними за величиною: Г+ ¹ Г− . Імпульс, що його правий шар газу (той, що лежить правіше обраного контуру x=x0) передав лівому шару (тому, що лежить лівіше обраного контуру x=x0) за одиницю часу, дорівнює силі Fтер, з якою вони взаємодіють:
219
