Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Практика ФКП

.pdf

Скачиваний:

Добавлен:

13.03.2016

Размер:

1.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Вычисление интегралов

f x dx

Пусть

функция

f z

Pk z

есть

отношение двух

многочленов,

где

n k 1 и

Qn z

z1, z2,

,zN есть нули знаменателя Qn z ,лежащиевверхнейполуплоскости.Тогда

f x dx 2 i Res f zk .

(6.9)

k 1

Пример6.12. Вычислитьинтеграл I

x2dx

1 x

0 x

Решение.Так как подынтегральная функция является четной, то

x2dx

1 x

0 x

Функция f z

есть отношение многочлена степени k 2 к много-

z2 1 z2 4

члену степени

n 4, т.е. условие

n k 1 выполняется. Функция

f z

в верхней

полуплоскости имеет две особые точки z i ,

z 2i , поэтому по формуле (6.9)

x2dx

I 1

1 2 i Res

Res

1 z

1 x

z i

z 2i

Дляфункции f z

точки z i, z 2i являют-

z2 1 z2 4

z i z i z 2i z 2i

ся полюсами первого порядка. Поэтому для вычисления вычетов воспользуемся формулой (6.5):

z2 z i

z2 z 2i

I i

Res

lim

1 z

z i

z 2i

z i

i lim

lim

z i

z 2i

2i 3

3 4i

z i z

z 1 z 2i

f x eiax dx,

f x cosaxdx,

f x sinaxdx

Вычисление интегралов

Пусть

функция

f z

Pk z

есть

отношение

двух

многочленов,

где

k n

Qn z

z1, z2,

,zN

естьнулизнаменателя Qn z ,лежащиевверхнейполуплоскости.Тогда

f x eiaxdx

f z eiaz ,

a 0.

(6.10)

2 i

Res

z z

k 1

Отметим, что eiax cosax isinax. Поэтому


		f x eiax dx		f x cosaxdx i		f x sinaxdx .

Следовательно, можно записать


	f x cosaxdx Re		f x eiaxdx ,		f x sinaxdx Im		f x eiaxdx .	(6.11)

и воспользоваться формулой (6.10) и для этих типов интегралов.

	x 1 cosx			dx .
Пример6.13. Вычислитьинтеграл I	x	2	2x 5

Решение.Воспользуемсяпервойизформул(6.11):

x 1 cosx

x 1 eix

2x 5

dx Re

dx .

z 1

2x 5

Функция

f z

есть отношение многочлена степени k 1 к многочле-

z2 2z 5

ну степени n 2,

т.е. условие

k n , необходимое для применения формулы (6.10),

выполняется.

Найдем

нули

знаменателя

z2 2z 5

функции

f z :

это

точки

z1 1 2i,

z2 1 2i ; в верхней полуплоскости находится первая из них. Поэтому

применяя формулу (6.10), получим

x 1 ei x

z 1 eiz

I Re

dx Re 2 iВыч

2z 5

2x 5

z z1 z

Вычет

точке

z z

для

функции

вида

случае,

когда

z 0, z

0, z

можно

вычислить

по

формуле

Выч

z z1

Поэтому

z 1 eiz

I Re

2 iВыч

2 i

2z 2

z z

z z1 z2 2z 5

z z1

i 1 2i

Re i e

2 i

Re i

cos1 isin1

sin1.

Re i e

Примеры для самостоятельного решения

sinx

cosx

Вычислить:

x 1

dx,

dx .

x2 4x 13

x2 1

1 x

Ответы:

2e 1 .

12e

7. Элементы операционного исчисления

7.1. Оригинал и его изображение

Комплекснозначная функция f t u t iv t вещественного аргумента t

называется оригиналом, если она удовлетворяет следующим условиям:

1) функция f t			кусочно-непрерывна;
2)	f t 0 при t		0;
3)	f()t	M es0 t	(число s0 называют показателем роста функции f t ).
3)	f()t	M es0 t	(число s0 называют показателем роста функции f t ).
	Изображением оригинала f t называется функция


				F p f t e ptd t	.
				0
	Основные свойства изображений удобно свести в следующую таблицу:

№

Оригинал

Изображение

f t g t

F p G p

f t

pF p f 0

f t

p2F p pf 0 f 0

F p

f t dt

t n f t

F n p

f t

F p dp

f t t

F p e p

f t e t

F p

F p G p

f t g t f g t d

p F p G p

f t g t f t g 0

f t с периодом T

f t e ptdt

1 e

№	Оригинал	Изображение

12	1							1
12	1							p
								p
13	tn						n!
13	tn					pn 1
						pn 1
14	e t						1
14	e t				p
					p

15	sin t
15	sin t			p2				2

16	cos t							p
				p2 2

17	sh t
17	sh t			p2				2

18	ch t							p
	ch t			p2 2
				p2 2

19	t sin t				2 p
19	t sin t
			p2				2 2

20	t cos t			p2				2
20	t cos t		p2				2 2
			p2				2 2

21	t sh t				2 p
21	t sh t		p2 2 2

22	t ch t			p2				2
22	t ch t		p2				2 2
			p2				2 2

Более подробные таблицы приведены, например, в [2], [6], [7].

Тот факт, что F p есть изображение для

f t , записывают кратко так:

F p f t

или f t F p .

Пример 7.1. Найти изображения следующих оригиналов:

1 cost

, 2)

sin

d ,

t2 cost .

Решение. 1). Из таблицы изображений (см. формулы 12, 16 и 6) получим:

1 cost

p2 1

1 cost

2 1

dp ln p

ln p2

ln1 ln

p p

p2 1

2). Из таблицы изображений (см. формулы 15, 6 и 4) получим:

sint

sin

arcctg p

sint

arctg p

arctg p arcctg p,

p 1

3). Из таблицы изображений (см. формулы 20 и 5) получим:

p2 1

2p p2 3

tcost

t2 cost

Важную роль в приложениях играют функции

t 0,

t a,b ,

(t)

t 0,

a, b

t a,b ,

называемыесоответственнофункциейХэвисайдаиединичнойфункциейотрезка a,b .

Единичная функция a, b t отрезка a,b представима в виде

a, b

t a

t b

и имеет изображение

a, b

e pa

e pb.

Пример 7.2. Найти изображение функции

f t ,

заданной

f t

графически (рис. 20).

Решение. Функция

равна сумме двух вспомогательных

функций

f1(t)

f2(t)

(рис.21,

рис.22).

Так

как

0 1

f1(t) (t 1) 1,2 (t) t

1 (t 1) (t 2) ,

f2(t) (t 2),

то

Рис.20

f t (t 1) 1,2 (t) (t 2) (t 1) (t 1) (t 2) (t 2) (t 1) (t 1) (t 2) (t 2).

По таблице изображений (см. формулы 13 и 7) имеем:

t (t)	1	, (t 1) (t 1)	e p	, (t 2) (t 2)	e 2p	.
	p2		p2		p2

Для функции f t получим изображение:

f1 t

f (t)

e p

e 2p

e p e 2p

Пример 7.3. Найти оригинал по заданному изображению:

Рис.21

F p

2p 3

2) F p

p 2

; 3) F p

e 3p

;

p2 4p 13

p 1 p 2 p2 4

(p 1)2

Решение. 1). Выделим

знаменателе

полный

квадрат

f2 t

p2 4p 13 p 2 2

9 и преобразуем функцию

F p

2p 3

2 p 2 7

p 2

;

1 2

p2 4p 13

p 2 2 9

По таблице изображений (формулы 16 и 15) имеем:

Рис.22

cos3t,

sin3t

2cos3t

sin3t.

p2 9

Тогда, используя формулу 8 из таблицы изображений, получим

f (t) 2e

cos3t

sin3t.

p 2

2). Разложим функцию F(p)

на простейшие дроби:

(p 1)(p 2)(p2 4)

p 2

C p D

p 1 p 2 p2 4

p 1

p 2

p2 4

Приведя к общему знаменателю, получим:

p 2 A p 2 p2 4 B p 1 p2 4 Cp D p 1 p 2 .

Равенство верно при любом p : при p 2 имеем 4 24B B 1/6,

при p 1 имеем 1 15A A 1/15,

при p 0 имеем 2 8A 4B 2D D 2/5;

сравним коэффициенты при p3 : 0 A B C C 1/10. Итак,

F(p)		1	1	1	1	p/10 2/5		1	1	1	1		1	p	1	2	.

	15		p 1	6	p 2		15		p 1	6	p 2	10		p2 4	5
						p2 4										p2 4

Тогда, используя таблицу изображений (формулы 14, 15, 16), получим: f (t) 151 e t 16 e2t 101 cos2t 15 sin2t.

3). Запишем		F p в виде			F(p) e 3p		1	и найдем сначала оригинал для
3). Запишем		F p в виде			F(p) e 3p		(p 1)2	и найдем сначала оригинал для
							(p 1)2
функции	1		, используя формулы 13 и 8 из таблицы:
функции	(p 1)2		, используя формулы 13 и 8 из таблицы:
	(p 1)2
				1	t ,	1	t e t t e t t .
				p2	t ,	(p 1)2	t e t t e t t .
				p2		(p 1)2

Тогда, применяя формулу 7 таблицы изображений, получим:

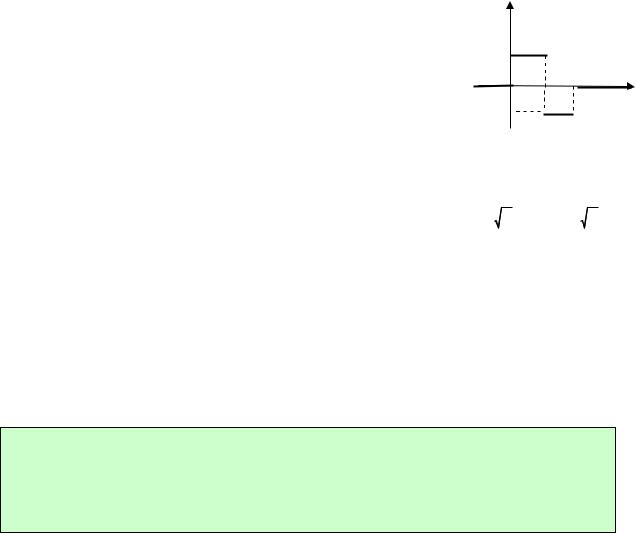
F(p) e 3p	1	t 3 e t 3 t 3 .
	(p 1)2

Примеры для самостоятельного решения

1. Найти изображения следующих оригиналов:

а)

б) sin2 t;

в)

(рис.23).

shtdt;

2. Найти оригинал по данному изображению:

а) F(p)

; б) F(p)

e p

;

в) F(p)

(p 1)2(p 2)

7 p p2

p(p 1)

Ответы: 1.

а)

;

б)

; в)

(1 e p)2

p(p2 1)

p(p2

f t

0	1	2	t
1

Рис.23

2. а)	1	e 2t	et 3tet ;	б) et 1 (t 1) (t 1);	в)	2	3	et/2 sin	3 3	t.
	9					9	2

7.2. Применение операционного исчисления

Использование операционного метода основано на том, что при переходе от оригинала к изображению операции дифференцирования и интегрирования заменяются более простыми операциями умножения и деления. Поэтому операционный метод удобно применять для решения дифференциальных и интегральных уравнений. Для этого следует:

1)перейти от оригиналов к их изображениям (при этом дифференциальные и интегральные уравнения перейдут в алгебраические);

2)из алгебраических уравнений найти изображения;

3)по изображениям восстановить оригиналы.

Решение линейных дифференциальных уравнений с постоянными коэффициентами

Пример 7.4. Решить задачу Коши для дифференциального уравнения:

x x 2 tet 4sint,

x(0) x (0) 0.

Решение. Перейдем в уравнении от оригиналов к изображениям:

0 p

x(t) X(p)

(p 1)2

sint p2 1.

x (t) p

X px 0 x

Используя свойство линейности, получим уравнение относительно изображе-

ния X p :	p2X X	2	4			Отсюда	X(p)	2		4	.
					.
		(p 1)2		p2 1				p 1 2 p2 1	p2	1 2

По изображению восстановим оригинал. Рассмотрим каждое из слагаемых.

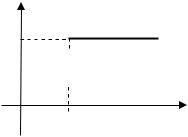
1). Слагаемое

разложим на простейшие дроби:

p 1 2 p2 1

C p D

p 1 2 p2 1

p 1

p 1 2

p2 1

Приведя к общему знаменателю, получим:

2 A p 1 p2 1 B p2 1 Cp D p 1 2 .

Равенство верно при любом p :

при p 1 имеем 2 2B

B 1;

при p 0 имеем

2 A B D.

Сравним коэффициенты при p3 и p2 :

0 A C,

0 A B D 2C .

B 1,

Решим систему

A B D 2,

Получим: C 1,

A 1,

D 0,

B 1.

A C 0,

A B D 2C 0.

Тогда

tet

cost .

(p 1)2(p2

p 1

(p 1)2

p2 1

2). Слагаемое

можно рассматривать как произведение изображений

(p2

1)2

. По свойству об изображении свёртки (формула 9 из таблицы изоб-

p2 1

ражений) получим

4sint sint 4 sin sin(t )d 2 (cos(2 t) cost)d

sin(2 t)

0t 2 cost

t0 2sint 2tcost.

Окончательно имеем x(t) et

tet cost 2sint 2tcost .

Пример 7.5. Решить задачу Коши

f t

x x f (t),

(см. рис.24).

Решение.

x(0) 1,

x (0) 0,

Пусть x(t) X(p), тогда

X p .

x (t)

X px(0) x

(0) p

Рис.24

Найдём изображение функции

f t , представив её в

виде суммы t и t 1 :

f (t) t t 1

e p

Перейдём в исходном уравнении к изображениям и найдём X(p):

p2X p X

1 e p

X p2

p2 1

e p

p p2 1

Восстановим оригиналы, используя таблицу изображений (формулы 12, 15, 4, 7):

1	1 1 t ,	1		1	t	0t 1 cost 1 cost t ,
			sint,		sin d cos


p		(p2 1)		p(p2 1)	0

e p

p p2 1 1 cos t 1 t 1 .

Тогда x t t 1 cos t 1 t 1 .

Решение линейных дифференциальных уравнений с постоянными коэффициентами методом Дюамеля

Метод Дюамеля выгодно применять при решении уравнения со сложной правой частью f t или при решении нескольких уравнений с одинаковыми левыми

и различными правыми частями.

Рассмотрим задачу

		t cx		t f t ,
ax	t bx				(7.1)
			0	0.
	x 0 0, x

Метод Дюамеля решения этой задачи состоит в следующем:

рассмотреть вспомогательную задачу с правой частью, равной единице

t cx t

ax t bx

(7.2)

x1 0 0, x1 0 0;

в задаче (7.2) перейти к изображениям X1 p ap2 bp c

и восстановить

оригинал x t по его изображению pX

;

a p2 bp c

решение исходной задачи (7.1) найти по формуле

x t f t x

d .

2 ,

et 1

Пример 7.6. Решить задачу Коши

0 0.

x 0

0, x

Решение. Для функции f t

изображение найти сложно. Поэтому при-

et 1 2

меним метод Дюамеля. Для этого запишем вспомогательную задачу с правой частью, равной единице:

t x t 1,

0 0.

0 0, x1

Перейдем от оригиналов к их изображениям, полагая x1 t X1 p

и учитывая,

что x1 t pX1 p ,

t p

X1 p , 1

. Получим:

X1 p p2 p

pX1 p

x1 t 1 e t .

p p 1

Решение исходной задачи найдем по формуле

1 e t d

x t f t x1 t f x1 t d

1 1

0 e 1

e 1

e t

2 d

e 1 1 e t

e t

e 1

et 1

1 e

ln e

1 e

e 1

Решение систем линейных дифференциальных уравнений

с постоянными коэффициентами

Операционный метод решения системы линейных дифференциальных уравнений аналогичен методу решения одного линейного дифференциального уравнения. Переходя от оригиналов к изображениям, получим систему линейных алгебраических уравнений; решим ее одним из известных способов, например, методом Гаусса, или по формулам Крамера; затем по найденным изображениям восстановим оригиналы.

Пример 7.7. Решить задачу Коши для системы дифференциальных уравнений:

x y y et,

2x y 2y cost,

x(0) y(0) 0.

Перейдём от оригиналов к изображениям. Пусть x(t) X(p),

y(t) Y(p). Тогда

t pX x 0 p X,

, cost

p 1

p2 1.

y (t) pY,

Дифференциальные уравнения для оригиналов перейдут в алгебраические уравнения для изображений:

	p X pY Y	1					,


		p 1
					p
2p X pY 2Y					p			.
2p X pY 2Y								.
			p	2		1
			p			1

Умножив первое уравнение на 2 и сложив его со вторым, получим

Y (4 p)

или

Y(p)

p2 1

p 1

(p2

1)(p 4)

(p 1)(p 4)

Из первого уравнения

(p 1)

p X

(p 1)Y

или

X(p)

p 1

p(p 1)

(p2 1)(p 4)

p(p 4)

По изображениям восстановим оригиналы:

1 1

e d e

;

2 e

p(p 1)

p(p 4)

Разложим функцию

p 1

на простейшие дроби

p2 1 p 4

p 1

B p C

;

тогда

p 1 A(p2

1) (Bp C)(p 4).

(p2 1)(p 4)

p 4

p2 1

При p 4 имеем 3 17A

A 3/17;

при p 0

имеем

1 A 4C C 5/17.

Приравняем коэффициенты при p2 :

0 A B

B 3/17. Тогда

p 1

cost

sint.

(p2 1)(p 4)

2 1

Окончательно получим

x(t) et 1

e4t

cost

sint или x(t) et

e4t

cost

sint .

Восстановим y t

по его изображению

Y(p)

1 p 4

p 1 p 4

Разложим каждое слагаемое на простейшие дроби:

			p						A1					B1p C1									;													2										D1						D2			.
								p 4															;					(p 1) (p 4)																											.
			(p2 1)(p 4)					p 4							p2 1													(p 1) (p 4)																		p 1					p 4
Получим:		p A (p2 1) (B							1	p C					)(p 4) и															D		1		(p 4) D									2	(p 1) 2.
		1							1				1																			1											2
При p 4		имеем		4 17A				A										4			,			3D			2				2 D										2		2		;
При p 4		имеем		4 17A				A													,			3D							2 D												3		;
					1							1					17																										3
При p 0		имеем		0 A 4C								C								1		,			4D							1		D				2	2							D			1		2		.
При p 0		имеем		0 A 4C								C										,			4D									D					2							D					3		.
					1				1				1						17																										4						3
Сравним коэффициенты при p												2 :			0 A B											1									B	1	A								4		.			Тогда
Сравним коэффициенты при p												2 :			0 A B																				B		A							17			.			Тогда
																					1																					1		17
Y(p)		p			2												4				1							4								p						1			1						2 1					2 1

	(p2 1)(p 4)				(p 1)(p 4)											17				p 4									17						p2		1					17			p2				1			3		p 1		3	p 4
						22			1					4						p							1								1						2			1				;
								p 4					17													17																						;
					51			p 4					17					p2 1								17							p2 1								3 p 1
							y(t)				22		e		4t				2		e	t				4				cost								1		sint.
							y(t)				51		e						3		e				17					cost							17			sint.
											51								3						17												17

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.02.201593.49 Кб63Практика производственная Титов.docx
#
26.09.2019131.58 Кб1Практика профессионально-экономическая 2012.doc
#
10.11.201886.83 Кб13практика рабочая тетрадь 1 Общение.docx
#
29.03.20151.19 Mб41ПРАКТИКА теоретическая механика.docx
#
08.11.2019192 Кб4практика требования 3 курс.doc
#
13.03.20161.17 Mб71Практика ФКП.pdf
#
22.02.2015188.93 Кб13практика.doc
#
22.02.201583.46 Кб14практика.doc
#
22.02.20156.78 Mб71практика.docx
#
03.05.201543.33 Кб64практика.docx
#
22.02.2015872.96 Кб97ПРАКТИКА5.doc