Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Практика ФКП

.pdf

Скачиваний:

Добавлен:

13.03.2016

Размер:

1.17 Mб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Учитывая, что	1		i , получим решения уравнения
		i

z1 2 k iln					1 ,	z2 2 k iln		1 ,	k 0, 1, 2,...
				2			2

3. Дифференцируемыеианалитическиефункции

Функция f z называется дифференцируемой в точке z0 , если она имеет в этой точке производную

f z0	lim	f z f	z0	lim	f z0
		z z0			z
	z z0			z 0

Для функций комплексного переменного справедливы правила дифференцирования суммы, произведения, частного, правила дифференцирования элементарных функций:

u v u v

u v

;

v ,

u v ,

n 1

n z

, sin z

cosz ,

sin z

e ,

cosz

ln z

Кроме элементарных функций, есть другие функции комплексного переменно-

го, например,	z	, Rez2 , Im	z	z3 и т.д. Как проверить их дифференцируемость?
Функция	f z u x,y iv x,y будет дифференцируемой тогда и только то-
гда, когда выполняются следующие условия Коши-Римана:
							.
					ux vy,	uy vx	.
Пример 3.1. Выяснить, являются ли функции а) f (z) z e3 z, б)								f (z) 5	z	3iz
аналитическими в области определения. Если да, то найти их производные.
Решение.	f (z) z e3 z является элементарной функцией,
а). Функция	f (z) z e3 z является элементарной функцией,							определенной на

всей комплексной плоскости; следовательно она является аналитической на комплексной плоскости. Найдём ее производную

z e

3 e

3z 1 .

(z) z e

б). Функция f (z) 5

3 iz

не является элементарной функцией, поэтому сле-

дует проверить выполнение условий Коши-Римана. Для этого запишем функцию в виде

f (z) 5z 3 iz 5(x i y) 3i(x i y) 5x 3y i 5y 3x .

Отсюда действительная часть функции u 5x 3y,					мнимая часть v 5y 3x .
Найдем частные производные этих функций:

	uy 3,		vx 3,	vy	5.
ux 5,
Так как ux vy , то функция	f (z) 5	z	3iz не является аналитической ни в од-
ной точке комплексной плоскости.			11

В теории функций комплексного переменного важную роль играет класс функций, называемых аналитическими. Однозначная функция f z называется

аналитической в области D, если она дифференцируема в каждой точке этой области.

Укажем ряд свойств аналитических функций.

1). Функция f z является аналитической в области D тогда и только тогда,

когда в этой области ее действительная и мнимая части удовлетворяют условиям Коши-Римана.

2). Сумма, разность, произведение, суперпозиция аналитических функций являются функциями аналитическими. Частное аналитических функций является аналитической функцией, если знаменатель не обращается в нуль.

3). Пусть функция f z u x, y iv x, y						является аналитической в области D.
Тогда в этой области функции					u x, y ,	v x, y		являются гармоническими, т.е.
удовлетворяют уравнению Лапласа:
						,			.		(3.1)
				uxx	uyy 0		vxx vyy 0

Отметим, что из гармоничности функций								u x, y , v x, y		не следует анали-
тичность функции			f z u x, y iv x, y .					Например,		для	функции
f z	z	x i y ее действительная и мнимая части u x, y x,								v x, y y	являют-

ся функциями гармоническими, но не удовлетворяют условиям Коши-Римана, т.е. функция f z z не является аналитической.

4). Если известна действительная или мнимая часть аналитической функции	f z ,
то с точностью до постоянной может быть восстановлена сама функция f z .
Пусть, например, известна Re f z u x, y . Требуется найти Im f z v x, y .
Воспользуемся условиями Коши-Римана:	(3.2)
vx uy , vy ux .

Первое из этих равенств проинтегрируем по x с точностью до константы c y , не зависящей от переменной интегрирования

v uy dx c y .

Для отыскания c y следует подставить найденную функцию v x, y во второе из равенств (3.2).

Пример 3.2. Найти, если возможно, аналитическую функцию f z , у которой

Im f z v x, y chx sin y .

Решение.Проверимгармоничностьфункции v x,y :

vxx vyy chx sin y chx sin y 0.

Из гармоничности функции v x,y следует, что она является мнимой частью некоторой аналитической функции f z u x, y iv x, y . Для отыскания функции f z

найдем ее действительную часть из условий Коши-Римана:

ux vy chx cos y,		uy vx shx sin y .		(3.3)

Равенство ux chx cos y проинтегрируем по x:

u chx cos y dx shx cos y c y .

Дляотыскания c y подставимнайденнуюфункцию u x, y вовтороеизравенств(3.3):

			c y c	u shx cosy c .
uy shx sin y shx sin y c y		c y 0
Подставим найденное u x,y	и заданное v x, y		в функцию	f z u iv и выразим
ее через z ,учитывая,что ch iy cos y,		sh iy isin y:

f z u iv shx cos y c i chx sin y shx ch iy chx sh iy sh x iy c shz c.

Следовательно, f z shz c.

4. Интегрированиефункциикомплексногопеременного

Пусть z z t

есть параметрическое уравнение дуги AB , причём концам

дуги A, B соответствуют значения параметров tA, tB.

Тогда

f z dz f z t z t d t

Пример 4.1. Вычислить интеграл

Rezdz по отрезку L

с концами в точках

z1 1 2i, z2 2 3i .

Решение. Уравнение отрезка L с концами в точках z1, z2

имеет вид:

z z1 t z2 z1 , 0 t 1

В нашем случае

z 1 2i t 1 i Rez 1 t,

dz 1 i dt ,

1 t 1 i dt 1 i

1 i .

Rezdz

Пример 4.2. Вычислить интеграл

zImz2dz, если контур L задан соотноше-

(L)

ниями Rez 1,

Im z

то уравнение контура L можно записать

Решение. Так как Rez x,

Imz y ,

следующим образом: x 1,

или x 1,

2 y 2. На линии L имеем:

z x i y 1 i y, Imz2 Im(1 i y)2 2y,

dz idy.

2i y i y2 dy

Тогда zImz2dz (1 i y)2yidy

(L)

Пример 4.3. Вычислить интеграл

dz по границе

области D : Re z 0,

(L)

Im z 0.

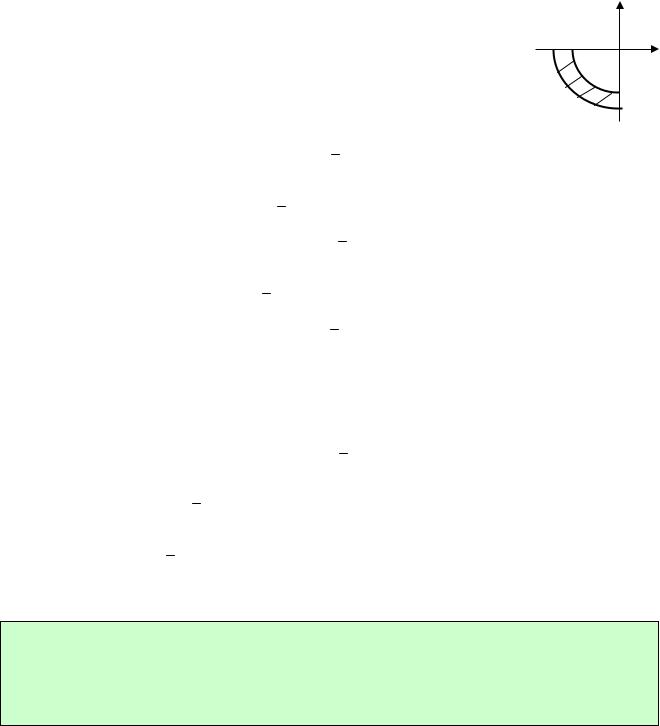
Решение. Изобразим область D на плоскости z (рис.6).

Граница области – линия L – состоит из двух дуг окружно-

стей (дуги BC и FA) и двух отрезков ( AB и CF ), следовательно, интеграл по контуру L будет равен сумме четырёх инте-

гралов. Выберем обход контура против часовой стрелки. Вычислим каждый из интегралов.


1). На отрезке AB имеем: y 0,	z x,		z	x,		dz dx, и
	z		3
		dz		x	dx 1.
	z			x
AB			2

		y	z
B	A
3	2	0	x
		2 F
		3 C
		Рис. 6

2). На отрезке CF

имеем: x 0,

z i y,

i y,

dz idy,

y [ 3, 2] и

i y

i dy i.

i y

3). На дуге BC имеем:

3, z 3ei ,

3e i ,

dz 3iei d , , 3 /2 и

3 /2

3iei d

e3i 3id e3i

3 /2

BC z

isin

cos3 i sin3 1 i.

cos

4). На дуге FA

имеем:

z 2ei ,

2e i ,

dz 2iei d и

2ie3i d

e3i

( 1 i).

3 /2

Следовательно,

dz 1 i 1 i

1 i

1 i .

(L)

Интегральная теорема Коши

Пусть функция f z является аналитической в односвязной области D.

Тогда интеграл от этой функции по любой замкнутой кривой L из области D равен нулю, т.е. f z d z 0 .

Если функция является аналитической в односвязной области, но линия

интегрирования незамкнута, то интеграл	f z dz не зависит от формы
AB
B
кривой. Такой интеграл обозначают f z dz	и к нему применимы такие же
A

методы вычисления, как при интегрировании функции действительной переменной, например, метод подведения под знак дифференциала, метод интегрирования по частям.

Пример 4.4. Вычислить интеграл

zez2dz:

(L)

а) по дуге L параболы y x2

от точки z

до точки z

1 i,

б) по отрезку L2 прямой, соединяющему эти точки.

Решение. Так как функция f (z) zez2

аналитична всюду на комплексной плос-

кости, то

zez2dz не зависит от формы пути интегрирования, т. е.

(L)

1 i

zez

dz zez

d z

e(1 i)

(L1)

(L2)

e2i 1

(cos2 1)

sin2.

Пример 4.5. Вычислить интеграл

5 z2 z cosz

dz.

1 z

z 3

Решение. Подынтегральная функция не определена в точках z i, z 3.

По-

строим контур интегрирования

z 3

1. Это есть окружность с центром в точ-

ке z 3

радиусом 1

(рис. 7).

Особые

точки

функции

z 3, z i, z i лежат вне этой окружности. Поэтому внут-

ри окружности функция

f (z)

5 z

z cosz

является ана-

z2 1 z 3 2

i 0

2 3 4

литической и по теореме Коши

5 z2 z cosz

dz 0.

Рис. 7

1 z

z 3

Интегральные формулы Коши

Интегральные формулы Коши можно записать в виде

f z dz

2 i

2 i f a ,

(4.1)

z a

L z a n 1

и использовать для вычисления соответствующих интегралов при условии, что

точка a находится внутри контура L, функция

f z является аналитической

внутри контура L.

chz

Пример 4.5. Вычислить интегралы I1

dz,

dz.

z2 1

z 3

z 1

Решение. В первом интеграле нули знаменателя z 1 функции

z2 1

находится вне контура

интегрирования

z 3

(рис. 7); поэтому

Рис. 8

внутри этого контура подынтегральная функция является

аналитической и по теореме Коши интеграл I1

равен нулю.

Во втором интеграле точка

z 1

находится внутри контура интегрирования

z 1	1 (рис.8),поэтомупопервойизформул(4.1) имеем

chz

z 1

dz 2 i

ich1.

1 z2 1

1 z 1 z 1

z 1

Пример 4.6. Вычислить интеграл I

sin

dz.

z 3

Решение. Внутри контура

функция

sin

является аналитической, так

z 3

как особая точка z 3 находится вне контура. Поэтому по второй из формул (4.1) при n 1 имеем

2 i

2 i cos

sin

cos

z 1 z

z 3

z 0

z 3 z 3

z 0

3 9

Пример 4.7. Вычислить интеграл I

Решение.

3 z2 2 i z 2i

Нули знаменателя

z1 i,

z2 2

легко находятся

по теореме

Виета.

Поэтому

функция

разлагается на

множители

z2 2 i z 2i 3

z i 3 z 2 3 .

Точки

z1 i,

z2 2

находятся внутри контура

(рис. 9). Построим окружности

1, 2

центрами

в этих

точках

достаточно

малых

радиусов, таких,

чтобы

окружности не пересекались и целиком лежали внутри контура . В многосвязной

области, ограниченной внешним контуром

и внутренними контурами

1, 2 ,

подынтегральная функция является аналитической (т. к. нули

знаменателя не входят в эту область),

поэтому по теореме Коши z

для многосвязной области интеграл по внешнему контуру равен

сумме интегралов по внутренним контурам:

z i

z 2

z i

z 2

i z 2

В интеграле по кривой 1 ,

окружающей точку z1

i, в знаменателе

Рис. 9

оставим z i 3 , а в интеграле по кривой

2 , окружающей точку

z2 2, в знаменателе оставим z 2 3

и применим для каждого интеграла вторую

из формул Коши (4.1) при n 2:

z 2 3

z i 3

2 i

z 2

z i

z i 3

z 2 3

z 2

i 3 4 z 2

z i

12 i

z i

z 2

i 2 5

2 i 5

Примеры для самостоятельного решения

Вычислить интеграл

dz ,

где L :

argz

Ответ:

2 i.

(L)

Вычислить интеграл

по границе

области

/2 argz

(L)

(обход контура против часовой стрелки).

Ответ: i/2.

3. Вычислить (z 1)coszdz

по отрезку z1z2 :

/ 2,

z2 / 2.

Ответ:

-2.

(L)

Вычислить интеграл

ez cosz sin z2 5z 3

dz.

Ответ:

z2 5z 6

z 1

5.Ряды в комплексной области

5.1.Числовые ряды

Необходимый и достаточный признак сходимости ряда:

ряд zn

xn i yn сходится

ряды

xn , yn сходятся.

n 1

Пример 5.1. Исследовать ряд

на сходимость и найти его сумму.

2n !

n 1

n 0

1 n

Решение. Ряд

является знакочередующимся и сходится по признаку

n 0

2n !

Лейбница, так как его члены по абсолютной величине убывают и стремятся к нулю. Для вычисления его суммы запишем ряд Тейлора для функции cosx:

1 n x2n

cosx 1

...

n 0

2n!

1 n

В частности, при x 1 получим n 0

cos1.

2n !

Ряд

является геометрической прогрессией с первым членом

, зна-

n 1

n 0

1/3

менателем

и суммой

. Таким образом, ряд

1 1/3

2n !

n 1

1 q

n 0

сходится и его сумма S cos1

i .

27n

Пример 5.2. Исследовать ряд

на сходимость.

n 1

Решение. Ряд

сходится как эталонный ряд

при p 1.

n 1

n 1 n

Ряд

27n 5

ведет себя также, как ряд

27n

, т.е. сходится.

n 1

3n 1

n 1

n 1n

Следовательно, исходный ряд сходится.

сходится, то lim zn 0.

Необходимый признак сходимости ряда: если ряд zn

n 1

3n4 1

Пример 5.3. Исследовать ряд

на сходимость.

n 1 lnn

10n

Решение. Так как

3n4

то заданный ряд

lim zn

lim

расходится.

n lnn

10n4

n 10n4

Достаточный признак сходимости ряда: если ряд

сходится, то ряд zn

n 1

сходится и называется абсолютно сходящимся рядом.

1 i 2n

Пример 5.4. Исследовать ряд n 1

на сходимость.

cos in

Решение. Рассмотрим ряд из модулей

1 i 2n

1 i

cos in

chn

en e n

e n

n 1

2 n

Ряд

ведет себя также,

как ряд

Последний ряд

n 1 en e n

n 1 en

n 1

сходится, как геометрическая прогрессия со знаменателем q

меньшим

единицы. Поэтому исходный ряд сходится абсолютно.

5.2. Степенные ряды

Степенной ряд в комплексной области есть ряд вида

a1 z z0 a2 z z0 2 ... ,

an z z0 n a0

n 0,1,2,3,... ,

n 0

где an

z, z0 комплексные числа.

Степенной ряд в комплексной области обладает следующими свойствами.


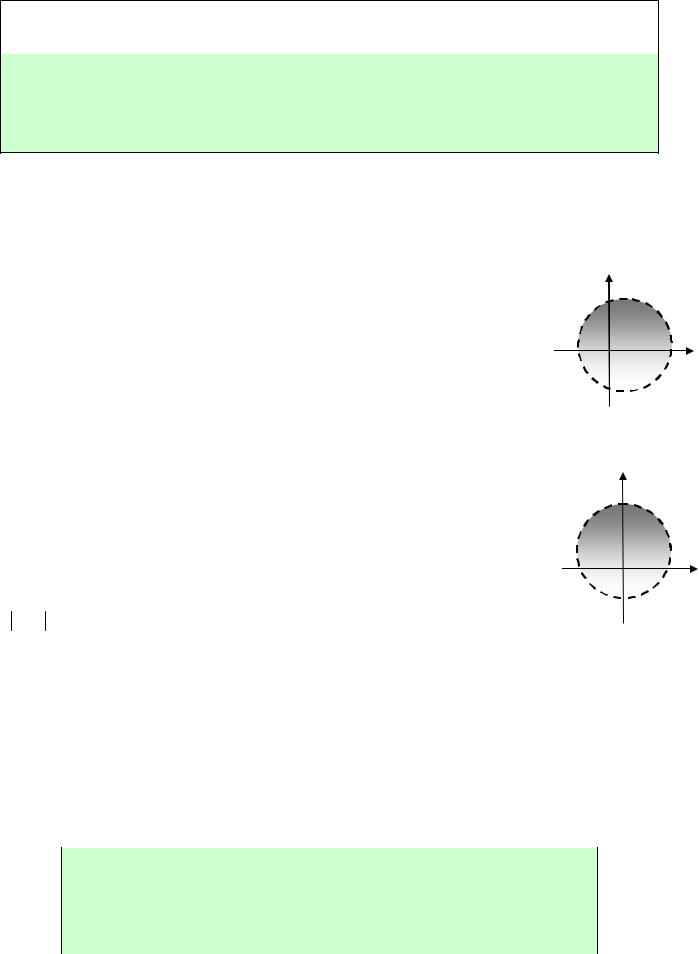
1). Областью сходимости степенного ряда an z z0 n является круг	z z0	R.
n 0

2). Сумма степенного ряда внутри круга сходимости является функцией аналитической.

3). Степенной ряд внутри круга сходимости можно почленно дифференцировать любое число раз и почленно интегрировать.

Пример 5.5. Найти и построить область сходимости ряда

z 2

n 0

4 3i

z 2

Решение. Ряд является геометрической прогрессией со знаменателем q

4 3i

Поэтому ряд сходится, если

1 , т.е.

z 2

4 3i

0 2

Областью сходимости ряда является круг с центром в точке z0 2

и радиусом R 5 (рис. 10).

z i n .

Пример5.6.Найтиипостроитьобластьсходимостиряда

Рис. 10

n 0

Решение. Применим признак Даламбера для ряда из модулей:

lim

un 1

lim

n 1

z i

n 1

z i

lim

n 1

z i

3n 1

z i

3 n n

Если

z i

3, то ряд расходится; если

z i

3, то ряд схо-

дится, т.е. областью сходимости ряда

является круг с центром в

точке z0 i и радиусом R 3 (рис. 11). На границе круга, т.е. при

z i 3 нужны дополнительные исследования, которые

Рис. 11

проводить не будем.

5.3. Ряды Тейлора и Лорана

Функция

f z ,

аналитическая

в круге

z z0

разлагается в этом круге в ряд Тейлора по степеням z z0 :

f z Cn z z0 n .

n 0

Функция

f z ,

аналитическая в

кольце

z z0

R ,

разлагается в этом кольце в ряд Лорана по степеням z z0


f z	Cn z z0 n .
	n
	19

3)2 4 ln 4 1

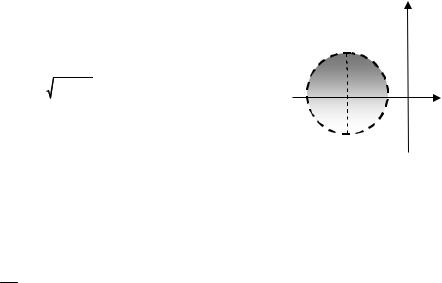
Ряды Лорана и Тейлора внутри их области сходимости можно почленно интегрировать и дифференцировать, при этом область сходимости вновь полученных рядов не изменится.

При разложении функции в ряд сначала нужно найти область сходимости; для этого не надо использовать признак Даламбера (в отличие от функции действительного переменного); достаточно найти круг или кольцо аналитичности функции.

Пример 5.7. Функцию f (z) ez2 2z разложить в ряд в окрестности точки z0 1. Указать область сходимости полученного ряда.

Решение. Функция f (z) ez2 2z является аналитической на всей комплексной плоскости, следовательно, её можно разложить в ряд Тейлора по степеням z z0

в круге

z z

. Преобразуем функцию

f (z) ez2 2z

e(z 1)2 1 e 1 e(z 1)2 и вос-

пользуемся известным разложением функции ez

;

. Получим

n 0

(z 1)2n

f (z)

e(z 1)

z 1

n 0


Пример 5.8. Разложить в ряд по степеням z 3 функцию					z
f (z) ln z2 6z 13 ; указать область сходимости ряда.
Решение. 1). Найдем сначала точки, где функция не определена:
z2 6z 13 0 z 3			3 2i
	9 13
Расстояние от этих точек до точки z0 3 равно 2 (рис. 12). По-
этому функция f (z) аналитична в круге		z 3		2 и разлагается в

этом круге в ряд по степеням z 3 .
2). Преобразуем функцию

3 2i

3 0

3 2i

Рис. 12

f (z) ln z2 6z 13 ln (z

Известно, что ln(1 z) ( 1)n 1 zn . Тогда n

n 1

(z 3)2		(z 3)2
	ln4 ln 1		.
4		4

(z 3)2

(z 3)2n

f (z) ln4 ln 1

ln4

( 1)n 1

, если

z 3

n 1

Пример 5.9. Функцию f (z)

z 2

разложить в ряд по степеням z .

z 3

Решение.

Функция f (z)

имеет особую точку

z 3, следовательно, является

аналитической а) в круге

б) в кольце 3

. Найдём ряды для функ-

ции f (z)

в каждой из этих областей, выделив сначала целую часть функции:

f (z)

z 2

z 3 5

z 3

а). Для разложения в круге

3 в знаменателе из двух величин z

и 3 вынесем

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.02.201593.49 Кб63Практика производственная Титов.docx
#
26.09.2019131.58 Кб1Практика профессионально-экономическая 2012.doc
#
10.11.201886.83 Кб13практика рабочая тетрадь 1 Общение.docx
#
29.03.20151.19 Mб41ПРАКТИКА теоретическая механика.docx
#
08.11.2019192 Кб4практика требования 3 курс.doc
#
13.03.20161.17 Mб71Практика ФКП.pdf
#
22.02.2015188.93 Кб13практика.doc
#
22.02.201583.46 Кб14практика.doc
#
22.02.20156.78 Mб71практика.docx
#
03.05.201543.33 Кб64практика.docx
#
22.02.2015872.96 Кб97ПРАКТИКА5.doc