
- •Содержание
- •Введение
- •Содержание учебной дисциплины
- •Раздел 1. Основы теоретической механики. Статика
- •Тема 1.1 Основные понятия и аксиомы статики.
- •Тема 1.2 Плоская система сходящихся сил.
- •Тема 1.3 Плоская система произвольно расположенных сил.
- •Тема 1.4. Центр тяжести.
- •Раздел 2 Кинематика
- •Тема 2.2 Кинематика тела.
- •Раздел 3. Динамика
- •Тема 3.1 Основные понятия и аксиомы динамики.
- •Тема 3.2 Работа и мощность.
- •Раздел 4. Сопротивление материалов
- •Тема 4.1 Основные понятия, гипотезы и допущения сопротивления материалов.
- •Тема 4.2 Растяжение и сжатие.
- •Тема 4.3 Срез и смятие
- •Тема 4.5 Изгиб
- •Тема 4.6 Сопротивление усталости
- •Тема 4.7 Прочность при динамических нагрузках
- •Тема 4.8 Устойчивость сжатых стержней
- •Раздел 5. Детали машин
- •Тема 5.1. Основные понятия и определения
- •Тема 5.2 Соединения деталей. Разъемные и неразъемные соединения
- •Тема 5.3 Передачи вращательного движения
- •Тема 5.4 Валы и оси, опоры.
- •Тема 5.5 Муфты
- •Требования к оформлению и выполнению контрольных работ
- •Задание на контрольную работу № 1
- •Задачи №№ 1-10
- •Задачи №№ 11-20
- •Задачи №№ 21-30
- •Задача № 31
- •Задача № 32
- •Задача № 33
- •Задача № 34
- •Задача № 35
- •Задача № 36
- •Задача № 37
- •Задача № 38
- •Задача № 39
- •Задача № 40
- •Методические указания по выполнению контрольной работы № 1
- •Задачи №№ 1-10
- •Пример 1
- •Задачи №№ 11 -20
- •Пример 2
- •Задачи №№ 21-30
- •Пример 3
- •Задачи №№ 31-40
- •Пример 4
- •Пример 5
- •Пример 6
- •Пример 7
- •Задание на контрольную работу № 2
- •Задачи №№ 1-10
- •Задачи №№ 11-20
- •Задачи №№ 21-30
- •Задачи №№ 31-40
- •Методические указания по выполнению контрольной работы № 2
- •Задачи №№ 1-10
- •Пример 9
- •Задачи №№ 11 -20
- •Пример 10
- •Задачи №№21-40
- •Пример 11
- •Задание на контрольную работу № 3
- •Задачи №№ 1-10
- •Задачи №№ 11-20
- •Задачи №№ 21-30
- •Задачи №№ 31-40
- •Методические указания по выполнению контрольной работы № 3
- •Задачи №№ 1-20
- •Пример 13.
- •Пример 14
- •Задачи №№ 21-30
- •Пример 15
- •Задачи №№31-40
- •Пример 17
- •Вопросы для самостоятельной подготовки к экзамену
- •Приложения
- •Сталь горячекатаная. Балки двутавровые (по ГОСТ 8239-72)
- •Сталь горячекатная, швеллеры с уклоном внутренних граней полок. Сортамент ГОСТ 8240-72(извлечение)
- •Сталь прокатная, угловая, равнополочная. Сортамент ГОСТ 8509-72 (извлечение)
- •Техническая характеристика шарикоподшипников радиальных однорядных (ГОСТ 8338-75) числовое значение коэффициентов е, X, Y
- •Шарикоподшипники радиальные однорядные
- •Список рекомендуемой литературы
- •Основные источники:
- •Дополнительные источники:
- •Электронные образовательные ресурсы:
|
|
16 Тк max |
|
|
|
16 1200 103 |
|
|
|
|
|
|
|
|
|
|||||||||||||
d 3 |
|
|
3 |
|
|
3 203,82 103 |
5,88 10 58,8мм |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3,14 30 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.39) |
|
|
||||
Получаем d = 58,8 мм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. Определяем диаметр вала из условия жесткости |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 1200 103 |
|
|
|
|
3840 104 |
|
|
||||
|
|
d 4 |
32 Т |
к max |
|
|
|
4 |
|
|
|
4 |
|
|
|
|||||||||||||
|
|
G |
|
|
3,14 6 104 |
0, 02 10 3 |
|
|
|
(2.40) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3, 768 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
4 1019,1 104 |
5, 65 10 56, 5мм |
|
|
|
|
|
|
|
||||||||||||||||||
Получаем d = 56,5 мм.
Требуемый размер сечения получился больше из расчета на прочность, поэтому его принимаем как окончательный, округляя до ближайшего ровного значения d = 60 мм.
Задачи №№21-40
Изгиб является наиболее частым видом нагружения. На изгиб работают большинство элементов кузова, рамы, передач подвижного состава. Прочность элемента, работающего на изгиб обеспечивается правильным подбором формы и размеров сечения.
Задачи следует решать после изучения темы 4.5 "Изгиб" и внимательного разбора примеров 11, 12.
Изгиб - это такой вид нагружения бруса, при котором в его поперечных сечениях возникают изгибающие моменты. В большинстве случаев одновременно с изгибающими моментами возникают и поперечные силы - такой изгиб называют поперечным. Если поперечные силы не возникают, изгиб называют прямым чистым.
Для нахождения опасного сечения строят эпюры Q и Ми. Изгибающий момент Ми в произвольном поперечном сечении
бруса численно равен алгебраической сумме моментов внешних сил, действующих на оставшуюся часть, относительно центра тяжести сечения:
Ми М |
(2.41) |
Поперечная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, действующих на оставшуюся часть:
54
Q F |
(2.42) |
Правило знаков для поперечной силы
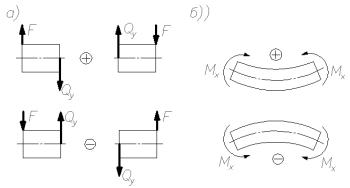
Внешние силы, поворачивающие оставшуюся часть бруса относительно рассматриваемого сечения по ходу часовой стрелки, считаем положительными, а силы, поворачивающие оставшуюся часть бруса относительно рассматриваемого сечения против часовой стрелки, считаем отрицательными (рис. 18а).
Правило знаков для изгибающих моментов.
Внешние моменты, изгибающие края бруса вверх, считаем положительными, а моменты, изгибающие края бруса вниз (рис. 18б) – отрицательными.
Рис.18
Если брус постоянного по длине поперечного сечения, то его размеры подбирают только для опасного сечения – сечения с максимальным по абсолютному значению изгибающим моментом.
Условие прочности для балок, работающих на изгиб имеет вид:
|
Ми |
|
(2.43) |
|
Wх
где Wx – осевой момент сопротивления сечения изгибу относительно оси, перпендикулярной плоскости действия Ми.
Пример 11
Брус, один край которого жестко закреплен, нагружен по схеме (рис.19) силой F = 40 кН, парой сил с моментом М = 20 кНм, равномерно распределенной нагрузкой интенсивностью q = 5кн/м. Рассчитать поперечные силы Q и изгибающие моменты Mи по участкам, по-
55
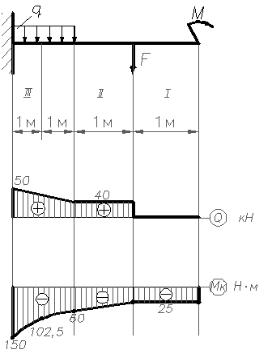
строить эпюры. Подобрать сечение бруса в виде двутавра для наиболее нагруженной точки, если допустимое значение нормального напряжения [σ] = 160 МПа
Рис.19
Ход решения:
1.Разбиваем брус на участки. Границы участков проводим через точки приложения сосредоточенных сил, моментов, начала и конца равномерно распределенной нагрузки. Участки нумеруем от свободного края.
2.Определяем поперечную силу Q по участкам от свободного края, чтобы не определять реакции опор:
Q1 0 |
(2.44) |
Q2 F 40кН |
(2.42) |
Q3 F q z3 |
(2.43) |
Так как на третьем участке Q3 = f (z3) является уравнением наклонной линии, то для построения нужны 2 точки:
при z3.1 0 |
Q3.1 |
40 5 0 40кН |
(2.44) |
при z3,2 |
2м |
Q3,2 40 5 2 50кН |
|
(2.45)
Строим эпюру: проводим базовую линию, перпендикулярно к ней в выбранном масштабе откладываем соответствующие получен-
56
ные значения, через данные точки проводим прямые линии, которые и представляют эпюру Q.
3. Определяем величину изгибающего момента Ми по участкам
|
|
|
|
Ми1 М 20кН м |
(2.46) |
||||||
|
|
|
|
Ми 2 М F z2 |
|
|
|
|
(2.47) |
||
В этом уравнении z2 - переменная величина, поэтому |
определя- |
||||||||||
ется два значения изгибающего момента: |
|
|
|
|
|
||||||
при z2.1 0 |
|
|
Mи 2.1 |
20 40 0 20кН м |
(2.48) |
||||||
при z2.2 |
1м |
Ми 2.2 20 40 1 60кН м |
|
||||||||
(2.49) |
М |
|
М F (z |
|
z ) q z |
|
|
z3 |
|
(2.50) |
|
и3 |
2 |
3 |
|
||||||||
|
|
|
|
3 |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
В это уравнение переменная величина z3 входит в квадрате, поэтому зависимость Mи (z3) графически изображается параболой. Для построения параболы нужно как минимум три точки.
при z3.1 |
0 |
Mи3.1 20 40 1 5 0 60кН м |
(2.51) |
|
при z3.2 |
1м |
Ми3.2 |
20 40 1 1 5 1 0,5 102,5кН м |
(2.52) |
при z3.3 |
2м |
Ми3.3 |
20 40 1 2 5 2 1 150кН м |
(2.53) |
Строим эпюру изгибающих моментов, проводим базовую линию эпюры Ми, в выбранном масштабе откладываем соответствующие полученные значения. На первом участке прямая параллельна оси графика. На втором участке график строится по наклонной линии. Соединяем точки на третьем участке, получаем параболу.
В дальнейшем при построении эпюр изгибающих моментов необходимо помнить, что парабола своей выпуклостью всегда обращена навстречу равномерно распределенной нагрузке.
Для проверки правильности построения эпюр необходимо учитывать следующие правила:
-на участке балки, где отсутствует распределенная нагрузка, эпюра Q – прямая, параллельная базовой линии, а эпюра Ми – наклонная прямая;
-в точках, где приложена сосредоточенная сила на эпюре Q наблюдается скачок, численно равный приложенной внешней силе, а на эпюре Ми – излом;
-в точке приложения сосредоточенного момента на эпюре Ми происходит скачок на размер момента, приложенного в этой точке, а эпюра Q не претерпевает изменения;
-на участке действия равномерно распределенной нагрузки эпюра Q выражается наклонной прямой, а эпюра Ми – параболой, об-
57
ращенной выпуклостью навстречу действию распределенной нагрузки;
- если на участке действия распределенной нагрузки эпюра пересекает базовую линию, то в этом сечении изгибающий момент принимает экстремальное значение;
- изгибающий момент в свободных концевых сечениях бруса всегда равен нулю, за исключением случая, когда в концевом сечении действует сосредоточенная пара сил. В этом случае изгибающий момент в концевом сечении балки равен моменту действующей пары сил.
4. Подбираем номер профиля двутавра из условия прочности при изгибе, если [σ]и = 160 МПа.
max |
|
Ми max |
|
(2.54) |
||
|
||||||
|
|
Wx |
|
|
|
|
отсюда |
|
|
|
|
|
|
|
|
Wx |
Ми max |
(2.55) |
||
|
|
|
|
|||
|
|
|
|
|
|
|
где Wx – осевой момент сопротивления сечения;
Миmax – максимально изгибающий момент, т.е. наибольший по абсолютной величине, определяем непосредственно из эпюры Ми.
Тогда
|
150 106 |
3 |
3 |
|
3 |
(2.56) |
W |
|
937,5 10 мм |
|
937,5см |
|
|
|
|
|
||||
x |
160 |
|
|
|
|
|
|
|
|
|
|
|
По значению Wx = 937,5 см3 по табл. 16 сортамента подходит двутавровый профиль № 40, для которого Wx = 953 см3.
Пример 12
Балка, установленная на двух опорах, нагружена по схеме (рис. 20) силами F1 = 20кН и F2 = 30кН, парой сил с моментом М = 6 кНм. Рассчитать поперечные силы Q и изгибающие моменты Ми, построить эпюры. Для наиболее нагруженной точки подобрать сечение балки, составленное из двух швеллеров, если допустимое значение нормального напряжения [σ] = 150 МПа
58
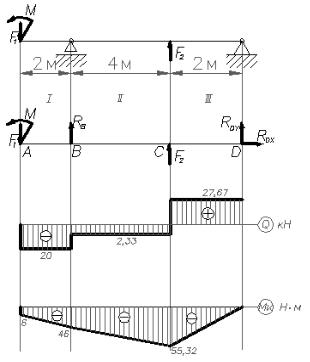
Рис.20
Ход решения:
В отличие от рассмотренного в предыдущем примере бруса, расчет для балки опирающейся на две шарнирные опоры следует начать с определения опорных реакций, исходя из условия ее равновесия.
1. Составим уравнения равновесия:
М B 0 |
|
|
|
М D 0 |
|
|
|
Fx |
0 |
|
|
F1 AB M F2 BC RDy BD 0 |
|
F1 AD M RB BD F2 CD 0 |
(2.57) |
RDx 0 |
|
2. Определим опорные реакции связи:
RDy |
|
F1 AB M F2 BC |
|
20 2 6 30 4 |
27, 67кН |
(2.58) |
|||||
|
BD |
|
6 |
||||||||
|
|
|
|
|
|
|
|
||||
|
|
R |
F1 AD M F2 CD |
|
20 8 6 30 2 |
17, 67кН |
(2.59) |
||||
|
|
|
|
||||||||
|
|
By |
BD |
|
|
6 |
|
|
|
||
|
|
|
|
|
|
|
|
||||
Проверка |
|
|
|
|
|
|
|
|
|
||
|
|
|
Fy 0 |
F1 |
RB F 2 RDy 0 |
(2.60) |
|||||
|
|
|
20 17, 67 30 27, 67 47, 67 47, 67 0 |
|
|||||||
3. |
Определяем поперечные силы по участкам: |
|
|||||||||
|
|
|
|
Q1 F1 20кН |
|
|
(2.61) |
||||
|
|
|
Q2 F1 RB 20 17, 67 2,33кН |
(2.62) |
|||||||
|
|
|
Q3 F1 RB F2 |
20 17, 67 30 27, 67кН |
(2.63) |
||||||
Выполняем проверку:
59
Q3 RDy 27, 67 27, 67кН |
(2.64) |
||
Строим эпюру Q (рис. 20б). |
|
||
4. Определяем изгибающие моменты по участкам: |
|
||
|
Сечение1-1 |
|
|
|
|
Ми1 M F1 z1 |
(2.65) |
при z1.1 0 |
Ми1.1 6 20 0 6кН м |
(2.66) |
|
при z1.2 |
2м |
Ми1.2 6 20 2 46кН м |
(2.67) |
|
Сечение 2-2 |
|
|
|
Ми 2 М F1 (z1 z2 ) RВ z2 |
(2.68) |
|
при z2.1 0 |
Ми 2.1 6 20 (2 0) 17,67 0 46кН м |
(2.69) |
|
при z2.2 4м |
Ми 2.2 |
6 20 (2 4) 17,67 4 55,32кН м (2.70) |
|
|
Сечение 3-3 |
|
|
Ми3 М F1 (z1 z2 z3 ) RВ (z2 z3 ) F2 z3 |
(2.71) |
||
при z3.1=0 Ми3.1 6 20 (2 4 0) 17,67 (4 0) 30 0 55,32кН м |
(2.72) |
||
при z3.2 = 2м Ми3.2 6 20 (2 4 2) 17, 67 (4 2) 30 2 166 166, 0 0 (2.73)
Выполняем проверку: |
|
|
|
Ми3 RD z3 |
(2.74) |
при z3.1 0 |
Ми3.1 27,67 0 0 |
(2.75) |
при z3.2 2м |
Ми3.1 27,67 2 55,34кН м |
(2.76) |
Эпюра Ми изображена на рис. 20в.
5. Подбор сечения осуществляется из условия прочности. Определяем момент сопротивления для наиболее нагруженной точки:
|
Ми max |
|
55,34 106 |
3 |
3 |
|
3 |
|
|
Wх |
|
|
|
|
368,93 10 мм |
|
368,93см |
|
(2.78) |
|
|
150 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Момент сопротивления одного швеллера
60
Wx1 |
|
Wx |
|
368,93 |
184, 47см3 |
(2.79) |
|
|
2 |
|
|||||
|
2 |
|
|
|
|
||
6. По табл. 16 сортамента ГОСТ 3240-72 выбираем швеллер № 18, для которого
|
Wx№22 192см3 |
(2.80) |
|||
При этом профиле рассчитаем напряжение в наиболее нагру- |
|||||
женной точке: |
|
|
|
|
|
|
Ми max |
|
55,34 106 |
|
|
|
|
|
|
144,11МПа |
(2.81) |
2 W |
2 192 103 |
||||
|
x№22 |
|
|
|
|
Проверим на прочность в сравнении с допускаемым напряжени-
ем [σ]
|
|
|
|
144,11 150 |
|
|
|
|
100 % |
100 3,92% |
(2.82) |
||
|
|
150 |
||||
|
|
|
|
|
Вывод: балка недогружена на 3,92 % т.е. менее 10 %, что допускается при практическом конструировании.
61
