. Эйлеровы графы
локальные характеристики графа
историческая справка
эйлеровы и квазиэйлеровы графы
локальные характеристики графа
1.
Определение:
Пусть
x
N
- вершина графа G=(N, A), поставим ей в
соответствие три числа deg+x, deg-x, deg*x:
deg+x - число входящих в x дуг,
deg-x - число выходящих из x дуг,
deg*x=deg+x + deg-x.
deg+x называют полу степенью захода в вершину x, deg-x - полу степенью исхода из вершины x, deg*x - называют степенью вершины x.
Пример
G:
Рисунок 3.4.1.
deg+s=1 deg-s=1 deg*s=2
deg+t=2 deg-t=2 deg*t=4
deg+m=2 deg-m=2 deg*m=4
deg+k=2 deg-k=1 deg*k=3
deg+z=3 deg-z=2 deg*z=5
deg+f=1 deg-f=2 deg*f=3
deg+y=2 deg-y=3 deg*y=5
Теорема (теорема Эйлера о рукопожатиях)
В любом конечном графе G=(N, A) число вершин нечетной степени четно или равно нулю.
2. Будем рассматривать задачи, которыми занимался Леонард Эйлер. Отправной точкой для него послужила знаменитая задача о Кенигсбергских мостах.
Семь мостов города Кенигсберг (точнее Калининград) расположены на реке Прегель так, как изображено на рисунке, соединяя его (города) части A, B, C, D.
Рисунок 3.4.2.
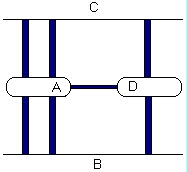
Задача состоит в следующем: Найти такую точку города, выйдя из которой можно пройти по всем мостам города по одному разу и вернутся в нее обратно.
Эйлер показал, что эта задача не имеет решения. Каждый мост Эйлер заменил линией, соединяющей точки, соответствующие берегам. В результате получился граф, изображенный на рисунке:
Рисунок 3.4.3.
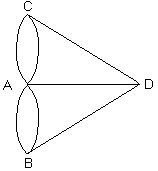
3. Определение:
Связный граф называется Эйлеровым, если на нем существует простой цикл, проходящий через все дуги графа по одному разу.
Рисунок 3.4.4.
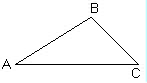
Теорема (Критерий Эйлеровости)
Для того чтобы конечный связный граф был эйлеровым необходимо и достаточно, чтобы степени его вершин были четными.
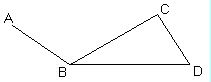
Пример
Можно ли нарисовать, не отрывая карандаш от бумаги и не проходя ни по одному из отрезков дважды и вернутся в начальную точку.
Рисунок 3.4.5.
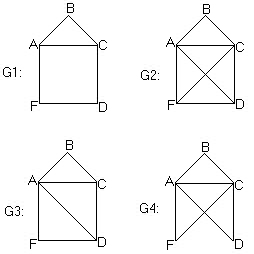
Ответ да для графа G4, т.к. G4 является эйлеровым графом: deg A=4, deg B=2, deg C=4 deg D=2 deg F=2
Определение:
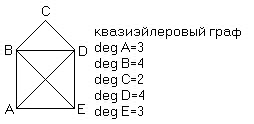
Связный граф называется квазиэйлеровым если на нем существует простая цепь, проходящая через все дуги графа
Рисунок 3.4.6.
Теорема (Критерий квазиэйлеровости)
Для того чтобы конечный связный граф был квазиэйлеровым необходимо и достаточно чтобы степени всех его вершин были четными числами или степени всех его вершин, за исключением равно двух, были четными, причем в первом случае эйлерова цепь является эйлеровым графом, а во втором случае эйлерова цепь начинается в одном из вершин нечетной степени, а заканчивается в другой вершине нечетной степени.
Рисунок 3.4.7.
цепь, проходящая через каждое ребро в точности один раз; для существования Э.ц. необходимо и достаточно, чтобы в графе было ровно две вершины с нечетными степенями.
---11.---
ДЕРЕВОМ называется связный ациклический граф.
Для графа G, являющегося деревом, справедливы следующие утвержде-
ния:
- любые две вершины G соединяются единственным маршрутом;
- граф G связен;
- |V|=|E|+1;
- граф G ациклический и при добавлении в G ребра, связывающего па-
ру несмежных вершин, в полученном графе возникает один простой цикл.
КОРНЕВЫМ ДЕРЕВОМ называется дерево с выделенной вершиной, называе-
мой КОРНЕМ.
ОСТОВНЫМ ДЕРЕВОМ для G=(V,E) называется остовный подграф(V1=V),
являющийся деревом.
ЛЕСОМ называется граф, в котором каждая связная компонента являет-
ся деревом.
ОСТОВНЫЙ ЛЕС для графа G=(V,E) - это совокупность разъединенных
деревьев (соответствующих компонентам связности) Ti=(Vi,Ei), i in Np,
таких, что
p
V=UVi,ViПVj=Ф приi=/=j;Ei<Eдля всехiinNp.
i=1