ЛАБОРАТОРНАЯ РАБОТА №1

Методика оценки погрешностей

Задание 1

1. Найти алгебраическую сумму приближённых чисел. Оценить погрешность.

2. Вычислить приближённо значение выражения 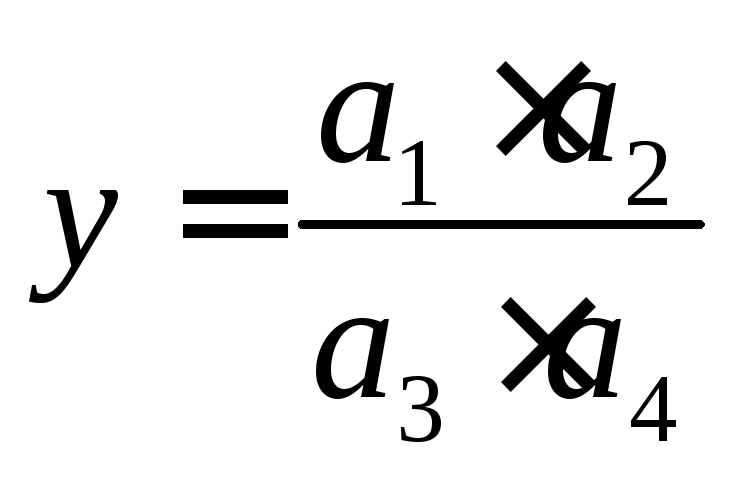. Найти абсолютную и относительную погрешности. Определить количество верных цифр в полученном результате.

3. Вычислить без строгого учёта погрешности значение выражения:

.

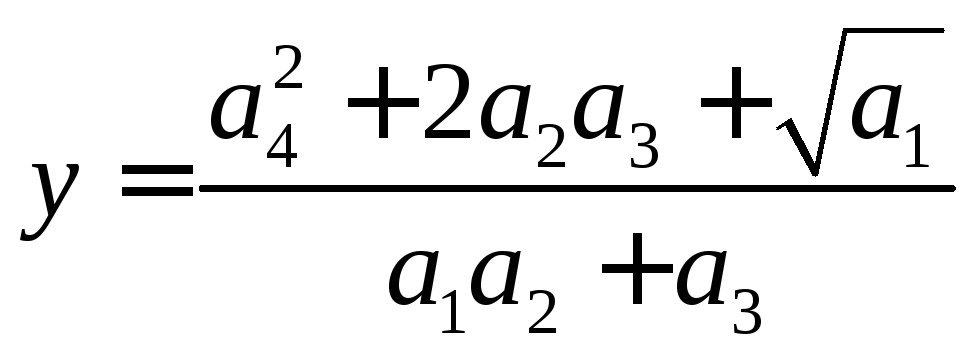Вариант:

Таблица 1

5		765	-8.456	0.217	0.2564
		0.5	0.0002	0.0004	0.00005

Решение.

1. Найдём алгебраическую сумму чисел :

.

Найдём абсолютную погрешность суммы. Так как абсолютная погрешность алгебраической суммы (разности) нескольких приближённых чисел равна сумме абсолютных погрешностей этих чисел, получим

Цифра в записи приближённого числа называется верной в строгом смысле, если её абсолютная погрешность не превосходит половины разряда, в котором находится данная цифра. Тогда приближённая запись полученной суммы имеет вид (в строгом смысле):

.

Найдём относительную погрешность вычисления суммы по формуле , получим

.

2. Используя данные задачи, вычислим значение функции :

.

Найдём относительную погрешность вычислений. Так как относительная погрешность произведения и частного нескольких приближённых чисел, отличных от нуля, равна сумме относительных погрешностей этих чисел, получим:

.

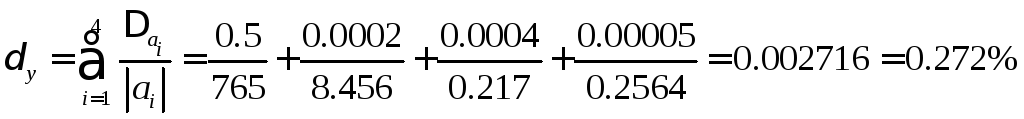Тогда абсолютная погрешность вычисления функции равна

.

Тогда верными в строгом смысле будут три первые цифры полученного значения функции :

.

3. Используя данные задачи, вычислим без строгого учёта значение выражения :

.

Так как точность полученного результата не может быть выше точности наименее точного числа из набора исходных данных (в данном случае наименее точным является число с абсолютной погрешностью), получим

.

Ответ:1.; 2.; 3..

Задание 2

Найти абсолютную и относительную погрешности значения функции при заданной погрешности значения аргумента.

Варианты:

Таблица 2

№	x x
5	1542 1

Решение.Чтобы вычислить значение функциипри данном значении аргумента, переведём градусы в радианы по формулам:

;

.

Получим:

;

.

Вычислим значение функции для полученного в радианах значения аргумента:

.

Абсолютную погрешность функции найдём по формуле:

.

Найдём производную функции :

.

Тогда

.

Следовательно, значение функции можно записать в виде (все цифры верные в строгом смысле):

.

Ответ:.

ЛАБОРАТОРНАЯ РАБОТА №2

Решение нелинейных уравнений

Задание

1. Изолировать корни и для уточнения выбрать первый положительный.

2. Решить уравнение различными методами итерации (простой итерации, касательных и секущих), составить блок-схему алгоритма и программу, получить решение. Оценить погрешность полученных результатов.

Варианты:

Таблица 3

№	Уравнение 1	Уравнение 2
5

Решение.

Уравнение 1:

1. Изолируем корни уравнения геометрически, для этого перепишем уравнение в виде:

.

Построим графики функций и. Так как необходимо найти первый положительный корень уравнения, то графики функций построим на промежутке [0;+):

Точка пересечения этих графиков и есть – искомый первый положительный корень уравнения, и, как видно из графиков, он находится в интервале [1.5,1.75].

Проверим правильность изолирования корня. Для этого найдём значения функции , её первой и второй производных на концах отрезка[1.5,1.75]:

;

;

;

;

; ;

;

.

Полученные данные удовлетворяют теореме Коши о существовании и единственности корня уравнения (функция меняет знак на концах отрезка, а первая и вторая производные – нет), следовательно, корень уравнения изолирован верно.

2. Решим уравнение различными методами итерации.

Метод простой итерации.

Поскольку первая производная , то для нахождения последовательных приближений будем использовать итерационную формулу:

, где при.

То есть получаем итерационную формулу:

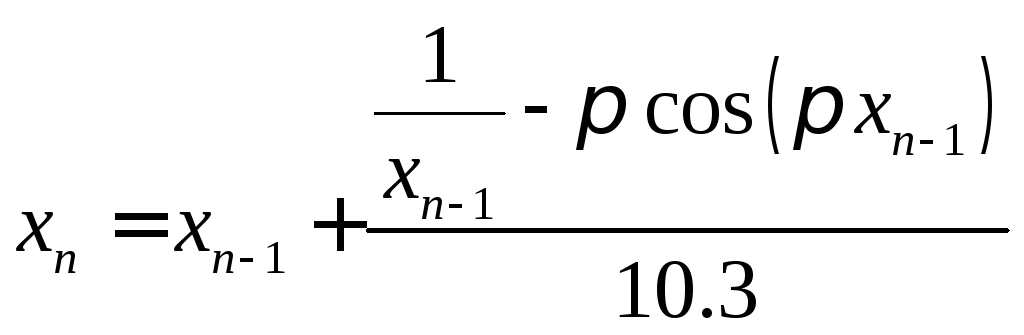или .

Погрешность будем оценивать по формуле

, где .

Получим:

; ;

.

За начальное приближение выберем любое значение промежутка [1.5,1.75], например, .

Подставив это значение в итерационную формулу, получим

, с погрешностью

.

Подставляя последовательно найденные на предыдущем шаге значения в итерационную формулу, будем получать более точные решения уравнения. Вычисления представим в виде таблицы:

n	xn	cos(xn-1)	xn-1cos(xn-1)	Погрешность
0	1,5	0	0
1	1,564725	0,201941	0,992687	0,026537
2	1,565179	0,203337	0,999839	0,000186
3	1,565189	0,203368	0,999996	0,000004

На третьем шаге получаем значение , с точностью, которое примем за решение уравнения(с пятью верными знаками в строгом смысле), и остановим итерационный процесс.

Метод касательных (Ньютона).

Итерационную последовательность будем строить по формуле

.

То есть получаем итерационную формулу:

или .

Погрешность будем оценивать по формуле

, где .

Получим

.

Так как на рассматриваемом отрезке вторая производная положительна, а следовательно , то за начальное приближение выберем.

Подставив это значение в итерационную формулу, получим

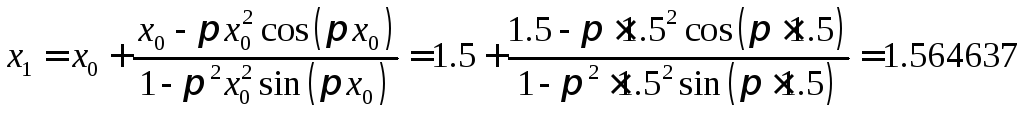, с погрешностью

.

Подставляя последовательно найденные на предыдущем шаге значения в итерационную формулу, будем получать более точные решения уравнения. Вычисления представим в виде таблицы:

n	xn	cos(xn-1)	sin(xn-1)	xn-1cos(xn-1)	x2n-1sin(xn-1)	f(xn)	Погрешность
0	1,5	0	-1	0	-22,2066099
1	1,564637	0,201670	-0,979454	1,551021	-23,665226	0,005562	0,000779
2	1,565189	0,203368	-0,979102	1,565186	-23,673436	0,000001	0,0000001

На втором шаге получаем значение , с точностью, которое примем за решение уравнения(с шестью верными знаками в строгом смысле), и остановим итерационный процесс.

Метод секущих (хорд).

Итерационную последовательность будем строить по формуле

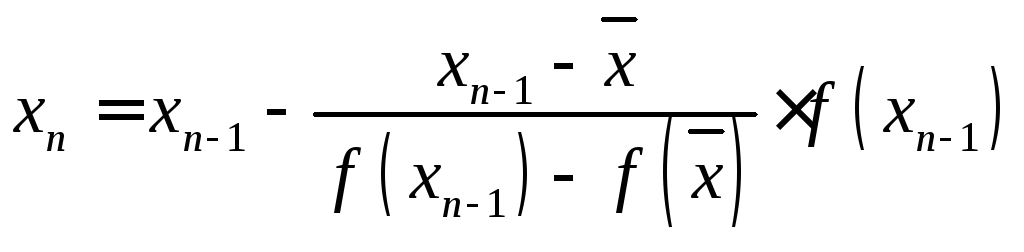, где – координаты неподвижного конца отрезка.

Так как на рассматриваемом отрезке вторая производная положительна, а следовательно , то для соблюдения достаточного условия сходимости метода за начальное приближение выберем, а за неподвижный конец отрезка.

То есть получаем итерационную формулу:

.

Погрешность будем оценивать по формуле

, где .

Получим

.

Подставив значение в итерационную формулу, получим

, с погрешностью

.

Подставляя последовательно найденные на предыдущем шаге значения в итерационную формулу, будем получать более точные решения уравнения. Вычисления представим в виде таблицы:

n	xn	cos(xn-1)	f(xn-1)	Погрешность
0	1,75	0,707107	-1,650013
1	1,571942	0,224093	-0,067854	0,009500
2	1,565296	0,203698	-0,001080	0,000151
3	1,565191	0,203373	-0,000016	0,000002

На третьем шаге получаем значение , с точностью, которое примем за решение уравнения(с пятью верными знаками в строгом смысле), и остановим итерационный процесс.

Уравнение 2:

1. Изолируем корни уравнения геометрически. Построим графики функций и. Так как необходимо найти первый положительный корень уравнения, то графики функций построим на промежутке [0;+):

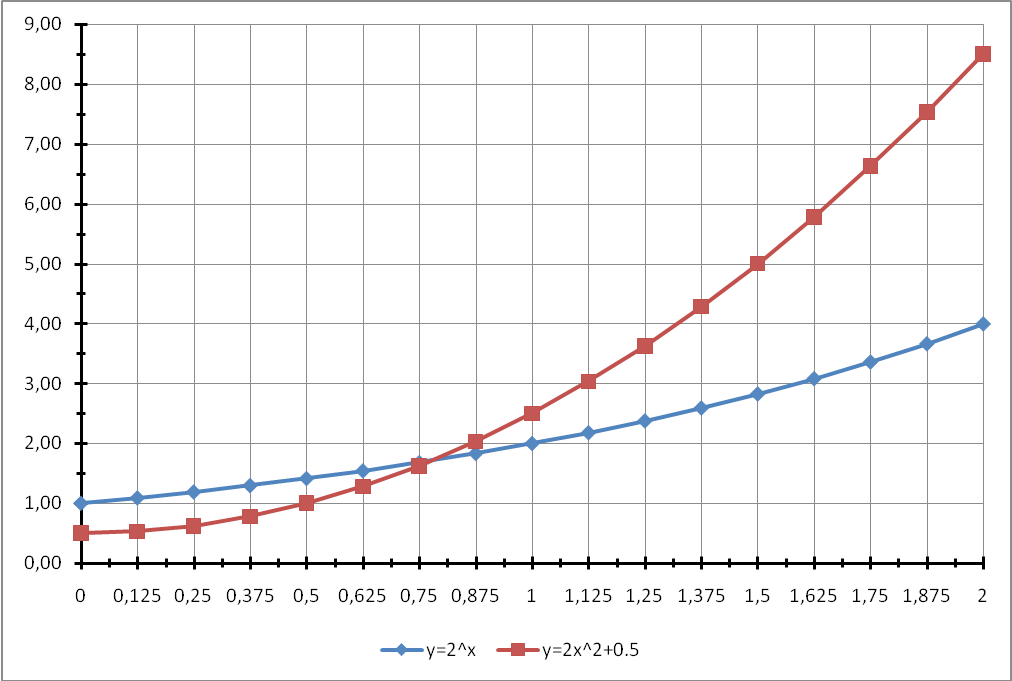
Точка пересечения этих графиков и есть – искомый первый положительный корень уравнения, и, как видно из графиков, он находится в интервале [0.75,1].

Преобразуем уравнение к виду

Проверим правильность изолирования корня. Для этого найдём значения функции , её первой и второй производных на концах отрезка[0.75,1]:

;

;

;;

; ;

; .

Полученные данные удовлетворяют теореме Коши о существовании и единственности корня уравнения (функция меняет знак на концах отрезка, а первая и вторая производные – нет), следовательно, корень уравнения изолирован верно.

2. Решим уравнение различными методами итерации.

Метод простой итерации.

Поскольку первая производная , то для нахождения последовательных приближений будем использовать итерационную формулу:

, где при.

То есть получаем итерационную формулу:

.

Погрешность будем оценивать по формуле

, где .

Получим:

; ;

.

За начальное приближение выберем любое значение промежутка [0.75,1], например, .

Подставив это значение в итерационную формулу, получим

, с погрешностью

.

Подставляя последовательно найденные на предыдущем шаге значения в итерационную формулу, будем получать более точные решения уравнения. Вычисления представим в виде таблицы:

n	xn	2xn-1	2x2n-1+0.5	Погрешность
0	0,75	1,681793	1,625
1	0,771843	1,707450	1,691484	0,009174
2	0,777984	1,714733	1,710518	0,002579
3	0,779605	1,716661	1,715568	0,000681
4	0,780025	1,717161	1,716879	0,000177
5	0,780134	1,717290	1,717217	0,000046
6	0,780162	1,717323	1,717305	0,000012
7	0,780169	1,717332	1,717327	0,000003

На седьмом шаге получаем значение , с точностью, которое примем за решение уравнения(с пятью верными знаками в строгом смысле), и остановим итерационный процесс.

Метод касательных (Ньютона).

Итерационную последовательность будем строить по формуле

.

То есть получаем итерационную формулу:

.

Погрешность будем оценивать по формуле

, где .

Получим

.

Так как на рассматриваемом отрезке вторая производная отрицательна, а следовательно , то за начальное приближение выберем.

Подставив это значение в итерационную формулу, получим

, с погрешностью

.

Подставляя последовательно найденные на предыдущем шаге значения в итерационную формулу, будем получать более точные решения уравнения. Вычисления представим в виде таблицы:

n	xn	2xn-1	2x2n-1+0.5	2xn-1*ln2-4xn-1	f(xn)	Погрешность
0	1	2	2,5	-2,61371
1	0,808701	1,75163	1,808	-2,02066	-0,056360	0,030435
2	0,780809	1,71809	1,719	-1,93234	-0,001231	0,000665
3	0,780172	1,71734	1,717	-1,93032	-0,000001	0,0000003

На третьем шаге получаем значение , с точностью, которое примем за решение уравнения(с шестью верными знаками в строгом смысле), и остановим итерационный процесс.

Метод секущих (хорд).

Итерационную последовательность будем строить по формуле

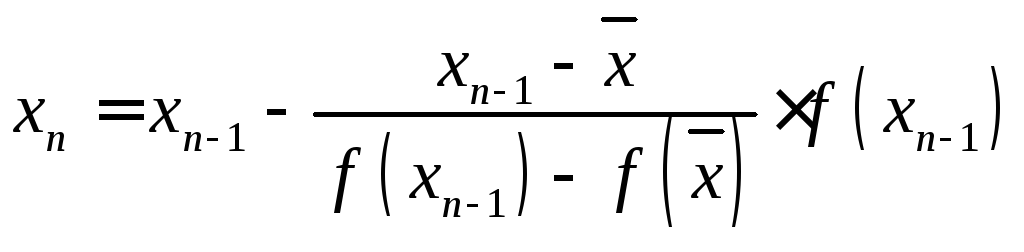, где – координаты неподвижного конца отрезка.

Так как на рассматриваемом отрезке вторая производная отрицательны, а следовательно , то для соблюдения достаточного условия сходимости метода за начальное приближение выберем, а за неподвижный конец отрезка.

То есть получаем итерационную формулу:

или .

Погрешность будем оценивать по формуле

, где .

Получим

.

Подставив значение в итерационную формулу, получим

, с погрешностью

.

Подставляя последовательно найденные на предыдущем шаге значения в итерационную формулу, будем получать более точные решения уравнения. Вычисления представим в виде таблицы:

n	xn	2xn-1-2x2n-1	f(xn)	Погрешность
0	0,75	0,556793
1	0,775500	0,508983	0,008983	0,004851
2	0,779462	0,501369	0,001369	0,000739
3	0,780064	0,500207	0,000207	0,000112
4	0,780155	0,500031	0,000031	0,000017
5	0,780169	0,500005	0,000005	0,000003

На пятом шаге получаем значение , с точностью, которое примем за решение уравнения(с пятью верными знаками в строгом смысле), и остановим итерационный процесс.

Ответ: уравнение 1 ; уравнение 2.

ЛАБОРАТОРНАЯ РАБОТА №3