35589645

РОССИЙСКАЯ КОРРУПЦИЯ: УРОВЕНЬ, СТРУКТУРА, ДИНАМИКА. ОПЫТ СОЦИОЛОГИЧЕСКОГО АНАЛИЗА

ния «среднего» знания среди школьников к задаче оценки среднего значения по закону больших чисел.

Итак, в модельных обозначениях n-й школьник за контрольную по математике получает оценку ξn(M). А это, в силу наших последующих допущений, означает, что его «истинный уровень знаний» характеризуется случайной величиной ζn[ξn(M)]. Математическое ожидание этой величины легко вычисляется и равно

где xu = 0.5 · (au – au–1), так что х1 = 0.075, х2 = 0.25, х3 = 0.5, х4 = 0.75, х5 = 0.925. С другой стороны, в силу закона больших чисел, значения d(M) и

Следовательно, мы можем использовать формулу (2) как «меру знаний» по математике (в среднем по всем школьникам). Более того, так как величины

Qk = (qk(1) · x1 + qk(2) · x2 + qk(3) · x3 + qk(4) · x4 + qk(5) · x5), k = 2, 3, 4 и 5 (3)

можно считать в силу второго допущения одними и теми же для математики и литературы, то формула (2) принимает следующий общий вид

5

k=2

^

где С — код предмета, а d(C) — мера «знаний в среднем» (рейтинг) по этому

pk(M), k 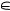{1; 2; 3; 4; 5}, так что остается лишь оцифровать вероятности qk(u), чтобы вычислить Qk по формуле (3). Мы уже обсуждали, что «истинный уровень знаний» ученика, получившего отметку k 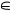{1; 2; 3; 4; 5}, может быть разным. Вероятности qk(u) того, что этот «истинный уровень» находится в интервале Au = {x: au–1 ≤ x < au}, нам неизвестны, но их, как оказалось, можно достаточно хорошо и устойчиво определять экспертно.

В этом модельном примере мы взяли всего два предмета — математику и

130

ГЛАВА 1. МЕТОДЫ ИССЛЕДОВАНИЯ

литературу — и конкретную систему оценок с четырьмя градациями: «плохо» (= 2), «посредственно» (= 3), «хорошо» (= 4) и «отлично» (= 5). Очевидно, что предложенный нами подход пригоден практически при любом числе предметов (объектов сравнения) и при других системах оценок (например, они могут включать градацию «очень плохо» или содержать всего три градации, «плохо», «посредственно» и «хорошо»). В любом из этих гипотетических вариантов исследования мы можем всем оцениваемым предметам приписать рейтинг, меру «знаний в среднем», выявить, с какими предметами дело обстоит очень плохо, с какими — достаточно хорошо, и установить разные другие полезные закономерности различия между предметами и их группами.

ГЕНЕЗИС ОТВЕТОВ РЕСПОНДЕНТА ВО ВРЕМЯ ОПРОСА

Пусть N — число респондентов в опросе, V — табличный вопрос, в котором респондентам предлагается высказать свое отношение к S объектам, используя h градаций. Обозначим m-й объект из списка через Cm и закодируем градации номерами 0, 1, …, h таким образом, что 0 соответствует варианту «З/о» («затрудняюсь ответить»), а порядок базовых, или оценочных, градаций примем таким, что более высокая оценка, с точки зрения позиции на шкале рейтинга, соответствует большему номеру в ряду 0, 1, …, h. Списки градаций могут быть самыми разными — примеры мы приводили выше (см., например, таблицу 1.3.1).

Всякий респондент, выставляя свою оценку z 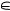{0; 1; …; h} одному из объек-

тов, вообще говоря, реализует свое, весьма «расплывчатое» мнение. Эта «рас-

плывчатость» была бы очевидной, если бы мы попросили оценивать объекты, дав список из большего числа градаций. Например, для шкалы «Согласен — Не согласен» предложили бы респонденту оценить степень его согласия в процентах (100 мелких градаций). Конечно, такого рода «задания» нельзя включать в анкеты опросов общественного мнения, но мы должны понимать, что даже сильно упрощенные варианты этих вопросов являются экспертными и создают определенные трудности при выборе ответа. Однако более существенным является то, что нас интересует не столько конкретный респондент, сколько он же, но как «типичный» представитель той или иной социальной группы.

Дело в том, что представительная выборка для опроса формируется так, чтобы в ней в правильной пропорции были представлены определенные группы населения. Так вот, попавший в нашу выборку человек является представителем некой группы населения (вместе с некоторыми другими респондентами из нашей выборки), и его мнение — это реализация некого размытого, вероятностного мнения целой группы. Математически — это реализация случайного выбора, случайной величины, распределение которой на множестве градаций определяется разнообразием мнений в группе, которую представляет этот респондент.

131

РОССИЙСКАЯ КОРРУПЦИЯ: УРОВЕНЬ, СТРУКТУРА, ДИНАМИКА. ОПЫТ СОЦИОЛОГИЧЕСКОГО АНАЛИЗА

Предположим теперь, что мы можем опросить всю группу населения, которую представляет некий фиксированный респондент из выборки. И пусть все люди из этой группы могут достаточно точно назвать свою оценку на шкале рейтингов [0;1], где 0 соответствует самой «плохой» оценке, а 1 — самой «хорошей». Тогда ответ респондента, который при опросе был случайно извлечен из этой группы, можно представлять как случайный выбор одной из этих оценок и трансформацию этого выбора в одну из градаций.

Другими словами, между оценками на шкале рейтингов [0;1] и оценками из списка градаций имеется неизвестная нам связь, подобная той, какую мы выявили между «истинным уровнем знаний» и отметками, которые получают школьники за контрольную работу.

Если ξn(Cm) — номер градации z 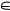{0; 1; …; h}, выбранный n-м респондентом при оценке объекта Cm, и ζn (z| h) — случайная величина, характеризующая «размытость» оценки z при общем числе градаций h, то «истинный уровень измеряемого свойства» (оценку этого объекта n-м респондентом на шкале рейтинга) можно измерять составной случайной величиной ζn (ξn(Cm)|h).

Итак, мы считаем, что отдельный респондент с некими неизвестными нам вероятностями реализует случайный выбор ξn(Cm)= z из спискаградаций {0; 1; …; h}, и что его неизвестная нам оценка на шкале рейтинга [0;1] имеет размытое распределение Fh(x | z), которое можно считать условным распределе-

нием ζn (ξn(Cm)|h) при условии, что ξn(Cm)= z.

В общем случае при оценке разных объектов разными респондентами функция распределения Fh(x| z) не обязана быть одной и той же, так что мы

должны бы снабдить ее индексами m и n, где m — кодовый номер объекта

оценивания, а n — кодовый номер респондента.

Но обратим внимание на следующий чисто математический факт: если имеется N независимых случайных величин τ1, τ2, …, τN , распределенных по законам F1, F2, …, FN , то их чисто случайная перестановка, приводящая к выборке τ’1, τ’2, …, τ’N , дает совокупность уже одинаково распределенных случайных величин с законом распределения

F = N1 · (F1 + F2 + … + FN),

однако сами величины τ’1, τ’2, …, τ’N , оказываются слабо коррелированными,

с коэффициентом корреляции порядка 1 , которым при выборках в несколь-

N

ко сотен респондентов вполне можно пренебречь.

Используя это, мы принимаем в качестве базовой гипотезы допущение о том, что распределение Fh(x | z) зависит только от выбранной градации и от числа градаций h в списке.

Конечно, это всего лишь гипотеза, некая аппроксимация действительности, однако мы все равно должны как-то упрощать ситуацию, чтобы что-то правдо-

132

ГЛАВА 1. МЕТОДЫ ИССЛЕДОВАНИЯ

подобное получить в результате статистического анализа. Нашему оправданию служит еще и то, что наши итоговые рейтинги являются линейными статистическими характеристиками, на значения которых корреляционные связи в выборке почти не влияют: сами значения остаются теми же, но несколько увеличиваются их доверительные интервалы.

Естественно, что все это мы допускаем в пределах одного табличного вопроса, когда список градаций фиксирован, и объекты берутся из одного типологоческого ряда. При этих условиях, если бы к тому же мы знали функции

Fh(x| z), наше вычисление рейтингов можно было бы свести к формуле (4), где

z

wz(h) = 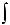xdFh(x| z) (математическое ожидание ζn (z| h)).

0

Это приводит нас к определенной вероятностной модели. А именно, приняв некоторые правдоподобные допущения, мы фактически установили, что при случайном порядке респондентов можно считать, что:

(i) n-й респондент выбирает градационную оценку m-го объекта по закону распределения случайной величины ξn(Cm): он выбирает z 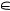{0; 1; …; h} с вероятностями pz(m; h), которые оцениваются наблюдаемыми частота-

Nmz

Nm0 + Nm1 + … +Nmh

дентов, выбравших оценку z;

(ii) если n-й респондент выбрал для оценки объекта Cm вариант ответа z 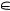{0; 1; …; h}, то его рейтинговая оценка объекта на шкале [0;1] реально

является случайной величиной ζn (z | h) с распределением Fh(x| z), плот-

5-ти интервалов Au = {x: au–1 ≤ x < au}, 0 = a0 <a1 <…<a4 <a5 = 1, и тождественно равна нулю вне отрезка [0;1], причем, qz(1 | h) + qz(3 | h) + …

+ qz(5 | h) = 1.

Отсюда вытекает, что вероятность попадания рейтинговой оценки в Au,

1≤ u≤ 5,поформулеполнойвероятностиравнаg(u| m; h) = h px(m; h) · qx(u| h)

x=0

или, если заменить pz(m; h) на их оценки πz(m; h), то получим оценку для g(u| m; h):

h

z=0

А так как рейтинговые оценки внутри интервала распределены равномерно, то рейтинг объекта оценивается средним значением

133

РОССИЙСКАЯ КОРРУПЦИЯ: УРОВЕНЬ, СТРУКТУРА, ДИНАМИКА. ОПЫТ СОЦИОЛОГИЧЕСКОГО АНАЛИЗА

В результате, мы получили расчетную формулу, в которой неопределенны-

Очевидно, что выбор xz(u| h), 1≤ u≤ 5, — это вопрос об аппроксимации распределений Fh(x | z), и его можно решить в рамках статистической экспертизы и математического моделирования качества этой аппроксимации. А вот выбор дискретных распределений

Q(z; h) = {qz(1 | h), qz(2 | h), qz(3 | h), qz(4 | h), qz(5 | h),},

поставляющих вероятности попадания рейтинговой оценки в интервалы Au, 1≤ u≤ 5, при условии, что случайно взятый респондент выбрал вариант ответа z 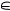{0; 1; …; h}, является существенно более сложной задачей, поскольку нужна социологическая экспертиза связей между градационной оценкой объекта неким усредненным респондентом и его «истинной рейтинговой оценкой» того же объекта.

Другой, чисто математической проблемой, но от этого не менее важной, является вопрос о правомерности выбора математического ожидания в качестве рейтингов. Дело в том, что в рамках модели рейтинг объекта Cm идентифицируется с некоторым распределением Pm на отрезке [0;1], так что задача построения рейтинга — это, одновременно, и задача выбора некой «обоснованной» характеристики для ранжирования этих распреде-

лений. В общем, бóльшим рейтингом должны обладать те распределения,

которые больше смещены к правой границе отрезка [0;1]. А среди таких характеристик «правого смещения» имеется, наряду с математическим ожиданием, целый ряд других. И нужно как-то обосновать, что наш выбор не хуже других.

ОБОСНОВАНИЕ ПАРАМЕТРОВ МОДЕЛИ ДЛЯ ПОСТРОЕНИЯ РЕЙТИНГОВ

Вэтом разделе мы решаем, по сути, три задачи:

(a)обоснование выбора математического ожидания как базовой формулы для рейтинга;

(b)выбор интервалов Au, 1≤ u≤ 5, для конкретизации семейства распределений Fh(x| z);

(c)социологическая экспертиза для выбора условных вероятностей

попадания рейтинговых оценок в интервалы Au, 1≤ u≤ 5, при известной градационной оценке объекта.

Дополнительно к этому мы должны проверить экспертно выбранные пара-

134

ГЛАВА 1. МЕТОДЫ ИССЛЕДОВАНИЯ

метры модели на устойчивость конечных выводов, влияние отклонений на рейтинговый анализ в целом.

Задача (a)

Пусть в рамках модели рейтинг объекта Cm идентифицируется с кусочноравномерным распределением Fm(x ) на отрезке [0;1] таким, что его плотность внутри любого из интервалов является константой, и пусть

pu(m) = Fm(au) – Fm(au–1), 1≤ u ≤ 5.

Влюбом случае мы вынуждены «работать» с этими пятью вероятностями и

счисловыми характеристиками интервалов Au, 1≤ u ≤ 5.

Наиболее простым подходом является поиск линейного рейтинга, представляющего линейную функцию от элементов pu(m). Сложность состоит в содержательном выборе критерия для выбора такой функции. Ниже мы рассмотрим несколько вариантов.

Другая возможность состоит в выборе нелинейных функционалов от pu(m)

или от плотности распределения f (x) = Fʹ(x) . Возьмем, например, весовую

m m

функцию w(x) = (2x – 1)2, которая в большей степени учитывает крайние оценки, чем нейтральные, лежащие в центре отрезка [0;1], и вычислим долю «высоких» оценок по формуле:

характеризующая «вклад» высоких рейтингов (интервалы А4 и А5) по отношению к «вкладу» низких рейтингов (интервалы А1 и А2).

Самый «тривиальный» подход (критерий) состоит в том, что каждому интервалу Аu приписывается фиксированная позиция на шкале рейтингов — его середина xu, 1≤ u ≤ 5, что с учетом частотного веса интервалов автоматически приводит к формуле

Другим критерием для сравнения объектов может быть выбрано среднее значение g(m) градиента роста плотности fm(x) от х = 0 до х = 1. А именно, то значение g, при котором минимизируется интеграл:

135

РОССИЙСКАЯ КОРРУПЦИЯ: УРОВЕНЬ, СТРУКТУРА, ДИНАМИКА. ОПЫТ СОЦИОЛОГИЧЕСКОГО АНАЛИЗА

Оказывается, что минимум достигается при g(m) = 12 · (x^ (m)– 12), так что мы

^

снова приходим к сравнению объектов по величине x(m).

Обратим еще внимание на то, что случайную величину ξ(m), распределенную на отрезке [0;1] с плотностью fm(x) , можно рассматривать как удаленность

^

от самой плохой оценки (нуль на шкале рейтингов), и тогда x(m) — средняя

удаленность от нулевого рейтинга. Аналогичным образом можно построить характеристику, в которой использовалась бы «близость» оценки к наибольшему рейтингу, например, из предположения, что «близость» обратно пропорциональна расстоянию рейтинговой оценки до 1. Соответствующие вычисления приводят к следующему линейному рейтингу:

Y(m) = 15 · (0,46 · p1(m) + 0,544 · p2(m) + 0,82 · p3(m) + 1,64 · p4(m) +

В качестве основного рейтинга нами выбрана следующая величина:

равная при замене pz(m; h) на πz(m; h) величине из (1). Выбор этого индекса обусловлен целым рядом соображений. Заметим только, что сравнение

^

«объектов» проводится фактически по значениям x(m), 1≤ j ≤ s, — величина

^

X(m) отличается лишь линейным преобразованием области значений x(m)

^

в отрезок [0;1], поскольку теоретически x(m) варьирует в меньшем отрезке

[x1; x5], так как 0 < x1 < x5 < 1.

Сравнение рейтингов проводилось как на фактическом материале, так и на смоделированных данных. Итоговый результат можно сформулировать коротко: рассмотренные нами разные типы рейтингов с точностью до линейного преобразования дают практически одну и ту же упорядоченность объектов и практически одни и те же уровни различия между ними.

Мы не будем приводить все эти материалы, а проиллюстрируем полученный результат на одном конкретном примере. Рассмотрим вопрос 10 из опроса граждан в 2001 г.:

136

ГЛАВА 1. МЕТОДЫ ИССЛЕДОВАНИЯ

«В какой степени вы доверяете перечисленным ниже организациям, органам власти? Оцените степень вашего доверия для каждой организации (органа власти), выбрав только один вариант ответа из следующих пяти вариантов: 1 — полностью доверяю, 2 — скорее доверяю, 3 — скорее не доверяю, 4 — совсем не доверяю, 5 — затрудняюсь ответить».

Всего было опрошено 2017 граждан, статистика ответов приведена в таблице 1.3.4. Параметры модельных распределений для этих расчетов были взяты из результатов итогового анализа экспертиз и представлены в таблице 1.3.5.

Согласно таблице 1.3.5, а1 =0.15, а2 = 0.35, а3 = 0.65 и а4 = 0.85, а так как всег-

да а0 = 0 и а5 = 1, то х1 = 0.075, х2 = 0.25, х3 = 0.5, х4 = 0.75 и х5 = 0.925. В строках с вариантами ответов стоят условные вероятности qz(u| h) попадания рейтин-

говых оценок в соответствующие интервалы, причем, здесь h = 4, z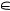{0; 1; 2; 3; 4} (варианты ответов в таблице соответствуют обратному порядку кодов, от 4 до 0) и u, 1 ≤ u≤ 5, — номера интервалов.

Если m — порядковый номер организации (или органа власти), то, обозна-

чая числа в m-й строке символами N1(m), N2(m), N3(m), N4(m), N5(m) и NН/Д(m) соответственно, мы можем определить оценки для вероятностей

интервалов pu(m), 1 ≤ u ≤ 5, по формулам:

где αk(u) — число, стоящее в столбце u-го интервала и в строке k-го варианта

ответа.

Таблица 1.3.4. Частоты ответов на вопрос об оценке 13 организаций, органов власти

137

РОССИЙСКАЯ КОРРУПЦИЯ: УРОВЕНЬ, СТРУКТУРА, ДИНАМИКА. ОПЫТ СОЦИОЛОГИЧЕСКОГО АНАЛИЗА

Пример 1.3.4. Продолжение

Таблица 1.3.5. Вероятности распределения градационных оценок по интервалам

Для проведения реальных вычислений мы должны вместо pu(m) подста-

^

вить вычисляемые их оценки pu (m) в формулы (11), (10) и (7). В итоге мы получим значения рейтингов X(m), Y(m) и D(m) всех 13 объектов сравнения. Дополнительно мы рассчитаем еще один рейтинг

138

ГЛАВА 1. МЕТОДЫ ИССЛЕДОВАНИЯ

Результаты расчетов приведены в таблице 1.3.6, причем, корреляции (линейные связи) между рейтингом Х и рейтингами P, Y и D равны 0.999, 0.995 и 0.999 соответственно, так что все эти рейтинги дадут практически те же самые значения для всех 13 объектов, если их линейно преобразовать так, чтобы совпали рейтинги лишь у 2-х объектов: с максимальным и с минимальным рейтингами.

Таблица 1.3.6. Частоты ответов на вопрос об оценке организаций, органов власти

139