
1 / Алгебра и геометрия / Методички / pdf / Алгебра / Algebra
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования «Гомельский государственный университет имени Франциска Скорины»
А.Д. Ходалевич Р.В. Бородич В.Н. Рыжик
«Алгебра»
Тексты лекций
Гомель, 2004
1
УДК 512 (078) ББК 22.14 Я73 Х 69
Рецензенты: Семенчук В.Н. – доктор физико-математических
наук
кафедра высшей математики учреждения образования «Гомельский государственный университет имени Франциска Скорины».
Рекомендован к изданию научно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины» 24 марта 2004 года, протокол № 7
Ходалевич А.Д.
Х 69 Алгебра: Курс лекций. /А.Д.Ходалевич, Р.В.Бородич,
В.Н.
Рыжик. − Гомель: УО «ГГУ им. Ф.Скорины», 2004. − 37с.
Дается краткое изложение курса лекций по алгебре для студентов, обучающихся по специальности «Прикладная математика»
УДК 512 (078) ББК 22.14 Я73 Х 69
©А.Д. Ходалевич, Р.В. Бородич, В.Н. Рыжик 2004
©Учреждение образования «Гомельский
государственный университет имени Франциска Скорины», 2004
2
СОДЕРЖАНИЕ
1.Комплексные числа……………………………………………4
2.Многочлены и их корни……………………………………….6
3.Матрицы и определители……………………………………..12
4.Системы линейных уравнений………………………………..16
5.Линейные (векторные) пространства…………………………19
6.Квадратичные формы……………………………………….….29
7.Алгебраические структуры………………………………….…32
Литература…………………………………………………………37
3
КОМПЛЕКСНЫЕ ЧИСЛА.
Определение комплексного числа.
Определение. Комплексным числом Z называется выражение вида a + bi, где a, b – действительные числа, символ i удовлетворяет условию i2 = –1.
Число a – действительная часть, bi – мнимая часть, i – мнимая единица комплексного числа.
Множество всех комплексных чисел обозначается С. Таким образом, R C.
Число bi называется чисто мнимым.
Комплексные числа Z1 = a1 + b1i и Z2 = a2 + b2i называются
равными (пишут Z1 = Z2), если a1 = a2 и b1 = b2.
Число Z = 0 + 0i называется нулем и обозначается 0 R.
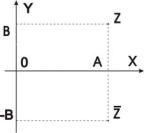
Числа вида a + bi и a – bi называются комплексносопряженными и обозначаются соответственно Z и Z .
Очевидно, что каждому комплексному числу Z = a + bi соответствует единственная точка (a; b) координатной плоскости 0XY. Справедливо и обратное утверждение. Плоскость OXY называется комплексной, оси OX и OY называются соответственно действительной и мнимой.
Действия над комплексными числами.
Пусть даны два комплексных числа Z1 = a1 + b1i и Z2 = a2 + b2i. Суммой Z1 и Z2 называется комплексное число Z = Z1 + Z2 = (a1
+ a2) + (b1 + b2)i.
Разность – это комплексное число Z = Z1 – Z2 = (a1 – a2) + (b1 –
b2)i.
Произведения комплексных чисел Z1 и Z2 называется комплексное число Z = Z1 · Z2 = (a1a2 – b1b2) + (a1b2 + a2b1)i.
Для нахождения |
частного |
Z1 |
знаменатель |
и числитель |
|||||||||||||||||
Z2 |
|||||||||||||||||||||
умножают на |
|
|
2 . Тогда |
|
|
|
|
|
|
|
|
|
|||||||||
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Z1 |
= |
a1 +b1i |
= |
(a1 +b1i)(a2 −b2i) |
= |
(a1 +b1i)(a2 −b2i) |
. |
|||||||||||||
|
Z |
2 |
|
|
a |
2 |
+b i |
|
(a |
2 |
+b i)(a |
2 |
−b i) |
|
a2 +b2 |
||||||
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
2 |
2 |
|
||||||
4
n-ой степенью комплексного числа Z (n N) называется
комплексное число Z n = Z Z ... Z . |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
14243 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
n−раз |
|
|
|
|
|
|
|
|
|
|
|||
Лемма 1.1. |
|
= |
|
+ |
|
; |
|
|
= |
|
|
|
. |
|||||
Z1 + Z2 |
Z1 |
Z2 |
Z1 Z2 |
Z1 |
Z2 |
|||||||||||||
|
Тригонометрическая форма комплексного числа. |
|||||||||||||||||
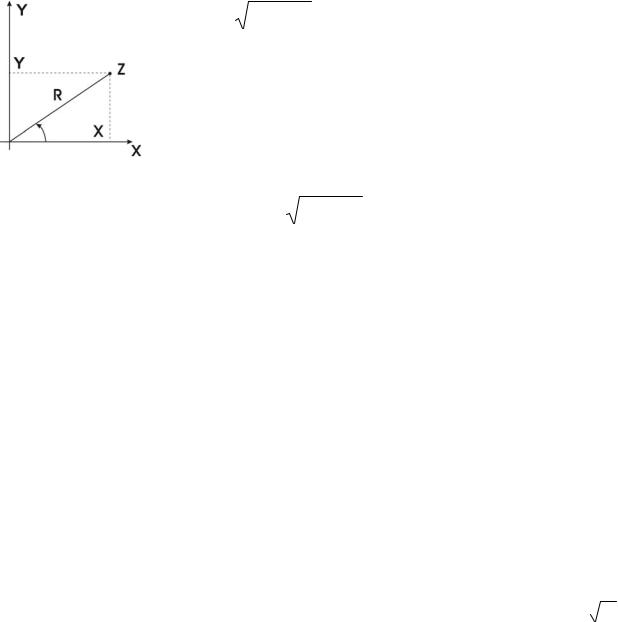
Пусть Z = x + yi и даны прямоугольные прямоугольная и |
||||||||||||||||||
полярная |
системы |
координат. |
|
Тогда |
x = r cosϕ, y = r sinϕ и |
|||||||||||||
следовательно, Z = r(cosϕ +isinϕ) – |
тригонометрическая форма |
|||||||||||||||||
комплексного числа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
r = x2 + y2 |
|
– модуль комплексного числа Z и |
|||||||||||||
|
обозначается |Z|. А полярный угол ϕ - аргумент и |
|||||||||||||||||
|
обозначается arg Z . |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Запись Z = x + yi называется алгебраической |
|||||||||||||||
|
формой комплексного числа. Переход от |
|||||||||||||||||
|
алгебраической |
|
формы |
|
к |
|
|
тригонометрической |
||||||||||
осуществляется по формулам |
|
|
|
|
|
|
|
y |
|
|||||||||
|
|
|
|
| Z |= x |
2 + y2 ; tgϕ = |
. |
||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||
Пусть |
даны |
два |
комплексных |
|
числа |
Z1 = r1 (cosϕ1 +isinϕ1 ) ; |
||||||||||||
Z2 = r2 (cosϕ2 +isinϕ2 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда
Z1Z2 = r1r2 (cosϕ1 +isinϕ1 )(cosϕ2 +isinϕ2 ) =... = r1r2 (cos(ϕ1 +ϕ2 ) +isin(ϕ1 +ϕ2 ).
|
|
Аналогично |
Z1 |
|
= |
r1 |
(cos(ϕ −ϕ |
2 |
) +isin(ϕ −ϕ |
2 |
)). |
|
|
|||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
Z2 |
1 |
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|||
|
|
Индукцией по числу K Z получаем Z k = rk (cos kϕ +isin kϕ) . |
||||||||||||||||
|
|
В |
частности, |
(cosϕ +isinϕ)k |
= cos kϕ +isin kϕ – |
формула |
||||||||||||
Муавра. |
|
|
|
Извлечение корня из комплексного числа. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
Корнем |
n-ой |
степени (n N) из комплексного числа |
||||||||||||||
Z = r(cosϕ +isinϕ) |
|
|
называется |
комплексное |
|
число |
||||||||||||
Z |
0 |
= r (cosϕ |
0 |
+isinϕ |
) , для которого Z n = Z (обозначается Z |
0 |
= n Z ). |
|||||||||||
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|||||
Сравнивая модули и аргументы в последнем равенстве, получаем формулу нахождения всех корней n-ой степени из комплексного числа Z:
5

Z0 = n r (cosϕ +n2πk +isin ϕ +n2πk ) , где k = 0, 1, …, n – 1.
Вывод: существует ровно n различных значений корня n-ой степени из комплексного числа.
Если Z = 1, то 1 = cos0 +isin 0 и n 1 = cos 2πnk +isin 2πnk , k = 0, …,
n – 1.
Корень n-ой степени из 1 называется первообразным, если он не является корнем из 1 с меньшим, чем n натуральным показателем.
Свойства:
Пусть Z1 и Z2 – корни n-ой степени из 1. Тогда:
1)Z1 · Z2 – корень n-ой степени из 1;
2)Z1−1 = 1 – корень n-ой степени из 1.
Z1
МНОГОЧЛЕНЫ И ИХ КОРНИ.
Операции над многочленами
Определение. Многочленом (полиномом) n-ой степени от неизвестного x называется выражение вида
f (x) = a |
xn + a xn−1 |
+... + a |
n−1 |
x + a |
n |
, где ai C, n – целое |
0 |
1 |
|
|
|
неотрицательное число.
Числа ai – коэффициенты многочлена, a0 и an – соответственно старший коэффициент и свободный член. Считаем, что a0 ≠ 0.
Два многочлена f(x) и g(x) одинаковой степени называют равными, если равны их коэффициенты при одинаковых степенях неизвестного (пишут f(x) = g(x)).
Многочлен нулевой степени – это любое отличное от нуля комплексное число. Число нуль – многочлен, степень которого не определена.
Пусть
f (x) = a0 +... + an−1xn−1 |
+ an xn (an |
≠ 0); |
|||
g(x) = b +... +b |
xm−1 |
+b xm (a |
m |
≠ 0); |
|
0 |
m−1 |
|
m |
|
|
Тогда сумма многочленов f(x) и g(x) есть многочлен
f (x) + g(x) = C0 +... +Ck−1xk−1 +Ck xk , где Ci = ai + bi и либо k = n,
либо k = m.
Произведением многочленов f(x) и g(x) называется многочлен
6
f (x) g(x) = d0 + d1x +... + dn+m−1xn+m−1 + dn+m xn+m , где di = ∑ak bl , i
k+l=i
= 0, 1, …, n + m −1, n + m.
Вычитание многочленов определяется как операция, обратная операции сложения. В этом случае противоположным к f(x) является
− f (x) = −a0 −... −an xn .
Для умножения многочленов обратная операция не существует, то есть, нет такого многочлена g(x), что f (x) g(x) =1.
Деление многочленов.
Обозначим степень ненулевого многочлена f(x) через deg f (x) .
Теорема 2.1. (о делении с остатком). Для любых двух многочленов f(x) и g(x) существуют такие единственные многочлены q(x) и r(x), что
f (x) = g(x) q(x) + r(x) и deg g(x) или же r(x) = 0 .
Многочлены q(x) и r(x) называются соответственно частным и остатком от деления f(x) на g(x). Тогда f(x) делится на g(x) или g(x) делит f(x), если остаток r(x) = 0 ( g(x) ≠ 0 ).
Следствие 2.1.1. g(x) является делителем f(x) тогда и только тогда, когда существует многочлен ϕ(x) такой, что f (x) = g(x)ϕ(x) .
Свойства делимости:
1.Если f(x) делится на g(x), а g(x) делится на ϕ(x), то f(x) делится на ϕ(x).
2.Если f(x) и g(x) делится на ϕ(x), то их сумма и разность делится на ϕ(x).
3.Если f(x) делится на ϕ(x), то для любого g(x) на ϕ(x) делится и f (x) g(x) .
4. Если fi(x) делится на ϕ(x) для любого |
i = |
|
, то на |
ϕ(x) |
||||
1,n |
||||||||
делится и многочлен |
|
gi(x) |
|
|
|
|
|
|
fi (x)gi (x) +... + fn (x)gn (x) , |
где |
– |
произвольные |
|||||
многочлены. |
|
|
|
|
|
|
|
|
5. |
Любой многочлен f(x) делится на многочлен нулевой степени. |
|||||||
6. |
Если f(x) делится на g(x), то f(x) делится на ag(x), где a C , |
|||||||
a ≠ 0. |
Пусть f(x) делится |
на g(x). Тогда |
и |
только |
тогда |
|||
7. |
||||||||
deg f (x) = deg g(x), когда g(x) = af (x) , где a C , |
a ≠ 0 . |
|
|
|
||||
7
8. f(x) делится на g(x) тогда и только тогда, когда af(x) делится на g(x) a C , a ≠ 0 .
Наибольший общий делитель. Определение. Многочлен d(x) называется общим делителем
многочленов f(x) и g(x), если он является делителем каждого из них.
Наибольшим общим делителем отличным от нуля многочленов f(x) и g(x) называется такой их общий делитель d(x), который, вместе с тем, сам делится на любой другой общий делитель этих многочленов. Обозначается НОД или (f(x), g(x)).
Если deg( f (x), g(x)) = 0 , то f(x) и g(x) называются взаимно
обратными.
Метод последовательного деления или алгоритм Евклида
заключается в следующей схеме:
f(x) = g(x)q1 (x) + r1 (x),
g(x) = r1 (x)q2 (x) + r2 (x), r1 (x) = r2 (x)q3 (x) + r3 (x),
…………………….
rk−2 (x) = rk−1 (x)qk (x) + rk (x), rk−1 (x) = rk (x)qk+1 (x) + rk+1 (x),
где deg g(x) > deg r1 (x) >... > deg rk (x) ≥ 0.
Теорема 2.2. НОД (f(x), g(x)), где f(x) и g(x) – ненулевые, равен последнему отличному от нуля остатку в алгоритме Евклида, если g(x) не делит f(x), и совпадает с g(x) в противном случае.
Из свойств делимости следует, что НОД (f(x), g(x)) определен лишь с точностью до множителя нулевой степени. Таким образом f(x) и g(x) взаимно простые тогда и только тогда, когда НОД (f(x), g(x)) = 1.
Теорема 2.3. Пусть d(x) = ( f (x), g(x)) . Тогда существуют такие
многочлены u(x) и v(x), что выполняется равенство f (x)u(x) + g(x)v(x) = d(x) .
Причем, если степени f(x) и g(x) больше нуля, то degu(x) < deg g(x) и deg v(x) < deg f (x).
Следствие 2.3.1. (критерий взаимной простоты). f(x) и g(x) взаимно просты тогда и только тогда, когда существуют u(x) и v(x) такие, что
8
f (x)u(x) + g(x)v(x) =1.
Теорема 2.4.
1.Если f(x) взаимно прост с ϕ(x) и h(x), то он взаимно просто с их произведением.
2.Если f(x)·g(x) делится на ϕ(x), но f(x) и g(x) – взаимно просты, то g(x) делится на ϕ(x).
3.Если f(x) делится на g(x) и h(x), и g(x) и h(x) взаимно просты, то f(x) делится на g(x)·h(x).
Теорема 2.5. Пусть f1(x), …, fn(x) – ненулевые и пусть
=( f1 (x), f2 (x)), d3 (x) = (d2 (x), f3 (x)), …,
dn (x) = (dn−1 (x), fn (x)) . Тогда dn (x) – НОД этих многочленов.
Корни многочлена.
Число с называется корнем многочлена f (x) = a0xn +…+ an , если
f (c) = a0cn +... + an = 0 .
Лемма 2.1. Остаток от деления f(x) на x-c равен f(c).
Таким образом, число с тогда и только тогда является корнем f(x), когда f(x) делится на x-c.
Пусть f (x) = (x–c)q(x) + r, и q(x) = b0 xn−1 +... +bn−2 x +bn−1.
Сравнивая коэффициенты при одинаковых степенях, получаем b0 = a0 , b1 = cb0 +a1, b1 = cb0 +a1, … , bk = cbk−1 + ak , r = cbn−1 + an –
схема (метод) Горнера.
Пусть f (x) = (x −c)k ϕ(x) , причем ϕ(x) не делится на x-c. Тогда
число с называется k-кратным корнем f(x), а число k – кратностью корня с в многочлене f(x).
Производной многочлена f(x) называется многочлен (n-1)-ой степени
f ′(x) = na0 xn−1 +(n −1)a1xn−2 +... + 2an−2 x + an−1 .
k-ая производная – это производная от (k–1)-ой производной. Очевидно, что
f (n) (x) = n!a0 , и f (n+1) (x) = 0.
Лемма 2.2. 1) ( f (x) + g(x))′ = f ′(x) + g′(x);
2)( f (x)g(x))′ = f (x)g′(x) + f ′(x)g(x);
3)f (k ) (x) = kf (k−1) (x) f ′(x).
9

Лемма 2.3. Если число с – k-кратный корень f (x), то при k > 1 с является (k – 1) – кратным корнем f ′(x) , если же k = 1, то с не является корнем для f ′(x) .
Основная теорема алгебры.
Любой многочлен с любыми числовыми коэффициентами, степень которого не меньше 1, имеет хотя бы один корень, в общем случае комплексный.
Следствия из основной теоремы.
Лемма 2.4. Пусть f (x)ϕ(x) = g(x)ϕ(x) , ϕ(x) ≠ 0 , тогда
f (x) = g(x). |
|
Теорема 2.5. Для любого многочлена f (x) |
степени n≥1 |
существует единственное разложение |
|
f (x) = a0 (x −α1 )(x −α2 )...(x −αn ) , где αi – корень |
f (x) . |
Следствие 2.5.1. Любой многочлен степени n≥1 имеет ровно n корней, если каждый из корней считать столько раз, какова его четность.
Следствие 2.5.2. Если f (x) и g(x) степени ≤ n имеют равные
значения более чем при n различных значениях неизвестного, то f (x) = g(x).
Следствие 2.5.3. Пусть f (x) ≠ g(x) , тогда существует хотя бы одно число с такое, что f (c) ≠ g(c).
Можно решить обратную задачу. А именно, построить многочлен степени ≤n, принимающий наперед заданные значения при n + 1 различных значениях неизвестного. Например,
f(x) = ∑n+1 ci (x −a1 )...(x −ai−1 )(x −ai+1 )...(x −an+1 ) i=1 (ai −a1 )...(ai −ai−1 )(ai −ai+1 )...(ai −an+1 )
–интерполяционная формула Лагранжа, где ci = f (ai ) и все
ai различны.
Если a0 =1 и все α1,...,αn – корни, то имеют место формулы Виета:
10
