3.6.3. Расчетно-табличный метод минимизации (метод Квайна)

Минимизация этим методом отличается от расчетного только способом выявления избыточных членов в сНДФ. Данный метод предложен американским ученым Квайном, и поэтому называется его именем. Его удобно рассматривать в виде алгоритма с комментариями. Считаем, что минимизируемая логическая функция приведена к СНДФ.

1⁰. Переход от СНДФ к сНДФ. Отыскиваются все простые импликанты. Для этого выписываются все конституенты и все их пары исследуются на возможность склеивания друг с другом. Конституенты, участвующие хотя бы в одном склеивании, отмечаются, но не исключаются из дальнейших сравнений. В результате выявляются импликанты, содержащие по (n-1)-й переменной. С полученными импликантами выполняется та же процедура, что и с исходными конституентами. В результате выявляются импликанты, содержащие n – 2 переменные, и так продолжается до тех пор, пока членов, допускающих склеивание, не останется. Все не отмеченные в процессе указанного преобразования члены представляют собой простые импликанты.

2⁰. Переход от сНДФ к ТНДФ. Дизъюнкция всех простых импликант может содержать избыточные импликанты. Поэтому их надо исключить.

Для этого составляется импликантная таблица, строки которой обозначаются выявленными на 1-м шаге простыми импликантами, а столбцы – конституентами, входящими в СНДФ исходной функции.

3⁰. Расстановка меток. Любая клетка импликантной таблицы отмечается, например, цифрой 1, если она попадает на пересечение конституенты и импликанты, полностью входящей в конституенту.

В каждом столбце при этом может оказаться по нескольку отмеченных клеток. Задача упрощения НДФ сводится к вычеркиванию из таблицы максимального количества строк таким образом, чтобы после этого в каждом столбце осталась, по крайней мере, одна отмеченная клетка..

4⁰. Выделение ядра Квайна (существенных импликант). Выявляются и вычеркиваются столбцы, содержащие только по одной отмеченной клетке. Простые импликанты, соответствующие этим клеткам, вносятся в окончательное выражение НДФ как обязательные члены. Если таких столбцов нет, то переход к п.5⁰, если же есть, то в таблице зачеркиваются строки, соответствующие обязательным простым импликантам и столбцы, содержащие отмеченные клетки в вычеркнутых строках.

5⁰. Поглощение (сжатие) столбцов. Если после этого в таблице окажутся такие пары столбцов, что все отмеченные клетки i-го столбца совпадают полностью или частично с клетками j-го столбца, то j-й столбец вычеркивается. Если таких пар столбцов нет, то переход к п.7⁰, иначе – к п.6⁰.

6⁰. Вычеркивание пустых строк. Строки, не содержащие после выполнения п.п. 4⁰ и 5⁰ ни одной отмеченной клетки, также вычеркиваются.

7⁰. Поглощение (сжатие) строк. Если в таблице имеется такая пара строк, что все отмеченные клетки k-й строки совпадают полностью или частично с отмеченными клетками l-й строки, то k-я строка вычеркивается. Если таких строк нет, то переход к п.8⁰.

8⁰. Получение МНДФ. Для этого импликанты ядра Квайна, т.е. полученные в п. 4⁰ и оставшиеся не вычеркнутыми после выполнения п. 7⁰, соединяются знаками дизъюнкции.

Пример. Минимизировать логическую функцию четырех переменных, заданную в числовой форме . Так как наша цель – рассмотрение процесса преобразования импликантной таблицы, то п. 1⁰ алгоритма выполнять не будем, а выпишем готовые импликанты. Их совокупность будет иметь вид

.

Прочерки в импликантах указывают на отсутствие в них соответствующей переменной.

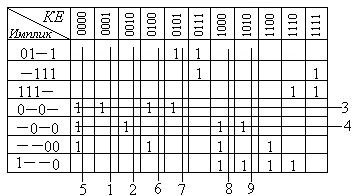
Строим импликантную таблицу (табл.9).

Таблица 9

.

В табл. 9 вертикальные и горизонтальные линии, пересекающие соответствующие столбцы и строки, пронумерованы цифрами. Эти цифры указывают на порядок вычеркивания столбцов и строк.

В соответствии с п. 4⁰ алгоритма устанавливаем, что импликанты 0–0– и –0–0 являются существенными для конституент 0000, 0001, 0100, 0101 и 0000, 0010, 1000, 1010. Они должны быть внесены в МНДФ. Поэтому вместе со 2-м и 3-м столбцами, как содержащими всего по одной отмеченной клетке, вычеркиваем 4-ю и 5-ю строки, а также столбцы 1,4,5,7 и 8, на пересечении с которыми в вычеркнутых строках 4 и 5 стоят единицы.

В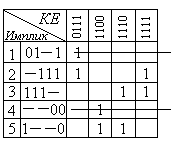результате выполнения этих операций импликантная таблица приобретает вид:

Д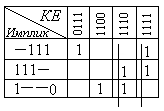алее выполняем поглощение столбцов. Однако это невозможно, так как в таблице нет ни одной пары столбцов, которые бы полностью или частично совпадали. Поэтому в соответствии с п.7⁰ алгоритма выполняем поглощение строк. Видим, что строка 2 поглощает строку 1, а строка 5 – строку 4. В результате получаем таблицу:

С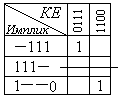нова выполняем поглощение столбцов и получаем таблицу:

Так как в предыдущей таблице получили строку, не содержащую единиц, то, вычеркивая её, получаем окончательную таблицу:

Соединяя импликанты, соответствующие столбцам с одной отмеченной клеткой и оставшиеся в последней таблице, знаком , получим МНДФ:

Достоинством рассмотренного метода Квайна является то, что он применим для любого числа переменных и может быть реализован в виде программы для ЭВМ.

В качестве недостатка можно отметить его относительную сложность.