Силовые линии электрического поля.

Поле вектора можно представить графически в виде линий тока вектора, или силовых линий. Силовые линии – кривые в пространстве, касательные к которым совпадают с направлением вектора напряженности поля в данной точке:

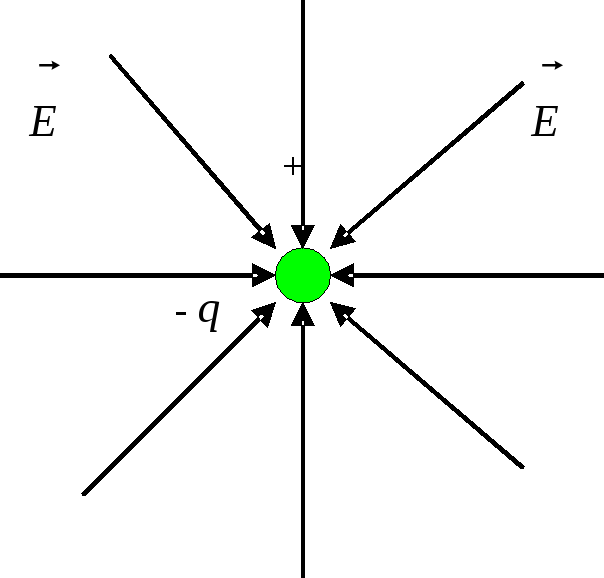
Рисунок 18.2. Силовые линии поля точечного положительного заряда	Рисунок 18..3. Силовые линии поля точечного отрицательного заряда

Густота силовых линий, т.е. число линий, пронизывающих единичную площадку, перпендикулярную линиям в данной точке, графически определяет модуль вектора напряженности электрического поля (пропорциональна модулю вектора ).

Рисунок 18..4. Силовые линии поля диполя	Рисунок 18..5. Силовые линии одно­родного электри­чес­кого поля

Теорема Гаусса.

Поток вектора через поверхность.

	Рассмотрим маленькую площадку с единичным вектором нормали: , в пределах которой вектор напряженности электрического поля имеет постоянное значение: . Для замкнутых поверхностей принято выбирать внешнюю нормаль,
Рисунок 18..6.

т.е. нормаль , направленную наружу охватываемой поверхностью области.

В этом случае элементарный поток вектора через площадкуопределяется как скалярное произведение вектора поля на вектор элементарной площадки:

(18.9)

Т.о., поток вектора есть скалярная величина.

Поток вектора через конечную поверхность равен:

(18.10)

Поток вектора через замкнутую поверхность.

Рисунок 18.7.

Рассмотрим для начала точечный заряд, окруженный сферической поверхностью с центром, совпадающим с точечным зарядом. Т.к. для любого элемента рассматриваемой поверхности , то

Для элемента произвольной замкнутой поверхности

,

(18.11)

где – телесный угол. Этот угол может принимать как

	положительные, так и отрицательные значения в зависимости от направления нормали (значения угла ), т.е. является величиной алгебраической. Из рисунка видно, что входящий и один из выходящих через поверхности, ограниченные телесным углом, потоков «компенсируют» друг друга, так что отличным от нуля остается только один выходящий в телесном углепоток.
Рисунок 18.8

Тогда полный поток вектора через произвольную замкнутую поверхность равен

(18.12)

Т.о., полученный результат не зависит ни от положения заряда внутри пространства, ограниченного поверхностью , ни от выбора самой поверхности.

	Теперь пусть поле создается любой системой зарядов. Тогда всю систему можно разбить на точечные заряды и для каждого из них в отдельности найти потоки через выбранную замкнутую поверхность. Пользуясь принципом суперпозиции, получим, что уравнение
Рисунок 18.9.

может быть обобщено для любой системы зарядов, расположенных произвольным образом, причем стоящий в правой части уравнения заряд будет складываться только из зарядов, находящихся внутри рассматриваемой замкнутой поверхности.

Т.о., получаем:

,

(18.13)

т.е. из геометрического правила сложения векторов следует, что их потоки, как и заряды, складываютсяалгебраически.

Итак, электростатическая теорема Гаусса:

.

(18.14)

где суммарный заряд внутри поверхности.

Поток вектора сквозь замкнутую поверхность равен с точностью до множителяалгебраической сумме зарядов внутри этой поверхности.

Для непрерывного распределения заряда с объемной плотностью , зависящей от координат, имеем

(18.15)

Применение теоремы Гаусса для расчета полей.

Рассмотрим практическое применение теоремы Гаусса для расчета электрических полей.

а) Поле бесконечной равномерно заряженной с поверхностной плотностью плоскости (Рисунок 18.10):

	Вектор напряженности поля бесконечной равномерно заря­жен­ной плоскости направлен перпендикулярно плоскости, что следует из симметрии рассматриваемой задачи, т.е.(нормаль к плос­кости) или(элемент поверхности плоскости). В качестве поверхности, которую мы
Рисунок 1810.

используем для расчета, выберем цилиндрическую поверхность (см. рисунок).

	Поскольку поле по обе стороны плоскости одинаково (Рисунок 18.11), а поток через боковую поверхность цилиндра равен нулю (из-за равенства нулю скалярного произведения и элемента боковой поверхности), получаем , или
Рисунок 1811.
		(18.16)

б) Поле бесконечного равномерно заряженного с линейной плотностью цилиндра (нити):

	Из соображений симметрии следует, что в рассматриваемом случае поле имеет радиальный характер, т.е. вектор в каждой точке перпендикулярен оси цилиндра, а модуль вектора напряженности зависит только от расстоянияот оси цилиндра. Поэтому в качестве вспомогательной замкнутой поверхности выбираем в форме коаксиального прямого цилиндра, как показано на рисунке 18.12
Рисунок 18.12.

По теореме Гаусса для случая получаем

откуда

, ().

(18.17)

Использование теоремы Гаусса для расчета полей эффективно лишь в случаях, где поле обладает специальной симметрией (чаще плоской, сферической, цилиндрической), чтобы можно было найти достаточно простую замкнутую поверхность, окружающую заряды и использовать простой способ вычисления потока вектора .

В тоже время теорема Гаусса имеет фундаментальное значение для теории. Она выражает тот факт, что электрические заряды, заключенные внутри замкнутой поверхности являются источниками (стоками) электростатического поля

При этом поток вектора напряженностии заряд, ограниченный замкнутой поверхностью, могут рассматриваться как суммарная алгебраическая мощность источников и стоков поля.

Представим теперь теорему Гаусса применительно к бесконечно малому объему, расширив её возможности как инструмента исследования электрического поля.