Сторонние силы. Электродвижущая сила. Напряжение.

Для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называ­ются источниками тока. Силы неэлектро­статического происхождения, действую­щие на заряды со стороны источников тока, называются сторонними.

Сторонние силы совершают работу по перемещению электрических зарядов. Фи­зическая величина, определяемая работой, совершаемой сторонними силами при пе­ремещении единичного положительного заряда, называется электродвижущей си­лой (э. д. с.) , действующей в цепи:

,

Напряжением U на участке 1—2 на­зывается физическая величина, определя­емая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении еди­ничного положительного заряда на дан­ном участке цепи

,

где - разность потенциалов на концах участка цепи.

Основные законы электрического тока.

Закон Ома для однородного участка цепи.

Создание и поддержание в веществе электрического поля является одним из основных способов возбуждения электрического тока. Как показывает опыт, для многих тел в широких пределах справедливо соотношение

,

или

.

где - разность потенциалов на концах проводника с сопротивлением .

Последнее выражение можно переписать в дифференциальном виде

,

откуда,

.

или

где - удельная проводимость или электропроводность, зависящая от физического состояния тела (температуры, давления и т.д.); величина, обратная электропроводности, называется удельным сопротивлением материала.

Полученное выражение носит название закон Ома в дифференциальной форме.

Закон Ома для неоднородного участка цепи

Мы рассматрели закон Ома для однородного участка цепи, т. е. тако­го, в котором не дей­ствуют сторонние силы. Теперь рассмот­рим неоднородный участок цепи, где дей­ствующую э.д.с. на участке 1—2 обозна­чим через , а приложенную на концах участка разность потенциалов — через .

.

Это выражение представ­ляет собой закон Ома для неоднородного участка цепи в интегральной форме, кото­рый является обобщенным законом Ома.

2. Закон Джоуля-Ленца.

Энергия, выделяемая при прохождении электрического тока на участке цепи, равна

В дифференциальной форме

Откуда

,

или

Уравнения () и () выражают закон Джоуля-Ленца, соответственно, в интегральной и дифференциальной формах.

Закон сохранения электрического заряда.

Одним из фундаментальных законов электричества является закон сохранения электрического заряда, установленный в результате обобщения опытных фактов. Придадим ему математическое выражение, связав с такими макроскопическими величинами, как плотность заряда и плотность электрического тока . Если вектор плотности тока с течением времени

	повсюду остается постоянным, то говорят, что мы имеем дело с системой стационарных токов. Стационарные токи удовлетворяют закону сохранения заряда. Возьмем в проводящей среде произвольную замкнутую поверхность , ограничивающую некоторый объем . Количество электричества, ежесекундно вытекающее из объема

через поверхность , выражается интегралом . С другой стороны убыль заряда в объеме можно представить в виде , где - заряд, содержащийся в объеме . Приравнивая эти выражения, получаем

.

Минус в правой части уравнения показывает, что происходит уменьшение полного заряда внутри объема . Представив заряд, находящийся в рассматриваемом объеме как

,

и воспользовавшись теоремой Гаусса-Остроградского

,

получаем

.

Поскольку это уравнение записано для произвольного объема, то равенство справедливо также и для подынтегральных выражений:

Это и есть уравнение непрерывности, или уравнение неразрывности, выражающее закон сохранения электрического заряда.

Если токи стационарны, тогда

, то

или

Знак частной производной используется в связи с тем, что , вообще говоря, зависит как от времени, так и от пространственных координат.
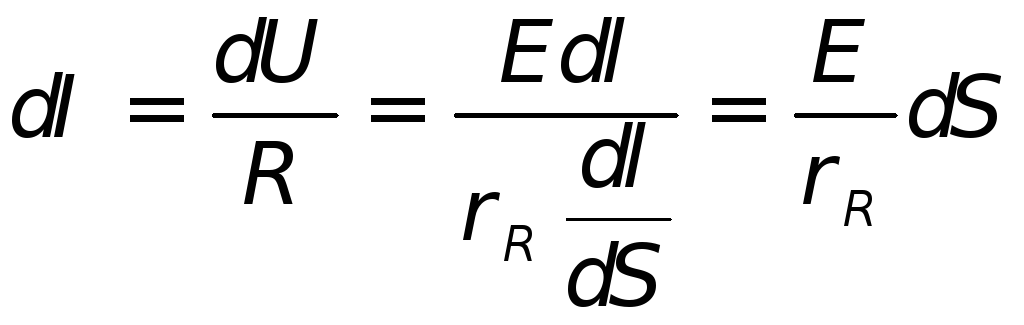