
Методичка по Маткаду
.pdf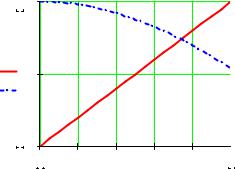
ЛАБОРАТОРНАЯ РАБОТА № 4
Тема: Решение уравнений и систем уравнений.
Цель: научиться решать квадратные уравнения, уравнения с одной производной, а также системы и нелинейных уравнений, используя возможности программы Mathcad.
ХОД РАБОТЫ
1. Простейший способ найти корень уравнения с одним неизвестным обеспечит функция root. Например, необходимо найти корень
трансцендентного уравнения x cos x . Зададим начальное значение x 1 ,
решение дается функцией root x cos x , x 0.74
Точность вычислений задаётся системной переменной TOL, равной по умолчанию 10 3 и определённой в меню Math Options.
Проиллюстрируем полученное решение.
TOL : 10 8 x : 1 x0 : root x cos x , x
x0 0.739
x : 0,0.05..1
1 |
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
cos(x) |
0.5 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
|
|||||
|
0 |
|
x |
|
1 |
Здесь мы явно изменили значение системной переменной TOL.
x0 – переменная с текстовым индексом, который вводится при помощи
точки: x.0. Текстовый индекс – это просто декоративное украшение, он является составной частью имени переменной.
Отметим ещё, что при выводе результата отображается только 3 значащих цифры после десятичной точки. Эту установку можно изменить в меню Format Number в переменной Displayed Precision.
Используя возможности программы Mathcad, можно найти корни
уравнения f x 0 |
для заданной функции f x . |
31

2
Определим функцию: f x : 3 e 3x 3 x3 ex .
Зададим начальное приближение для поиска корня x : 1. Если уравнение имеет несколько корней, для поиска нового корня следует задавать новое начальное приближение. Для поиска комплексных корней следует задавать комплексное начальное приближение. Получаем искомое решение:
sol : root f x , x ; |
sol 0.773 . Иногда алгоритм поиска корня |
натыкается на локальный минимум функции, при этом появляется сообщение “отсутствие сходимости” (испытайте на данном примере начальное приближение х=10). В таком случае следует попробовать другое начальное решение.
2. Программа Mathcad позволяет находить корни многочлена любой
степени f x an xn |
an 1xn 1 an 2 xn 2 a1x a0 . |
|
|
|||||
Рассмотрим на примере решения квадратного уравнения. Введем |
||||||||
коэффициенты |
a : 1 |
b : 2 |
c : 8. |
И |
определим |
функцию: |
||
f x : ax2 bx c . |
Переменной |
v присваиваем |
значение: |
v : cba T . |
||||
Переменной |
r |
присвоим |
значение |
функции |
polyroots v : |
|||
2 r : polyroots v . Получаем корни: r .
4
3.Поиск корней при помощи блока Given .........Find(...)
x: 1
y: 1
Здесь могут решаться уже системы уравнений с несколькими неизвестными, однако, как и в предыдущем случае, необходимо задание начальной точки от которой будет происходить поиск решения. Решение ищется методом итераций и при наличии нескольких корней, очевидно, будет найдено лишь ближайшее решение, если оно существует.
Given
x3 sin( y)  25 y2 cos(x) 27
25 y2 cos(x) 27
x
Find (x y)
y
x 2.96 |
y 5.101 |
Используя блок решения уравнений, Mathcad находит решение системы n нелинейных уравнений с n неизвестными.
32
Зададим начальные приближения для всех неизвестных: x : 1 y : 1
z : 0 .
Вводим уравнения в блок решения уравнений:
Given (начало блока–дано)
2 x y 5 2 z2
y3 4 z 4
x y z ez
vec : find x, y, z (конец блока–найти)
Найденное решение:
|
1.422 |
||
vec |
|
0.975 |
|
|
|
||
|
|
0.768 |
|
|
|
|
|
Таким же образом можно решать и системы линейных уравнений, однако приходится задавать начальную итерацию, потому системы линейных уравнений лучше решать матричным методом.
4. Поиск решения при помощи блока Given .........Minerr(...).
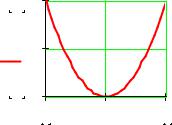
Практически то же, что и в предыдущем случае, однако здесь решение будет найдено в любом случае, даже при его отсутствии. Дело в том, что здесь ищется не решение системы, а минимальная невязка уравнений. Рассмотрим функцию, заведомо не имеющую действительных корней и найдем точку, в которой эта функция наиболее приближена к оси Ох.
При построении графика необходимо указать начальное значение
y : 0 |
|
|
|
y x : x2 |
2x 1.5 |
|
|
x : 0,0.05..2 |
|
||
1.5 |
1.5 |
|
|
y(x) |
1 |
|
|
0.5 |
0.5 |
1 |
2 |
|
0 |
||
|
0 |
x |
2 |
Для этого простого случая очевидно, что наименьшая невязка функции будет при x=1.
33
x 0 Given
y(x)  0
0
Minerr(x) 1
Первая строка даёт нам решение х=1, а системная переменная ERR показывает невязку уравнения.
ERR 0.5
Аналогично решаются и более сложные уравнения или их системы.
5. Решим матричным способом систему линейных уравнений:
0.3w 0.2x 6.6y 1.1z 1
4.5w 1.8x 0.3y 6.5z 0.1
7.3w 9.7x 10.9y 4.4z 0.01
8.1w 2.7x 8.7 y 8.9z 0.001
Запишем систему в матричном виде: |
AB X , где |
|
|||||||||||
0.3 |
0.2 |
6.6 |
1.1 |
|
|
|
1 |
|
|
||||
4.5 |
1.8 |
0.3 |
6.5 |
B |
|
|
0.1 |
|
|
||||
A 7.3 |
9.7 |
10.9 |
4.4 |
и |
|
0.01 |
|
|
|||||
|
8.1 |
2.7 |
8.7 |
8.9 |
|
|
|
|
|
|
|
||
|
|
|
|
0.001 |
|
||||||||
Решением |
этой |
системы |
будет |
вектор |
X x1 x2 |
x3 , который |
|||||||
находим по формуле: |
X : A 1 |
B |
|
|
|
|
|
|
|||||
Результат можно вывести двумя способами: |
|
||||||||||||
а) в виде матрицы: |
|
|
|
|
|
|
|
|
|
||||
x1 |
|
|
|
|
|
3.937 |
|
|
|||||
x |
|
|
|
|
|
|
|
||||||
X |
2 |
|
в нашем случае X 2.975 |
|
|
||||||||
x |
|
|
|
|
|
|
0.746 |
|
|
|
|||
|
3 |
|
|
|
|
|
|
1.952 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
б) в виде отдельных элементов:
В этом случае доступ к элементу матрицы производится по индексу, отсчитывая от 0. Вектор-столбец имеет один индекс, который вводится при помощи символа левой квадратной скобки – [. Например, решение рассмотренной выше задачи можно вывести так:
x0 3.937 x1 |
2.975 x2 |
0.746 |
x3 1.952 |
Вводится x[0пробел |
x[1пробел |
x[2пробел |
|
34
Двумерный массив имеет уже два индекса, также отсчитываемые от 0,
первый из них нумерует строки, второй – столбцы. Так, для матрицы А, это
будет выглядеть так: |
A0,0 1 |
A0,2 0 |
A2,2 5 |
A2,0 1 |
Вводим A[0,0= |
A[0,2= |
A[2,2= |
A[2,0=. |
Индексы разделяются |
запятыми. |
|
|
|
|
6. Для решения систем линейных уравнений можно использовать и встроенную функцию lsolve(...).
Пусть задана система линейных уравнений:
2x 3y 1
x 5y 0
Матрицы коэффициентов:
|
2 |
3 |
A |
|
|
1 5
1
B |
|
0
а) Система может быть представлена как A X B , её решение:
0.385
lsolve A, B 0.077
Ищем решение матричным способом:
X : A 1 B
0.385
X 0.077
б) Решим эту же систему при помощи блока Given ... Find(...)
x : 0 |
y : 0 |
Given
2 x 3 y  1
1
x 5 y  0
0
X Find(x y)
|
0.385 |
X |
|
0.077
7.Решение уравнений в символьном виде.
Некоторые уравнения Mathcad может разрешить в символьном виде. Для этого существуют три возможности:
первая – это использование меню Symbolics,
35
вторая – использование оператора solve, x
третья – использование блока Given .... Find(...) .
Например, запишем квадратный трёхчлен, выделим переменную x и выберем в меню пункт Symbolics Variable Solve. Получим решение в символьном виде.
Для того, чтобы решение было записано справа от выражения,
необходимо установить |
флажок |
|
|
|
|
в меню Symbolics Evaluation |
|||||||||
Style Horizontally |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|||
a x b x c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
b |
|
c |
|
|
||||||||
|
2 a |
b |
|
|
4 a |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
b b |
|
4 a c |
|
|
|
|
|||||
|
|
|
|
|
|||||||||||
|
|
2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
При использовании оператора необходимо иметь в виду, что переменные не должны быть определены заранее; так попытка раскрытия квадратного уравнения
a x2 b x c solve x приведёт к ошибке однако, квадратный трёхчлен
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
||
|
|
|
|
|
|
b |
|
|||||||||||
|
|
|
|
|
b |
|
|
|
4 a |
c |
||||||||
2 |
b z c solve z |
|
2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a z |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
||
|
|
|
|
|
|
b |
c |
|||||||||||
|
|
|
|
|
b |
|
|
|
4 a |
|
|
|
|
|
||||
|
|
|
2 a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
раскрывается вполне удовлетворительно.
Попробуем теперь решить систему линейных уравнений.
Given
u 2 v |
|
a |
|
|
|
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
4 u v |
|
|
b |
|
2 b a |
||||
|
|
||||||||
|
|||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Find (u v) |
1 8 |
|
|||||||
|
4 a b |
|
|||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 8
Вданном случае, нам пришлось вводить неиспользованные до сих пор переменные u v, поскольку переменные x и y уже определены. Обойти эти
36
трудности можно довольно просто, если решить уравнение на новом рабочем листе.
Покажем ещё решение для полинома третьего порядка. a : 1 b : 1 c : 1 d : 1
|
|
|
|
|
1 |
|
3 |
2 |
|
|
|
|
|
a z |
b z |
c z d solve z |
|
|
i |
|
i
Мы определили заранее значение констант, в противном случае решение получится в общем виде и на лист не помещается. Попробуйте его вывести и посмотрите, что получится.
8. Выполните индивидуальное задание, показать результат преподавателю и оформить отчет по лабораторной работы.
ВАРИАНТЫ ЗАДАНИЙ
Задание для всех вариантов.
1. Решить систему линейных уравнений матричным способом.
|
|
|
|
|
|
|
|
|
x 5x x V 12 |
|||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
3x1 x2 x3 V 1 |
|||||
|
|
|
|
|
|
|
|
|
|
3x2 |
V 4 x3 V V 2 6 |
|||
|
|
|
|
|
|
|
|
|
Vx1 |
|||||
|
Здесь V – номер варианта. |
|
||||||||||||
2. Решить уравнение с одной неизвестной. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
№ |
Трансцендентное |
|
|
Алгебраическое уравнение |
||||||||||
вар. |
|
|
уравнение |
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
||||
1. |
x |
|
|
|
|
|
|
|
0 |
|
|
|
x4 4x3 10x2 3x 4 0 |
|
3 sin 3,6x |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
x |
sin x |
1 0 |
|
|
|
|
x5 5x2 4,5 0 |
||||||
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
3. |
0,4 arctg |
|
x 0 |
|
|
x5 x 0,2 0 |
||||||||
x |
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||
4. |
3sin |
|
5x 3,8 0 |
|
|
x3 0,2x2 0,5x 1,5 0 |
||||||||
x |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||
|
1 x sin x ln |
1 x |
|
0 |
|
10 |
||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
x |
1 0 |
|||
6. |
ln x 1,8 x 0 |
|
|
|
x8 2x 1,5 0 |
|||||||||
|
|
|
|
|
|
|
||||||||
7. |
x sin x 8 0 |
|
|
|
|
x4 2x2 8x 1 0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |

8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 4x2 5x 2 0 |
||
arccos x |
|
|
1 0,3x2 |
0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
1 |
|
|
|
|
|
|
x 0 |
|
6x8 2x2 3 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 sin 3,6x |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10. |
1 |
sin x |
x 0 |
|
3,5x5 2,8x3 7,5x 2,5 0 |
|||||||||||
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
11. |
|
x arctg |
|
|
|
|
0,4 0 |
x5 x4 x3 |
x2 1 0 |
|||||||
|
|
x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
12. |
|
|
|
|
|
|
|
|
1,5x5 17x 21 0 |
|||||||
|
1 0,3x2 |
|
arccos x 0 |
|||||||||||||
|
|
|
|
|
|
|
||||||||||
13. |
ln 4 2x x2 2 0 |
2x4 3,5x2 |
3 0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
14. |
e 6 x 3x2 |
18 0 |
|
17x9 15x7 |
13x5 11x3 9x 7 0 |
|||||||||||
15. |
|
2x 4x 0 |
|
x4 |
2x3 1 0 |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
16. |
ln x x 1 3 0 |
|
x5 |
21x2 55 0 |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||
17. |
arctg x 2 x 0 |
|
x7 |
2x6 3x5 4x4 5x3 6x2 7x 8 0 |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||
18. |
|
x2 4sin x 2 0 |
|
8x7 7x6 6x5 5x4 4x3 3x2 2x 1 0 |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
19. |
|
x ln 7 4x 0 |
|
x50 1 0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
20. |
e 2x |
3 |
1 0 |
|
x7 |
6x6 x5 4x4 x3 2x2 x 1 0 |
||||||||||
|
|
|||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Решить уравнение в символьном виде.
1.x3 a 0
2.x5 b a x4 abx3 ax2 ax b a a2b 0
3.x5 bx4 a4 x a4b 0
4.x4 2x3 1 a x2 4a 1 2x 1 a 4a 0
5.x5 3x4 a b3 x3 3 b3 a x2 ab3 x 3ab3 0
6.x5 ax3 2x2 2a 0
38
7.x7 ax5 x2 a 0
8.2x 2 a b 0
9.ln sin x 2a 0
10.e 2 x 2a 0
11.sin ax cos ax 0
12.sin ax tgax 0
13.e ax eax 0
14.e ax eax 1 0
15.e ax eax ln a 0
16.ae x bex 0
17.a sin x b cos x 0
18.x5 a 0
19.x6 ax4 x a 0
20.3x 5 a b 0
39
ЛАБОРАТОРНАЯ РАБОТА № 5
Тема: Вычисление сумм и произведений. Символьные вычисления. Операции с комплексными числами
Цель: Научиться вычислять суммы и произведения элементов множеств в цифровом и символьном виде, выполнять операции с комплексными числами.
ХОД РАБОТЫ
1. Для вычисления сумм и произведений воспользуемся панелью Матанализ
 на панели инструментов математика.
на панели инструментов математика.
Например: вычислим суммы следующих рядов:
100 1 |
|
20 |
1 |
n |
|
|||
1.635 |
|
|
|
1.543 |
||||
|
|
|
||||||
|
|
|
|
|
||||
n 1 n2 |
2n ! |
|||||||
|
n 0 |
|
||||||
1000 |
1 |
|
|
|
0.5 |
||
|
|||
k 1 |
2k 1 2k 1 |
||
Здесь мы использовали значок суммы  с указанием границ суммирования. Из примеров видно, что система обрабатывает ситуации
с указанием границ суммирования. Из примеров видно, что система обрабатывает ситуации
1 0 1 и |
0! 1. Но, к сожалению, не может считать суммы с |
бесконечными пределами. В случаях, когда пределы изменения индекса указываются в виде переменной интервального типа (например, для работы с матрицами и функциями, зависящими от индекса) используется знак
суммирования только с указанием индекса 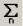 .
.
|
|
|
|
|
|
|
|
0.282 |
|||||
Например: 1) вычислим сумму элементов матрицы: X |
|
|
0.359 |
|
|||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
0.513 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
0.282 |
|
|
|
|
|
|
|
|
|
|
||
X : |
|
0.359 |
|
|
i : 0..2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0.513 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xi |
1.154 |
|
|
|
|
|
|
|
|
|
|
||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) n : 1..100 |
|
y n : n |
2 |
2n 1 |
|
n |
|
1 |
|
|
0.635 |
||
|
|
|
y n |
|
|||||||||
|
|
|
|
|
|
5 |
|
8 |
1 |
|
|||
2. Аналогично вычисляются произведения. a |
|
5 |
|
4 |
2 |
|
|
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
5 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
