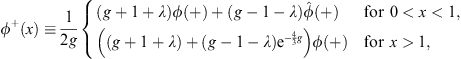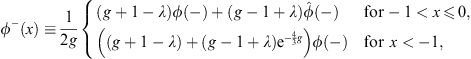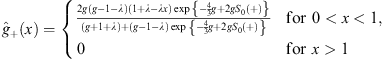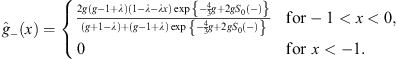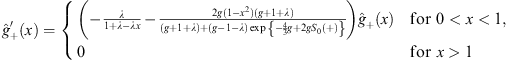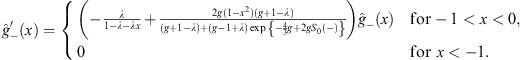4. Asymmetric quartic double-well problem

The hierarchy theorem established in the previous section has two restrictions: (i) the limitation of half-space x  0 and (ii) the requirement of a monotonically decreasing perturbative potential w (x). In this section, we shall remove these two restrictions.

Consider the specific example of an asymmetric quadratic double-well potential

(4.1)

with the constant λ > 0. The ground state wave function ψ (x) and energy E satisfy the Schroedinger equation

(T+V(x))ψ(x)=Eψ(x),

(4.2)

where , as before. In the following, we shall present our method in two steps: We first construct a trial function  (x) of the form

(4.3)

At x = 0,  (x) and ′ (x) are both continuous, given by

(0)=+(0)=-(0)

(4.4)

and

′(0)=+′(0)=-′(0)=0,

(4.5)

with prime denoting , as before. As we shall see, for x > 0, the trial function  (x) = ⁺ (x) satisfies

(4.6a)

with

(4.7a)

whereas for x < 0,  (x) = ⁻ (x) satisfies

(4.6b)

with

(4.7b)

Furthermore, at x = ±∞

v+(∞)=v-(-∞)=0.

(4.8)

Starting separately from ⁺ (x) and ⁻ (x) and applying the hierarchy theorem, as we shall show, we can construct from  (x) another trial function

(4.9)

with χ (x) and χ′ (x) both continuous at x = 0, given by

χ(0)=χ+(0)=χ-(0)

(4.10)

and

χ′(0)=χ+′(0)=χ-′(0)=0.

(4.11)

In addition, they satisfy the following Schroedinger equations

(4.12)

and

(4.13)

From V (x) given by (4.1) with λ positive, we see that at any x > 0, V (x) > V (−x); therefore, E⁺ > E⁻.

Our second step is to regard χ (x) as a new trial function, which satisfies

(T+V(x)+w(x))χ(x)=E0χ(x)

(4.14)

with w (x) being a step function,

(4.15)

and

(4.16)

We see that w (x) is now monotonic, with

w′(x)0

(4.17)

for the entire range of x from −∞ to +∞. The hierarchy theorem can be applied again, and that will lead from χ (x) to ψ (x), as we shall see.

4.1. Construction of the first trial function

We consider first the positive x region. Following Section 2.1, we begin with the usual perturbative power series expansion for

ψ(x)=e-gS(x)

(4.18)

with

gS(x)=gS0(+)+S1(+)+g-1S2(+)+

(4.19)

and

E=gE0(+)+E1(+)+g-1E2(+)+

(4.20)

in which S_n (+) and E_n (+) are g-independent. Substituting Figs. (4.18), (4.19) and (4.20) into the Schroedinger equation (4.2) and equating both sides, we find

(4.21)

(4.22)

etc. Thus, (4.21) leads to

(4.23)

Since the left side of (4.22) vanishes at x = 1, so is the right side; hence, we determine

E0(+)=1+λ,

(4.24)

which leads to

S1(+)=(1+λ)ln(1+x).

(4.25)

Of course, the power series expansion Figs. (4.19) and (4.20) are both divergent. However, if we retain the first two terms in (4.19), the function

(4.26)

serves as a reasonable approximation of ψ (x) for x > 0, except when x is near zero. By differentiating  (+), we find  (+) satisfies

(T+V(x)+u+(x))(+)=gE0(+)(+)

(4.27)

where

(4.28)

In order to construct the trial function  (x) that satisfies the boundary condition (4.5), we introduce for x  0,

(4.29)

and

(4.30)

so that ⁺ (x) and its derivative ⁺′ (x) are both continuous at x = 1, and in addition, at x = 0 we have ⁺′ (0) = 0. For x 0, we observe thatV (x) is invariant under

(4.31)

The same transformation converts ⁺ (x) for x positive to ⁻ (x) for x negative. Define

(4.32)

where

(4.33)

(4.34)

and

(4.35)

Both ⁻ (x) and its derivative ⁻′ (x) are continuous at x = −1; furthermore, ⁺ (x) and ⁻ (x) also satisfy the continuity condition Figs. (4.4) and (4.5), as well as the Schroedinger equation Figs. (4.6a) and (4.6b), with the perturbative potentials v₊ (x) and v_- (x) given by

(4.36a)

and

(4.36b)

in which u₊ (x) is given by (4.28),

(4.37)

(4.38a)

and

(4.38b)

In order that u₊ (x), be positive for x > 0 and u_- (x), positive for x < 0, we impose

(4.39)

in addition to the earlier condition λ > 0. From Figs. (4.28) and (4.37), we have

(4.40a)

and

(4.40b)

Likewise, from Figs. (4.38a) and (4.38b), we find

(4.41a)

and

(4.41b)

Furthermore, as x → ±1,

(4.42a)

and

(4.42b)

Thus, for x 0, we have

(4.43)

and, together with Figs. (4.36a) and (4.40a),

(4.44a)

for x positive. On the other hand for x  0, is not always positive; e.g., at x = 0,

which is positive for , but at x = −1+,

However, at x = −1, . It is easy to see that the sum can satisfy for x  0,

(4.44b)

To summarize: ⁺ (x) and ⁻ (x) satisfy the Schroedinger equation Figs. (4.6a) and (4.6b), with v_± (x) given by Figs. (4.36a) and (4.36b),

(4.45a)

and

(4.45b)

and the boundary conditions Figs. (4.4) and (4.5). In addition, v_± (x) satisfies

(4.46)

and the monotonicity conditions Figs. (4.7a) and (4.7b).