
1 СЕМЕСТР. Экономика. Микроэкономика. Поведение, институты и эволюция Самуэль Боулз / Микроэкономика. Поведение, институты и эволюция_Самуэль Боулз_2010 -576с
.pdf
Глава 4. Провалы координации и институциональные изменения 129
можем записать функцию полезности Нижнего как функцию уровня усилий его и Верхнего
v = v (e, E), V = V (e, E).
Представленные в пространстве (e, E) на рис. 4.2 функции описывают уже знакомые нам кривые безразличия (показаны только для Нижнего). Полагая
dv = vede + vEdE = 0,
мы видим, что
dE = − ve . de vE
Следовательно, нам известно, что наклоны кривых безразличия (для Ниж него) равны −ve/vE и аналогично равны для Верхнего. Предполагаемый экспе римент, задающий функцию наилучшего ответа, состоит в том, чтобы зафик сировать некоторое время ловли Верхнего и узнать, как долго станет рыбачить Нижний в этих обстоятельствах. Мы изобразили это на рис. 4.2, нарисовав го ризонтальную пунктирную линию E (произвольно выбранный уровень усилий Верхнего) как ограничение и предлагая ему максимизировать свою полезность, находя точку, в которой касаются его наивысшая возможная кривая безразли чия и ограничение. Наклон ограничения равен 0, поэтому для оптимума необхо димо, чтобы наклон кривой безразличия Нижнего также равнялся 0, что требует ve = 0, как мы и видели ранее.
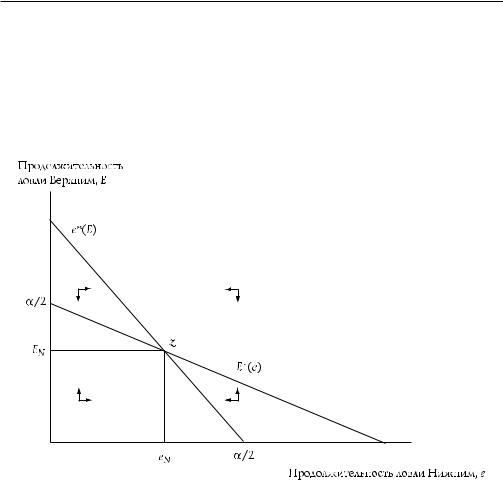
Рис. 4.2. Функция реакции Нижнего, e*(E)

130Часть I. Координация и конфликт: базовые социальные взаимодействия
Язаписываю функцию наилучшего ответа Нижнего как e*=e*(E), звездочкой обозначая решение задачи на поиск оптимума. e*(E) представлено на рис. 4.2
множеством точек, для которого ve = 0 и в которых у Нижнего не будет стимула изменить свои действия. Мы знаем, что равновесие по Нэшу должно быть вза имным наилучшим ответом. Значение равновесного по Нэшу e таким образом
может быть подсчитано подстановкой функции наилучшего ответа Верхнего в функцию наилучшего ответа Нижнего и затем решением по e, как и показано на рис. 4.3. Изза (предполагаемой) симметричности задачи получаем как для Верхнего, так и для Нижнего
eN = |
|
|
α |
= EN . |
(4.8) |
|
2 |
+ αβ |
|||||
|
|
|
||||
О чем говорят полученные величины? Без знания институциональной струк туры взаимодействия между рыбаками мы не имеем возможности сказать, ка кими станут их уловы: эти значения равновесия по Нэшу могут не соответство вать действительности, если, например, один из игроков ходит первым. Однако такой исход способен стать достаточно маловероятным еще и по более простой причине: равновесие по Нэшу может быть неустойчивым.
Неравновесная динамика и устойчивость. Для устойчивости требуется, чтобы даже маленькие колебания равновесных значений были самокорректи рующимися. Чтобы в этом убедиться, нам необходимо знать коечто о поведе нии рыбаков вне равновесия: что они делают, когда они не находятся в точке равновесия по Нэшу? Стоит посмотреть на топографическую карту с e*=e*(E), описывающей вершину горы. Процесс оптимизации Нижнего — это алгоритм подъема в гору: для e ≠ e* условия первого порядка для Нижнего не выполнены, и для e < e* на рис. 4.1 мы можем увидеть, что (1 - βE) > 2e, или предельная выгода от ловли превышает предельные затраты (дисполезность) ловли, так что Нижний решит рыбачить больше.
Динамика системы вне равновесия устроена следующим образом: в соот ветствии с тем, что люди имеют ограниченные когнитивные возможности, мы предполагаем, что рыбаки используют эмпирическое правило — в конце пери ода изменить свое поведение в направлении, оптимальном в условиях того, как другой индивид поступал в данном периоде. Подобный шаг недальновиден в обоих направлениях: рыбак оглядывается назад только на один период (исполь зуя данные конкретного периода, чтобы определить, как поступать в следую щем), и совсем не смотрит в будущее (предполагая, что действия других игроков не изменятся между данным периодом и следующим). Это приводит к такому правилу: в следующем периоде двигаться в направлении действий, оптимальных в этом периоде. При e′ и E′ — действиях рыбаков в следующем периоде — это эмпирическое правило опытного пути задает
De ≡ e′ - e = γ (e* - e), DE ≡ E ′ - E = G (E* - E),
где γ и G — положительные дроби [0, 1], отражающие скорость приспособ ления (какая часть разрыва между желаемым и действительным уровнем ловли
Глава 4. Провалы координации и институциональные изменения 131
в этом периоде закрыта выбором уровня ловли в следующем периоде). Конечно, скорость приспособления для двух рыбаков отличается (Нижний может быть
человеком привычки с γ, близкой к 0, а Верхний молниеносно реагировать, как Homo economicus с G = 1). Динамика системы, выраженная данными уравнения
ми, говорит о том, что каждый движется в сторону своей функции наилучшего ответа, обозначенного стрелками на рис. 4.3.
Рис. 4.3. Динамика вне равновесия и устойчивое равновесие по Нэшу
Примечание. Стрелки обозначают ответ на неравновесие двух рыбаков (движение по горизонтали для Нижнего, по вертикали — для Верхнего). Точка z — равновесие по Нэшу.
Возможно, вы удивитесь, но движения каждого рыбака в сторону своей функции наилучшего ответа недостаточно для того, чтобы гарантировать устой чивость равновесного по Нэшу исхода, определяемого их пересечением. Чтобы понять, почему это так, предположим, что функции наилучшего ответа таковы, что если Верхний рыбачит на один час больше, то Нижний рыбачит меньше на два часа, т. е. de*/dE = -2, и наоборот; и представим, что время ловли обоих в текущем периоде есть равновесная по Нэшу величина. На рис. 4.4 представлена внеравновесная динамика: равновесие по Нэшу является седловой точкой, а ко лебания не самокорректирующиеся.
Становится ли равновесие по Нэшу асимптотически устойчивым, зависит от относительных наклонов функций наилучшего ответа. Чтобы равновесные по Нэшу величины были устойчивы, необходимо, чтобы ни один из рыбаков не от вечал за другого; т. е. на рис. 4.3 функция E*(e) должна быть более «пологой», чем
132 Часть I. Координация и конфликт: базовые социальные взаимодействия
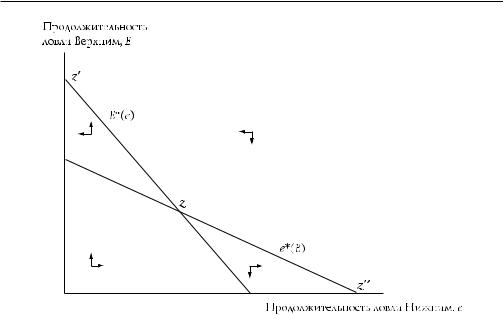
Рис. 4.4. Неустойчивое равновесие по Нэшу (z)
Примечание. Существуют также два устойчивых равновесия по Нэшу (z ′ и z ′′).
функция e*(E). Применяя функцию наилучшего ответа, определенную выше, по лучаем, что для выполнения этого требуется:
αβ |
< |
2 |
, |
(4.9) |
|
2 |
αβ |
||||
|
|
|
т. е. необходимо, чтобы αβ < 2, из чего следует, что влияние изменений в ловле Верхнего на Нижнего, de*/dE, было бы меньше 1 по абсолютной величине. Вы ражение становится более сложным, когда α и β отличаются для двух рыбаков, но рассуждение остается прежним: для устойчивости требуется, чтобы игроки не переигрывали.
Устойчивость можно рассматривать как необходимое, но недостаточное условие для того, чтобы равновесие по Нэшу можно было считать хорошим про гнозом реального поведения. Первая причина, подтверждающая это, знакома: как нам известно из гл. 2, может существовать множество устойчивых равно весий по Нэшу, как на рис. 4.4. Вторая причина не столь очевидна: реалистич ные правила, по которым индивиды адаптируют свое поведение в соответствии с прошлым опытом, возможно, не смогут привести игроков к равновесию по Нэшу, даже если оно единственно и устойчиво. При очень сложных взаимодей ствиях индивиды могут не суметь «научиться» приходить к равновесию по Нэшу в игре. Но даже в, казалось бы, простой игре — например, «камень, ножницы, бу
мага» — ни реальные люди, ни компьютер даже после сотен раундов игры обыч но не выбирают стратегии, являющиеся равновесием по Нэшу (Sato, Akiyame &
Farmer, 2002). В игре «камень, ножницы, бумага» существует только одно равно весие по Нэшу в смешанных стратегиях (когда каждый выбирает стратегию

Глава 4. Провалы координации и институциональные изменения 133
случайно с вероятностью 1 : 3), но мало кто играет так. В игры с единственным равновесием по Нэшу в чистых стратегиях гораздо проще играть, даже если их структура гораздо запутаннее, чем в игре «камень, ножницы, бумага».
Худшие по Парето исходы. Является ли равновесие по Нэшу Паретооп тимальным? Мы знаем, что для этого необходимо касание кривых безразличия двух рыбаков
ve = Ve . vE VE
Уравнение определяет кривую эффективных контрактов, точнее, множе ство всех Паретоэффективных пар часов ловли обоих рыбаков. Мы знаем, что для любого распределения, в котором оба рыбачат и кривые безразличия не касаются, — т. е. пересекаются — существует другое распределение, более вы годное для них обоих. Но равновесие по Нэшу — это точка на обеих кривых наилучшего ответа, определяемая соответственно равенствами ve = 0 и VE = 0. В равновесии по Нэшу две кривые безразличия не могут касаться; точнее, они перпендикулярны друг другу. Таким образом, в данном случае равновесие по Нэшу не является Паретооптимальным. Две точки на кривой эффективных контрактов p и ω обозначены на рис. 4.5.
Рис. 4.5. Равновесие по Нэшу: устойчивость и неоптимальность
Чтобы понять, почему равновесие по Нэшу хуже по Парето, представим, что двое игроков согласятся рыбачить на произвольно малое количество часов

134 Часть I. Координация и конфликт: базовые социальные взаимодействия
меньше. Как это повлияет на их благосостояние? Мы знаем, что Ve < 0 и vE < 0 (потому что ловля одного затрагивает другого, на что указывает β в их произ водственных функциях). Таким образом, при de < 0 и dE < 0, что обозначает их гипотетическое соглашение рыбачить чуть меньше, нам необходимо оценить изменение в полезности каждого
dv = deve + dEvE, |
|
dV = deVe + dEVE. |
(4.10) |
Заметим, что ve = 0 и VE = 0, потому что оба равенства определяют функции наилучшего ответа, а равновесие по Нэшу есть взаимный наилучший ответ. Сле довательно, оба выражения положительны: полезность каждого увеличится от
согласия рыбачить меньше. Отметим основную идею: каждый хотел бы, чтобы другой рыбачил меньше, и (что важно), поскольку они оба установили объем ловли на оптимальном уровне, они не думают о (бесконечно малом) сокращении собственной ловли. Линза, образованная двумя кривыми безразличия на
рис. 4.5, содержит Паретоулучшения по отношению к равновесию по Нэшу, z. Если к сделке можно принудить, тогда ее можно осуществить. Но как прий
ти к такому соглашению и как к нему принудить?
Предотвращение «трагедии рыбаков»
«Трагедия рыбаков» иллюстрирует характерный источник провалов координа ции: при заданных предпочтениях, соответствующих рассматриваемому случаю прав собственности и других аспектов стимулов, определяющих их решения, негативное влияние их ловли друг на друга (vE и Ve соответственно) не было ча стью процесса оптимизации каждого. Конечно, при предполагаемых правилах игры (неповторяющееся некооперативное взаимодействие) и предпочтениях (эгоистичных) сложно понять, как бы им удалось предотвратить трагедию. Но, как и ловцы лобстеров в Южной Австралии, некоторые реальные рыбаки очень хорошо управляют своими общими ресурсами. Когда индивиды кооперируют ся, чтобы поддерживать общину, это обычно происходит, потому что они суме ли превратить трагедию общин в другую игру, или их предпочтения не были полностью эгоистичными, или все вместе. Именно в такой момент появляются институты.
Хардин (Hardin, 1968) полагал, что «свобода общинных владений разрушает все» (С. 1244), и в результате он выступал за «взаимное принуждение, взаимно согласованное» (С. 1247). В своем гоббсовском пессимизме он не учел многие
непринудительные методы, посредством которых локальным сообществам уда лось предотвратить трагедию (Ostrom, Burger, Field, Norgaard & Policansky, 1999).
Подходы включают более удачное определение и меньшие препятствия к об мену правами собственности, взаимный мониторинг, соблюдение коллективных
выгодных общественных норм и многое другое. Три основных подхода к регу лированию общин можно обозначить так: приватизация общин, регулирование
общин государством или третьей стороной или регулирование посредством локальных взаимодействий между рыбаками. Три этих подхода иногда упоми

Глава 4. Провалы координации и институциональные изменения 135
нают как рынки, государство и сообщество соответственно (Ostrom, 1990; Ouchi, 1980; Taylor, 1997; Bowles & Gintis, 2002b). Поможет ли каждый из этих подходов
предотвратить или ослабить трагедию, зависит от того, как в подходах учитыва ется доступная информация, связанная с задачей, и как на это влияет ее исполь зование соответствующими игроками. Это также зависит и от особых возможно стей соответствующих институтов — государства, рынков и сообществ — влиять на поведение. Поскольку в большинстве наблюдаемых на практике (например, упомянутых выше) подходов будут прагматично скомбинированы элементы всех трех, я введу их отдельно, чтобы описать их свойства подробнее.
Следующие модели заметно упростят реальные институты, к которым ло кальные сообщества обращаются за решением перечисленных проблем и других провалов координации. Поражает разнообразие и сложность задействованных институтов. Например, Остром (Ostrom, 1999) и ее коллеги по области исследо вания обнаружили 27 различных локальных правил исключения других людей от доступа к ресурсам, от общего пользования. Ученые основывались на таких аспектах, как место жительства, возраст, каста, клан, уровень образования, про должительность пользования ресурсом, использование определенной техноло гии и т. д. Поскольку правила исключения часто использовались в комбинации, число определений институциональных ограничений значительно превысило 27. Правила, управляющие доступом к ресурсу для тех, кто не был исключен, также различались (как и упомянутые во введении правила конкурентного распреде ления, предложенные рыбаками северозападного побережья,). Наблюдаемые правила управления членством, размещением и другими аспектами управления общинами, в комбинации дают буквально тысячи гипотетических институтов управления общинами. Сотни из них наблюдаются на практике.
Приватизация. Предположим, один из рыбаков, например Нижний, владел бы озером и как владелец мог бы исключить Верхнего из ловли или регулировать время ловли Верхнего. В данном случае Нижний будет максимизировать свою полезность посредством изменения e и E. Предположим, что выбор Верхнего таков, что его полезность равна 0 при следующей наилучшей альтернативе. Оче видным ограничением в задаче оптимизации для Нижнего станет такое условие, что если Верхний вообще займется ловлей, то он должен получить не меньше,
чем в случае своей следующей наилучшей альтернативы. Данное ограничение назовем ограничением участия Верхнего (если оно нарушено, мы предполагаем,
что Верхний не участвует; если оно выполнено даже слабо (как равенство), мы предполагаем, что Верхний участвует). Ниже я рассмотрю, почему для Нижнего будет не оптимально отстранить Верхнего от ловли полностью.
Два типа взаимодействия между рыбаками могут иметь место в условиях приватизации. Нижний может выдать разрешение, при котором Верхний про должит ловить рыбу независимо, но вылавливать не более заданного количества рыбы, которое понадобится Верхнему, чтобы заплатить за разрешение сумму, не нарушающую ограничение участия. В другом случае Нижний может пред ложить Верхнему контракт найма, при котором Верхний станет рыбачить под надзором Нижнего, и рыба, пойманная Верхним, будет собственностью Ниж него. При этом компенсацией для Верхнего станет зарплата (выплачиваемая

136 Часть I. Координация и конфликт: базовые социальные взаимодействия
рыбой, пойманной обоими) достаточная, чтобы перевесить дисполезность труда Верхнего (и следовательно, для удовлетворения ограничению участия).
В случае разрешения Нижний определяет оба оптимальных уровня усилий по ловле (e~ и E~ ), а затем дает Верхнему разрешение на ловлю на уровне E~ в ответ на то, что Верхний платит плату за разрешение F. Чтобы учесть ограниче ние участия, запишем предложение Нижнего Верхнему как решение стандарт ной задачи условной максимизации, а именно, изменяя e и E, чтобы максимизи ровать ω = α (1 - βE) e - e2 + F при условии α (1 - βe) E - E2 ≥ F.
Мы знаем, что выполнение ограничения участия Верхнего будет затратным для Нижнего (оба не сыты и не настолько любят свою работу, чтобы бесплатно позволить другому пользоваться ресурсом), таким образом, ограничение выпол няется как равенство. Мы можем использовать это выражение, чтобы исклю чить F из целевой функции. Следовательно, Нижний выберет e и E так, чтобы максимизировать ω = α (1 - βE) e - e2 + α (1 - βe) E - E2.
Заметим, что это как раз и есть общий излишек (общая выгода минус об щая дисполезность труда). Решение задачи (e~ и E~ ) — это план распределения ресурсов Нижнего, реализуемый вместе с планом распределения выгод, требу ющий, чтобы Верхний заплатил сумму F~ = α(1 −βe~ )E~ −E~2 за разрешение рыбачить E~ часов. Поскольку ограничение участия выполнено как равенство, решение становится Паретоэффективным (это одна из точек на кривой эффек тивных контрактов).
Мы можем определить план распределения Нижнего, если установим e и E в соответствии с условиями первого порядка
ωe = α (1 - βE) - 2e - αβE = 0, ωE = α (1 - βe) - 2E - αβe = 0.
Заметим, как эти условия отличаются от ранее определенных условий пер вого порядка для функций индивидуального наилучшего ответа при некоопера тивном взаимодействии: они совпадают, за исключением последнего слагаемого, показывающего влияние ловли Нижнего на благосостояние Верхнего (в первом равенстве) и наоборот (во втором). Решая задачу, получим уровень ловли каж дого
e~ = |
|
|
α |
|
= E~ , |
(4.11) |
|
2 |
+2 |
αβ |
|||||
|
|
|
|||||
который, очевидно, меньше уровня в равновесии по Нэшу (α/(2 + αβ) из равен ства (4.8)) для некооперативного взаимодействия, смоделированного в предыду щем разделе. Заметим, что по мере приближения β к 0 устраняется взаимоза висимость чрезмерного вылова, и равновесие по Нэшу становится решением максимизации совместного излишка, как и следовало ожидать. Распределение, максимизирующее совместный излишек, задано точкой ω на рис. 4.5.
Оптимальное распределение основано на предположении о необходимости ограничения участия. Но почему для Нижнего не будет оптимальным просто вы брать Е = 0 и обладать исключительными правами на озеро? Причина (в данном случае) заключается в том, что предельные издержки компенсирования усилий

Глава 4. Провалы координации и институциональные изменения 137
Верхнего стремятся к 0 по мере того, как Е стремится к 0, поэтому оптимальным становится некоторый положительный уровень Е. (При других разумных спец ификациях модели Нижний исключит Верхнего из ловли — например, если бы Верхний имел выгодную следующую наилучшую альтернативу, тогда Нижнему пришлось бы много платить, чтобы выполнить ограничение участия.)
Вместо того чтобы давать разрешение, Нижний мог бы нанять Верхнего. Эти случаи различаются, поскольку теперь Нижний владеет рыбой, которую Верх ний выловит, но должен отдать часть улова в качестве заработной платы W Вер хнему, достаточной для выполнения его ограничения участия. Знание того, что ограничение участия выполнено как равенство, позволяет нам использовать тот факт, что зарплата должна как раз уравновешивать дисполезность усилий Вер хнего, т. е. W = E2. Нижний теперь должен выбрать e и E таким образом, чтобы максимизировать выражение
α (1 - βE) e - e2 + α (1 - βe) E - W,
которое (при подстановке значения W, заданного из ограничения участия) иден тично задаче, решаемой для случая разрешения. Основные структуры для случа ев выдачи разрешения и найма на работу, следовательно, неразличимы, потому что в обоих случаях Верхний получает только количество, равное дисполезности труда, Нижний выбирает e и E так, чтобы максимизировать совместный изли шек, компенсирует Верхнему дисполезность его труда и оставляет себе остав шуюся прибыль.
Приватизация приводит к Паретоэффективным исходам, потому что агент, принимающий решение, максимизирует при условии связывающего ограниче ния участия другого. Полезность, полученная другим, просто задается его следу ющей наилучшей альтернативой, и таким образом вопрос распределения выгод между ними решается сам собой. В результате владелец — как предъявитель прав на совместный излишек по остаточному принципу — максимизирует свою полезность, выбирая распределение, в котором максимизируется суммарная полезность обоих. Ключ к решению состоит в том, что у владельца достаточно власти, чтобы распределять выгоды независимо от распределения часов ловли; таким образом, у него нет стимулов выбирать распределение, отличное от эф фективного. В гл. 5 я покажу, что так происходит не всегда, и когда независи мость распределения выгод и ресурсов отсутствует, частное распределение ре сурсов становится неэффективным.
Внешнее регулирование. Часто одна сторона не может владеть всеми ре сурсами общего пользования (представьте, как можно установить права на рыбу в открытом океане). И во многих случаях таких ресурсов общего пользования если бы одна сторона всетаки владела всеми ресурсами, то она была бы достаточ но большой, чтобы устранить эффективную конкуренцию на соответствующих рынках. Таким образом, имелись бы знакомые провалы рынков, связанные с ис пользованием рыночной власти. В данном случае правительство или иная внеш няя сторона могла бы улучшить равновесие по Нэшу в некооперативной игре, описанной ранее.
Как и в случае приватизации, возможны две альтернативы. Первая — пла нировщик (правительство) мог бы, зная необходимую информацию, выбрать e

138 Часть I. Координация и конфликт: базовые социальные взаимодействия
и E так, чтобы максимизировать общий излишек. Планировщик мог бы затем реализовать данный исход путем прямого регулирования, просто выдавая раз
решение каждому рыбаку ловить рыбу соответствующее количество времени. Таким образом, точка ω на рис. 4.5 — это оптимальное распределение плани ровщика. Предполагая, что у планировщика нет повода способствовать одному из рыбаков с точки зрения распределения выгод, ω станет точкой распределения как ресурсов, так и выгод. Заметим, что та же точка задает исход распределения ресурсов (но не выгод) в случае приватизации.
Вместо того чтобы применять план распределения с помощью указа, пла нировщик может позволить рыбакам самим выбирать, сколько рыбы ловить, но при этом изменить их стимулы таким образом, чтобы избежать провала ко ординации, имеющего место без государственного регулирования. Это подход к общественному благосостоянию, разработанный экономистами начала XX в. Альфредом Маршаллом и А.С. Пигу (1877—1959) (современная форма подхо да — «теория реализации», упомянутая в гл. 1). В соответствии с данным под ходом планировщик вводит налог на ловлю, вычисленный таким образом, чтобы убрать различие между общественными и частными предельными издержками и выгодами от ловли. Предположим, что сборы отдадут рыбакам обратно в каче стве аккордной суммы, и они не учтут ее в своих подсчетах (как произошло бы в более реалистичном случае, будь рыбаков не двое, а две тысячи). Таким образом, задача планировщика состоит в том, чтобы выбрать налог, при котором бы мак симизировалась суммарная полезность рыбаков, когда рыбаки выбирают, сколь ко рыбы ловить при данном налоге.
Каков размер оптимального налога? Задачу можно поставить таким спосо бом: найти налог, который изменит целевые функции обоих рыбаков так, чтобы их индивидуальные функции наилучшего ответа были бы идентичны получен ным из условия первого порядка в задаче максимизации совместного излишка,
а именно:
e = α(1 −2βE) , 2
E = α(1 −2βe) . 2
Двигаясь в обратном направлении от желаемых условий первого порядка к индивидуальным выигрышам и, следовательно, к налоговой ставке, мы видим, что новая функция полезности uτ должна иметь вид (для Нижнего)
uτ = α (1 - βE) e - e2 - te.
И если условия первого порядка Нижнего должны быть такими же, как при
максимизации совместного излишка, а именно
du τ = α(1 − βE) −2e − αβE = 0, de
то налог на час ловли Нижнего должен составить t = αβE. Проверьте формулу, подставив налоговую ставку в задачу максимизации Нижнего и продифференци ровав по е. В результате должны получиться условия первого порядка такие же,
