Завдання 3

Дослідження фінансових показників діяльності банку (на прикладі Приватбанку)

Визначити залежність кредитування та виплачених відсотків за депозитами від залучених депозитів. Дані наведено нижче.

Обрати специфікацію моделі. Зробити аналіз економетричними методами. Побудувати довірчі зони регресій (обрати рівень значимості самостійно) та пояснити результати.

Зробити висновки

Рік	Відсоткові виплати клієнтам, млн. грн.	Кредити, млн. грн.	Депозити, млн. грн.
	Y	Z	Х
2008	391	23468	9192
2009	802	46621	16939
2010	1129	51867	15007
2011	1232	78290	19962
2012	1090	93683	21084

Завдання 4

Обсяг перевезень товарів за три роки в залежності від кварталу представлено у таблиці:

t	1	2	3	4	5	6	7	8	9	10	11	12
Y	35	62	53	66	74	105	89	95	106	146	114	120

Побудувати модель перевезень за допомогою фіктивних змінних та звичайну парну модель лінійної регресії.

Порівняти результати.

Побудувати графіки для обох моделей.

Знайти оцінки прогнозу (точкову та інтервальну) обсягу перевезень товарів для третього кварталу наступного року.

Рекомендована література

[4, 7, 9, 11]

Тема 2. Моделювання фінансової діяльності із застосуванням виробничих функцій та методів диференційного числення

План вивчення теми

1. Основні поняття, пов’язані з моделюванням за допомогою методів диференціального числення.

2. Еластичність в аналізі фінансової діяльності.

3. Виробничі функції та їх властивості. Еластичність заміщення факторів.

4. Математична теорія фірми. Доход, витрати та прибуток фірми.

5. Аналіз діяльності фірми за допомогою методів диференціального числення. Максимізація прибутку.

6. Бар’єрні показники в фінансовому аналізі.

Навчальні цілі

Ознайомити студентів з особливостями застосування методів та моделей з використанням математичного апарату диференціального числення.

Завдання та методичні рекомендації до вивчення теми

Основні поняття, що пов’язані з моделюванням за допомогою методів диференціального числення: похідна, частинна похідна, граничні (маржинальні) значення функції або показника, еластичність, гранична заміна факторів. Для визначення оптимальних та бар’єрних значень використовуються теореми диференціального числення, що розглядалися в дисципліні «Математика для економістів».

Виробнича функціяпов’язує обсяг випущеної продукції та фактори, що на нього впливають. Використовують різні виробничі функції, виходячи з технології підприємства та його масштабу. Виробничі функції описують процеси і на окремих підприємствах, і в окремих галузях, і в економіці всієї країни.

З видами і застосуванням виробничих функцій можна ознайомитися у літературі , список якої наведено в кінці методичних рекомендацій до даної теми.

Однією з найпоширеніших є виробнича функція Кобба-Дугласа та мультиплікативна функція типа Кобба-Дугласа. Розглянемо більш докладно останню.

Мультиплікативна функція має вигляд:

,,, (21)

де обсяг випущеної продукції;

основні засоби підприємства;

працезатрати;

–параметри моделі.

Мультиплікативна функція застосовується для моделювання на макро- та мікрорівнях.

Для визначення параметрів моделі можна застосувати метод найменших квадратів. Для цього нелінійну модель треба звести до лінійної форми. Після логарифмування

(22)

і заміни змінних ,,, отримаємо приведену лінійну регресію:

, (23)

де .

Далі обчислюємо параметри регресії, визначаємо якість та адекватність моделі, визначаємо границі надійних інтервалів для параметрів і прогнозу показника, як для множинної лінійної моделі. Для параметра та границь надійного інтервалу прогнозу показника треба зробити зворотні перетворення: знайти за допомогою потенціювання.

Приклад розрахунку параметрів виробничої функції докладно наведено у навчально-методичному посібнику «Економіко-математичні методи та моделі. Частина 2» [4].

Зупинимося на питаннях, що раніше не розглядалися.

Частковим випадком неокласичної мультиплікативної виробничої функції є функція Кобба-Дугласа:

,,. (24)

Зі зростанням витрат ресурсів випуск також зростає, про що свідчать частинні похідні випуску:

, оскільки; (25), оскільки. (26)

Здійснимо економічну інтерпретацію параметрів мультиплікативної виробничої функції [1].

Параметр А інтерпретують як параметр нейтрального технічного прогресу: за тих самих значеньтавипуск буде тим більшим, чим більшеА.

Параметри та- коефіцієнти еластичності випуску за основними фондами та працею відповідно. Якщо>, то має місце працеощадне (інтенсивне) виробництво; якщо<, виробництво є екстенсивним.

Граничною нормою заміни праці фондами називають відношення:

, (27)

і, відповідно, гранична норма заміни фондів працею:

. (28)

Для наочного уявлення взаємозамінюваності факторів можна побудувати ізокванту – геометричне місце точок факторів, для яких показник обсягу виробництва продукціїзалишається сталим. Щоб побудувати ізокванту, виразимо один із факторів виробничої регресії через інший фактор і стале значення показника регресії Y₀:

. (29)

Якщо сталу позначити через b, то отримаємо таку залежність: .

Частинні похідні випуску за чинниками називають граничними продуктами або граничними (маржинальними) ефективностями чинників.

Легко помітити, що .

Для мультиплікативної виробничої функції норма заміщення праці фондами пропорційна фондоозброєності:

,, (30)

що є логічним, адже брак обсягів праці можна компенсувати кращою фондоозброєністю.

За допомогою ВФ можна описати ефективність та масштаб виробництва.

Перейдемо до відносних (безрозмірних) показників у ВФ:

, деX₀ ,K₀, L₀ –значення обсягів випуску і витрат фондів та праці в базовому році.

Приведемо безрозмірну форму до початкового вигляду виробничої функції:

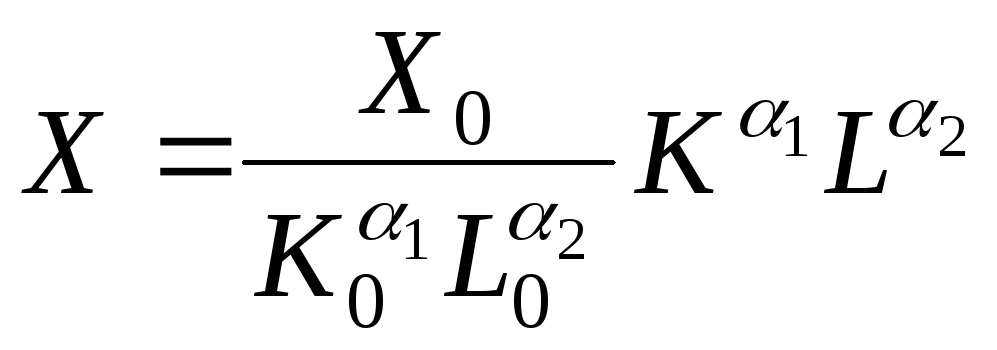. (31)

Отже, коефіцієнт Азіставляє ресурси з випуском.

У відносних (безрозмірних) одиницях ВФ можна записати таким , (32)

де ,,. (33)

Ефективність – це відношення результату до витрат. У нашому випадку є два часткових показника ефективності: - фондовіддача;- продуктивність праці. Коефіцієнт ефективності можна записати у такій формі:

, (34)

роль вагових коефіцієнтів тут відіграють відносні еластичності за фондами і працею:

,, (35)

тобто часткові ефективності входять до загальної ефективності з такими самими пріоритетами, з якими входять у ВФ відповідні ресурси.

За допомогою коефіцієнта економічної ефективності ВФ можна подати у формі, яка зовнішньо збігається з функцією Кобба-Дугласа:

. (36)

Масштаб виробництва визначається як середнє геометричне темпів зростання використаних ресурсів:

. (37)

Отже, випуск є добутком економічної ефективності та масштабу виробництва:

. (38)

Математична теорія фірми, зокрема, оптимізаційні задачі в різних сферах людської діяльності пов’язані із поняттям похідної. Розв’язування таких задач засновано на дослідженні функцій методами диференціального числення.

Розглянемо задачу максимізації прибутку фірми, яка випускає продукцію одного виду. Розрізняють випадки досконалої ринкової конкуренції і монополії щодо ціни на продукцію. Докладно – в рекомендованій літературі [2].

Розглянемо випадок сталої ціни. Якщо підприємство виробило продукції одиниць (кг, тон і т.ін.), то при її реалізації за ціноюдохід складе:

. (39)

Функція витрат визначається розподілом вихідних даних. Якщо розподіл витрат, наприклад, можна описати квадратичною функцією, то відповідна регресія має вигляд:

. (40)

Це рівняння треба звести до лінійного заміною змінних і визначити параметри економетричними методами, використовуючи вихідні дані. (див. навчально-методичний посібник «Економіко-математичні методи та моделі. Частина 2», тема 3 [4]).

Прибуток визначиться таким чином:

. (41)

Для визначення максимуму прибутку треба задовольнити необхідну умову екстремуму функції однієї змінної:

. (42)

З цього рівняння отримаємо значення , за якого функція прибутку має екстремум:

. (43)

З огляду на те, що функція прибутку квадратична, опукла вгору, то маємо максимум. У цьому можна переконатися, якщо знайти другу похідну функції прибутку, і, таким чином, задовольнити достатню умову існування екстремуму.

Щоб знайти максимальний прибуток, треба визначене значення у підставити у функцію прибутку.

В оптимальному розв’язку маржинальний дохід та маржинальні витрати мають однакові значення.