Дополнительные темы
Представленное выше описание абстрактных типов данных вполне достаточно для использования АТД в рамках данной книги. (Чтобы дополнить его, выполните упражнения, которые помогут уточнить ваше понимание этого понятия).
Если же, как я надеюсь, АТД уже завоевали вас своей элегантностью, простотой и мощью, то не исключено, что вам захочется узнать побольше об их свойствах, даже о таких, которые не будут использоваться в обсуждении ОО-методов. Далее на нескольких страницах рассмотрены следующие дополнительные темы, которые можно опустить при первом чтении:
*неявность и ее связь с процессом конструирования ПО;
*различие между спецификацией и проектированием;
*различие между классами и записями;
*возможные альтернативы использованию частичных функций;
*решение о полноте или неполноте спецификации.
Библиографические ссылки к этой лекции указывают на более специальную литературу по АТД.
Еще раз о неявности
Неявная природа абстрактных типов данных и классов, рассмотренная выше, отражает одну из важных проблем конструирования программ.
Вполне законен вопрос о различии между упрощенной спецификацией АТД, использующей объявление функций
x:POINT -> REAL
y:POINT -> REAL
и объявлением типа в таком традиционном языке программирования, как Pascal:
type POINT = record
x, y: real end
На первый взгляд эти два объявления представляются эквивалентными: оба утверждают, что с типом POINT связаны два значения x и y т и п а REAL. Но между ними имеется существенная, хотя и тонкая разница:
*Запись в языке Pascal является законченной и явной: она показывает, что объект POINT включает два данных поля и ничего кроме них.
*Объявление функций АТД не несут такого смысла. Они показывают, что объект типа POINT можно запрашивать о значениях его x и y, но не исключают других запросов, например, о массе и скорости точки в кинематическом приложении.
С упрощенной математической точки зрения можно считать, что приведенное выше объявление в Паскале является определением математического множества POINT как декартова произведения:
где знак 
означает "определяется как" ("равно по определению"), и оно полностью задает POINT. В отличие от этого спецификация АТД не определяет явно POINT посредством такой математической модели как декартово произведение, она просто неявно характеризует POINT, перечисляя два запроса, применимых к объектам этого типа.
Если имеются спецификации некоторого понятия, то может появиться желание переместить ее из неявного мира в явный, идентифицируя понятие с декартовым произведением применимых к нему простых запросов, например захочется идентифицировать точки с парами <x, y>. Такой процесс идентификации можно рассматривать как определение перехода от анализа и спецификации к проектированию и реализации.
Соотношение спецификации и проектирования
Предыдущее наблюдение помогает уточнить один из центральных вопросов, возникающих при изучении ПО: различие между начальным этапом разработки ПО - его спецификацией, называемым также анализом, - и более поздними стадиями такими, как проектирование и реализация.
В литературе по разработке программ обычно объясняется, что это различие между "определением задачи" и "построением ее решения". Будучи в принципе правильным, такое объяснение не всегда применимо на практике и иногда бывает трудно понять, где заканчивается спецификация и начинается проектирование. Даже в среде исследователей люди запросто критикуют друг друга в связи с этой темой: "вы рекламируете язык x как язык спецификаций, но на самом деле он предназначен для проектирования". Наивысшим оскорблением считается обвинение некоторой системы обозначений в обслуживании реализации (подробнее об этом в одной из следующих лекций).
Приведенное выше определение дает более точный критерий: пересечь Рубикон между спецификацией и проектированием - это перейти от неявного к явному, другими словами:
Определение: переход от анализа (спецификации) к проектированию Перейти от спецификации к проектированию - это идентифицировать каждую
абстракцию с декартовым произведением ее простых запросов.
Последующий переход - от проектирования к реализации - это просто движение от одного явного вида к другому: форма при проектировании более абстрактна и ближе к математическим понятиям, а при реализации более конкретна и ближе к компьютеру, но обе они являются явными. Этот переход менее драматичен, чем предыдущий - действительно, при дальнейшем чтении станет понятно, что объектная технология почти стирает различие между проектированием и реализацией. При хорошей системе ОО-нотации нашими компьютерами непосредственно выполняется (с помощью компиляторов) то, что в не ОО-мире часто рассматривалось бы как проекты.
Соотношение классов и записей
Другим замечательным свойством объектной технологии является то, что при ней можно сохранять неявные описания гораздо дольше, чем при других подходах. В последующих лекциях будет введена система обозначений, позволяющая определять класс в виде:
class POINT feature x, y: REAL
end
Это выглядит подозрительно похожим на приведенное выше определение записи в Паскале. Но, несмотря на внешнее сходство, определение класса другое - оно неявное! Эта неявность проявляется при наследовании: автор класса или (что еще более интересно) кто-либо другой может в любой момент определить новый класс, например:
class MOVING_POINT inherit POINT
feature mass: REAL
velocity: VECTOR [REAL] end
который расширяет исходный класс совершенно незапланированным способом. Тогда переменная (или сущность, если использовать вводимую далее терминологию) типа POINT, объявленная как
p1: POINT
может быть связана с объектом не только типа POINT, но и с каждым потомком этого типа, например с объектом типа MOVING_POINT. Это может получиться, в частности, с помощью "полиморфных присваиваний" вида:
p1 := mp1
где mp1 имеет тип MOVING_POINT.
Эти возможности иллюстрируют неявность и открытость определения класса: соответствующие экземпляры представляют не только точки в узком смысле, т. е. непосредственно экземпляры класса POINT, но и экземпляры всякого класса, описывающего понятия, выводимые из исходного класса.
Способность определять элементы программ (классы), которые немедленно используются (посредством наследования), оставаясь неявными, является одним из главных нововведений объектной технологии, непосредственно отвечающему принципу Открыт-Закрыт. В последующих лекциях будут раскрыты все вытекающие из нее следствия.
Альтернативы частичным функциям
Один из технических приемов, используемый в этой лекции, мог вызвать удивление, - применение частичных функций. Он связан с неустранимой проблемой применения в некоторой спецификации не всюду определенных операций. Но являются ли частичные функции лучшим решением этой проблемы?
Конечно, это не единственно возможное решение. Другим способом, который приходит на ум и действительно используется в некоторых работах по АТД, является превращение частичной функции во всюду определенную за счет введения специального значения "ошибка" для случаев применения функции к неподходящим аргументам.
Каждый тип T дополняется значением "ошибка". Обозначим его через wT. Тогда для всякой
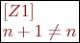
функции f сигнатура
f: ... Типы входов ... -> T
определяет, что всякое применение f к объекту, для которого соответствующее вычисление не может быть выполнено, выдаст значение wT.
Хотя этот метод и используется, он приводит к математическим и практическим неудобствам. Проблема в том, что такие специальные значения являются весьма эксцентричными существами, которые могут чрезвычайно осложнить жизнь невинных математических существ.
Предположим, например, что рассматриваются стеки целых чисел - экземпляры типа STACK [INTEGER], где INTEGER - это АТД, экземпляры которого - целые числа. Хотя для нашего примера не требуется полностью выписывать спецификацию INTEGER, этот АТД должен моделировать основные операции (сложение, вычитание, "меньше чем" и т. п.), определенные на математическом множестве целых чисел. Аксиомы этого АТД должны выражать обычные свойства целых чисел. Вот одно из таких типичных свойств: для всякого целого n:
Пусть теперь n будет результатом запроса верхнего элемента пустого стека, т. е. значением выражения item (new), где new - это пустой стек целых чисел. При этом запросе n должно получить специальное значение wINTEGER. Что же тогда должно быть значением выражения n+1? Если у нас в распоряжении имеются в качестве значений только обычные целые числа и wINTEGER, то в качестве ответа мы вынуждены выбрать wINTEGER:
wINTEGER + 1 = wINTEGER.
Это единственный допустимый выбор. Если присвоить wINTEGER+1 любое другое значение, "нормальное" число q, то это означает, что после попытки доступа к вершине пустого стека и получения в качестве результата ошибочного значения мы можем волшебным образом устранить всякую память об этой ошибке, просто прибавив к результату единицу!
Но, при выборе wINTEGER в качестве значения n + 1 при n равном wINTEGER, нарушается указанное выше свойство Z1. В общем случае, выражение wINTEGER+p будет равно wINTEGER для любого p. Это означает, что для измененного типа данных ( INTEGER, дополненные ошибочным элементом) требуется новая система аксиом, объясняющая, что всякая операция над целыми числами возвращает значение wINTEGER, если хоть один из ее аргументов равен wINTEGER. Аналогичные изменения потребуются для каждого типа.
Получившееся усложнение не кажется обоснованным. Мы не можем изменять спецификацию целых чисел только для того, чтобы промоделировать каждую отдельную структуру данных (в нашем случае - стеки). При использовании частичных функций ситуация более простая. Конечно, для всякого выражения, содержащего частичные функции, приходится проверять, что их аргументы удовлетворяют соответствующим предусловиям. После завершения такой проверки, можно беспрепятственно применять аксиомы. При этом не требуется изменять существующие системы аксиом.