Задача 2. Оцінка «тісноти» зв'язку між змінними.

«Тіснота» зв'язку може бути оцінена графічно по розташуванню експериментальних крапок щодо теоретичної лінії регресії.

Для кількісної оцінки «тісноти» і напряму лінійного зв'язку між змінними використовується коефіцієнт кореляції:

;

.

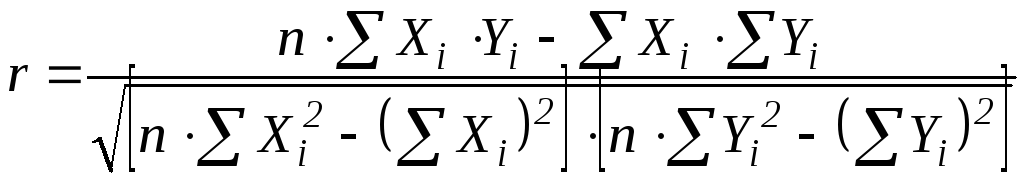Діапазон зміни коефіцієнта кореляції: .

Характерні значення коефіцієнта кореляції представлені на рис.2.10.

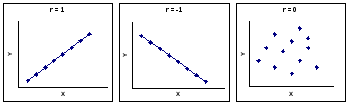
Рис.2.10. Граничні значення коефіцієнта кореляції

Вважають:

- зв'язок дуже слабкий;

- зв'язок сильний;

- зв'язок є.

Для оцінки «тісноти» зв'язку при будь-якій формі зв'язку використовується кореляційне відношення:

,

Де R² - коефіцієнт детерміації.

Діапазон зміни: .

Коефіцієнт детерміації показує частку загального коливання (варіації, зміни, розкиду) результату У, з'ясовного коливанням чинників, що враховуються (X):

,

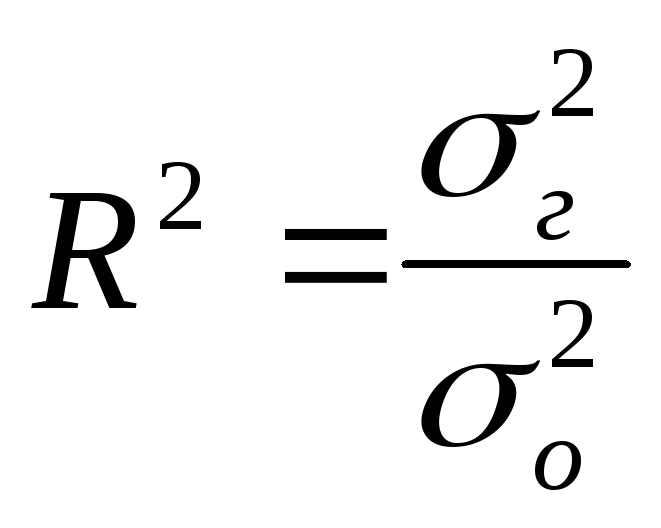де

- міжгрупова дисперсія (дисперсія чинника, що відображає вплив тільки врахованих чинників (Х) на той, що коливається, результат (Y);

- загальна дисперсія, що відображає вплив всіх чинників (як врахованих, так і не врахованих) на той, що коливається, результат (Y).

При виконанні певних умов загальна дисперсія може бути представлена сумою міжгрупової і залишкової дисперсії:

,

де - залишкова дисперсія, що оцінює той, що коливається результату У під впливом всіх неврахованих чинників.

Через визначення R² приймає значення між 0 і 1 .

Якщо R² = 0, то це означає, що регресія нічого не дає.

Інший крайній випадок R² = 1 означає точну підгонку: всі експериментально одержані крапки лежать на регресійній прямій.

Чим ближче до 1 значення R², тим краще якість підгонки, точніше апроксимує У.

Наприклад, якщо R² = 0,80, то коливається У на 80% пояснюється X.

Недолік коефіцієнта детермінації – його значення не відображає напрям зв'язку між досліджуваними змінними.

Дисперсія характеризує розсіювання (ступінь «розкиду») випадкової величини навколо її математичного очікування (середнього значення).

Якщо використовувати позначення:

- фактично набуті в експерименті значення У при спостережуваних значеннях ;

- розрахункові (по оціненому аналітичному рівнянню регресії) значення У при спостережуваних значеннях ;

- середнє значення У для даного масиву експериментально одержаних даних,

то дисперсії можуть бути обчислені по наступних виразах.

Загальнадисперсія

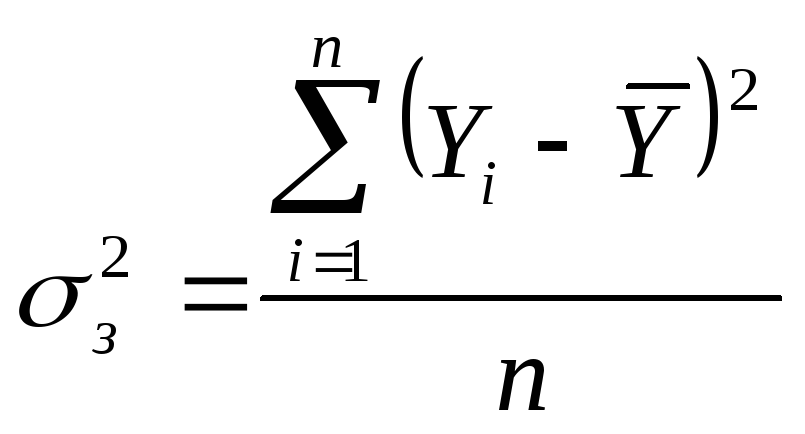. (2.1)

Міжгрупова дисперсія

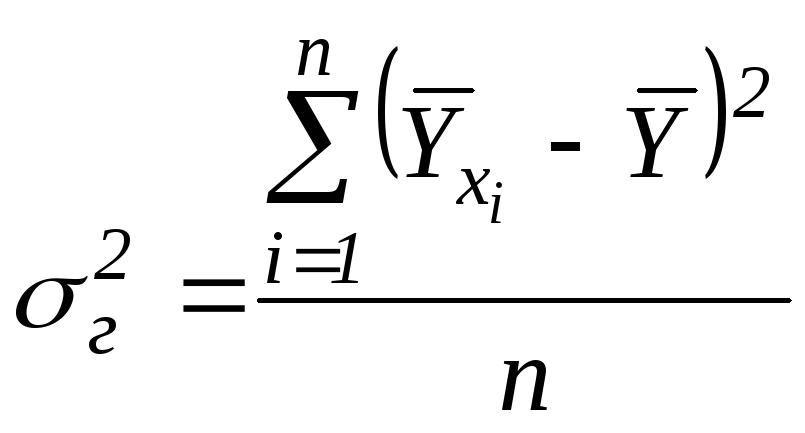. (2.2)

Залишкова дисперсія

. (2.3)

Увага! "n" у формулах (2.1) – (2.3) повинне бути обов'язково однаковим. Тому якщо при одному і тому ж в серії експериментів набуто декілька значень У, розрахункові значення У необхідно обчислити при тих же, що і в експерименті, тобто узяти стільки крапок, скільки в експерименті.

Відобразимографічно (рис.2.11).

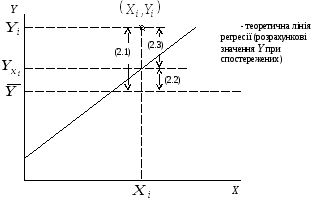
Рис.2.11. До питання визначення загальної, міжгрупової і залишкової дисперсії

Дані для розрахунку загальної, міжгрупової і залишкової дисперсії для даного прикладу представлені в табл.2.3.

Таблиця 2.3 – Дані для розрахунку дисперсії

i
1	0,1444	0,16322	0,00058
2	0,0529	0,09181	0,00533
3	0,0169	0,00000	0,01690
4	0,0144	0,09181	0,03349
5	0,3844	0,16321	0,04665
Σ	0,6130	0,51005	0,10295

Тоді для даного прикладу коливається У пояснюється тим, що коливається X на 83,2%, оскільки

.