УстрАСУ / Конспект УАСУ

301 moteur asynchrone a cage commande par contacteur statique,—С. г. Acad. sci., 1979, AB 288, N 17, p. 274-280.

59. Variable Speed a. c. drives.— Power and Works bng, 1978, N 18, p. 23.

60.Wechselstromsielles гиг Drehzahlregulung von Asynchron-motoren.— Ind— Anz., 1979, N 13, s. 17.

61.Wehrmann С Reguiung von Drehstrommotoren nach dern Spannungssteller—und Umrichterverfahren.— Ind. und Masch. Rept. Int, 1979, N 2 s. 38—42.

301

ЛЕКЦИЯ 30. СИНХРОННЫЕ МАШИНЫ (СМ)

7.1.ЭЛЕМЕНТЫ ТЕОРИИ РАБОЧЕГОПРОЦЕССА СМ

Всистемах генерирования переменного тока стабильной и переменной частоты на самолетах в качестве главных генераторов переменного тока используются синхронные генераторы (СГ). В приводах механизмов и приборов с постоянной частотой вращения используются синхронные двигатели (СД). Для синхронной передачи вращения с одного вала на другой без механической связи (например, внутрь тонкостенного трубопровода с топливом или агрессивной средой) используются синхронные муфты.

Для СМ, включая специальные электродвигатели, характерная для них жесткая связь

между частотой вращения ротора п и синхронной частотой вращения поля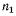может быть

Теория СМ разработана достаточно детально. Наиболее общим подходом исследования является метод, основанный на общих уравнениях динамики СМ, которые следуют из уравнений обобщенного ЭМП.

302

303

Вначале упрощенно, не используя общие уравнения динамики ЭМП, рассмотрим некоторые особенности установившегося режима СМ.

Основной магнитный поток возбуждения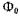 в классических СМ имеет радиальное направление, жестко связан с индуктором и при вращении создает вращающееся относительно якоря магнитное поле с частотой вращения ротора.

При вращении индуктора относительно якоря в каждой фазе обмотки СГ при разомкнутых якорных выводах (XX генератора) согласно закону электромагнитной индукции наводится ЭДС XX, мгновенное значение которой определяется соотношением

Таким образом, в синхронных генераторах основная ЭДС взаимоиндукции обмотки якоря возникает в результате периодического изменения взаимной индуктивности между обмотками возбуждения и якоря при их относительном перемещении. Из этого положения вытекает принципиальная возможность создания синхронных машин с электромагнитным возбуждением, не имеющих скользящих щеточных контактов. Это так называемые бесконтактные, или бесщеточные машины. Действительно, в традиционных синхронных машинах (рис. 7.1) взаимная индуктивность MkB изменяется по периодическому закону в силу периодического изменения положения магнитных осей обмоток при вращении

ротора. Такого же эффекта и изменения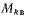в соответствии с (7.2) можно добиться при неподвижном положении обмоток относительно друг друга, но при периодическом изменении магнитной проводимости на пути магнитного потока возбуждения, сцепляющегося с фазами обмотки якоря.

Основные электромагнитные процессы в классических и бесконтактных СМ аналогичны, а особенности бесконтактных СМ будут рассмотрены отдельно.

7.1.1. РЕАКЦИЯ ЯКОРЯ В СМ

Прежде чем перейти к уравнениям СМ рассмотрим кратко фундаментальное в теории СМ (как и других типов ЭМ) понятие реакции якоря. Под реакцией якоря понимают воздействие, или влияние МДС обмотки якоря на результирующий магнитный поток рабочего зазора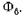Реакция якоря проявляется в том, что при нагрузке СМ результирующий магнитный поток в воздушном зазоре и форма кривой распределения индукции отличаются от потока и распределения магнитной индукции в режиме XX при

303

304

неизменной МДС возбуждения. В синхронных генераторах реакция якоря является основной причиной того, что напряжение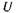в режиме нагрузки значительно отличается от напряжения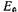в режиме XX при неизменной МДС возбуждения и постоянной частоте вращения.

В синхронных двигателях реакция якоря проявляется в том, что магнитный поток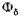и форма кривой распределения индукции при неизменной МДС возбуждения зависят от внешнего момента на валу (нагрузки) и связанного с ним тока якоря.

Рассмотрим это явление на примере СГ, а в дальнейшем покажем, что ряд характерных параметров, связанных с явлением реакции якоря, в равной мере играет существенную роль в электромагнитных процессах как в СГ, так и в СД. Именно общность ряда параметров СМ независимо от режима работы (генератор, двигатель) обусловливает распространение понятия реакции якоря и на СД с возбужденным и невозбужденным ротором. Явление реакции якоря в СГ рассмотрим на примере явнополюсной СМ с вращающимся индуктором и неподвижным якорем-статором, так как и в других типах СГ

где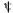— угол сдвига фаз между ЭДС XX и током, определяется известным из теории МДС обмоток переменного тока соотношением

фазе (эффективное); р — число пар полюсов; х — текущая линейная координата перемещения МДС по развертке длины окружности якоря;— полюсное деление. Из уравнения

положение в пространстве максимума МДС обмотки якоря, которое зависит от времени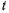 и угла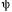между ЭДС XX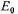и током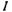(в зависимости от характера нагрузки), определяется как

возбуждения 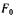При этом пространственный угол между пространственными векторам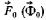ии

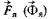, неподвижными относительно друг друга, при синхронном вращении (рис. 7.2) изменяется в зависимости от характера нагрузки в пределах 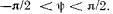При 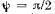(чисто

индуктивная нагрузка, ток отстает от ЭДС напротивонаправлена по отношению к

304

реакция якоря проявляется в виде искажения картины магнитного поля, не оказывая непосредственно подмагничивающего и размагничивающего воздействия, если магнитная цепь не насыщена. Очевидно, что в явнополюсной машине с изменением угла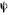будет

случае при количественном анализе необходимо вводить переменное магнитное сопро-

встречно по отношению к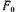и размагничивает магнитную систему, а при опережающем токе (при активно-емкостном характере нагрузки) 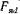совпадает по направлению с 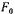и подмагничивает магнитную систему генератора. В методе двух реакций магнитные

достаточно просто производить количественный учет для компенсации реакции якоря, если МДС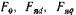привести к единому масштабу. Для количественного учета реакции якоря с целью компенсации размагничивающего или подмагничивающего действия реакции якоря соответствующим изменением МДС возбуждения (тока возбуждения) необходимо знать, какая МДС якоря эквивалентна некоторому значению МДС возбуждения. Другими словами, необходимо составляющие МДС якоря привести к масштабу МДС возбуждения, что осуществляется посредством коэффициентов приведения

305

306

поперечной и продольной реакции якоря 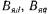и поля возбуждения 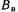В явнополюсных СМ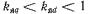. В неявнополюсных СМ 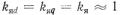в силу равенства магнитных сопротивлений 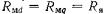для потока якоря при любом 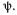Чтобы скомпенсировать действие реакции якоря, необходимо при нагрузке генератора током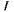так изменить МДС обмотки возбуждения, чтобы магнитный поток воздушного зазора при холостом ходе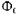был равен магнитному потоку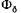при нагрузке. МДС возбуждения нагруженного генератора для 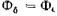при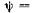 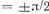соответственно неявнополюсной и явнополюсной СМ определяется как

Поперечная реакция якоря может оказывать размагничивающее действие лишь при насыщенной магнитной системе, когда при поперечном направлении МДС якоря подмагничивание одного края полюса в соответствии с нелинейной кривой намагничивания стали происходит в меньшей степени, чем размагничивание другого края полюса. На рис. 7.4 представлена картина распределения токов якоря, потоков и взаимное расположение первых гармоник поля возбуждения и поля якоря. Если при синхронном вращении рассматривать момент времени, когда ток в одной из фаз достигает максимума, то ось результирующей МДС якоря от всех фаз совпадает с осью этой фазы. Это положение и позволяет заменить фаз одной эквивалентной фазой, представленной на рис. 7.4, в которой ток достигает максимума. При этом весьма наглядно можно проследить действие реакции якоря при различном характере нагрузки.

Реакция якоря определяет так называемые синхронные параметры синхронных машин.

Применяя принцип наложения, можно считать, что потоки 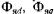неявнополюсной и явнополюсной СМ наводят в обмотке якоря ЭДС,

действующее значение первых гармоник которых определяются соотношениями:

Рис. 7.4. Картина распределения токов якоря и магнитных потоков при активной (а), индуктивной (б) и емкостной (в) нагрузках.

/ — первая гармоника поля якоря; 2 — первая гармоника поля возбуждения; 3 — результирующее поле.

рассеяния обмотки якоря, называют синхронными индуктивными сопротивлениями

306

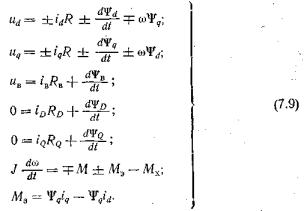
307

неявнополюсной и явнополюсной СМ по продольной и поперечной осям (продольное и поперечное синхронные индуктивные сопротивления). Физический смысл синхронных индуктивных сопротивлений можно объяснить, исходя из следующего воображаемого опыта. Обмотку якоря СМ подключают к трехфазной сети переменного тока, в результате чего создается вращающееся с угловой скоростью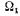магнитное поле якоря 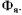Невозбужденный индуктор вращают синхронно с полем. Если магнитный поток якоря замыкается по продольной оси машины 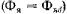, то СМ при пренебрежении активным сопротивлением обмотки якоря 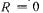для сети будет представлять собой индуктивное сопротивление а ток, потребляемый из сети, будет продольным током Если поток якоря замыкается по поперечной оси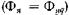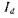, то СМ для сети будет являться индуктивным сопротивлением, а ток, потребляемый из сети, — поперечным током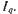 Поскольку индуктивные сопротивления пропорциональны магнитным проводимостям, а в явнополюсной машине магнитная проводимость по продольной оси больше, чем по поперечной то 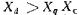, Очевидно, что в неявнополюсных СМ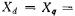

Выяснив физический смысл синхронных индуктивных сопротивлений, связанных с явлением реакции якоря, нетрудно видеть, что эти параметры присущи любой СМ, независимо от режима ее работы: генератор, двигатель с возбужденным или невозбужденным ротором. В этом заключается общность в проявлении реакции якоря всех типов СМ, хотя количественное выражение этих параметров и их соотношение существенно зависят от конкретного типа СМ.

7.1.2. УРАВНЕНИЯ ДИНАМИКИ СМ

Уравнения динамики описывают переходные процессы, частным случаем которых является установившийся режим. Для СМ эти уравнения получаются как частный случай общих уравнений, описывающих процессы ЭМП.

Для того чтобы избавиться от периодических коэффициентов и тем самым упростить систему дифференциальных уравнений ЭМП, как показано в гл. 3, их записывают в системе ортогональных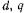— координат, или, как говорят, преобразуют к осям 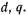Для синхронных машин это преобразование впервые было выполнено Парком и Горевым. Система преобразованных уравнений СМ, не содержащих периодических коэффициентов (уравнения с постоянными коэффициентами),получила название уравнений Парка—Горева. В СМ ортогональные оси 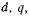к которым преобразуются исходные уравнения, совпадают с продольной и поперечной осями, используемыми в изложенном выше методе двух реакций.

Уравнения синхронной машины в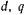координатах, описывающие переходные электромагнитные и электромеханические процессы (уравнения Парка—Горева), имеют вид:

307

308

Верхние знаки в (7.9) относятся к двигательному, а нижние — к генераторному режимам работы. Индексыотносятся к якорной цепи по 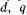-осям, а «в», 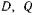— к обмотке возбуждения и демпферной обмотке по осям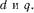

Обычно параметры обмотки возбуждения и демпферной обмотки приводят к числу витков обмотки якоря подобно тому, как это делается для трансформаторов. Кроме того, уравнения представляют в относительной безразмерной форме, выбирая соответствующим образом базисные напряжение, ток, потокосцепление и сопротивление, а дифференцирование производят по так называемому синхронному времени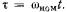При этом потокосцеп-ления в уравнениях (7.9), которые в относительной форме сохраняют тот же вид, выражаются как

Уравнения (7.9) и (7.10) представляют собой полную систему нелинейных дифференциальных уравнений с постоянными ■ коэффициентами, которые описывают динамику СМ. Эти уравнения содержат нелинейности типа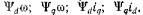

При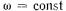они становятся линейными, а уравнение движения ротора выпадает из рассмотрения в динамике, так как в этом случае не является дифференциальным.

На основе (7.9), (7.10) строятся математические модели СМ для исследования

Характер переходных процессов в СМ определяется так называемыми переходными и

Лапласу с нулевыми начальными условиями (токи, напряжения, потокосцепления представляются в отклонениях от их значений в исходном установившемся режиме: 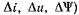, то из (7.9) и (7.10) в области изображений по Лапласу можно получить:

демпферная обмотка отсутствует, то

308

309

В переходных процессах (внезапное КЗ генератора, наброс нагрузки и т. п.) оригиналы операторных коэффициентов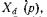 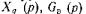мотонно возрастают во времени 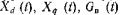в пределах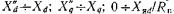, При наличии демпферной обмотки в некоторый момент времени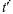(несколько периодов переменного тока)

свободная составляющая тока в демпферной обмотке затухает до нуля вследствие рассеяния энергии в 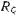. При этом . 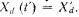Оригиналы можно представить в виде:

Параметры определяют всплески токов и электромагнитного момента при внезапном КЗ генератора, которые многократно превышают номинальные значения. Эти же параметры определяют начальный нерегулируемый спад напряжения при набросе нагрузки на генератор. Начальная стадия этого процесса является нерегулируемой по той

причине, что Это означает, что на начальной стадии (интервал времени в несколько периодов переменного тока) реакция цепи якоря на изменение напряжения возбуждения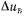равна нулю: скачкообразное изменениене приводит к мгновенному изменению потокосцепления и, следовательно, не может изменить ЭДС и напряжение.

электромагнитных связей между обмотками и постоянство частоты вращения. При этом уравнения электрического равновесия принимают вид:

где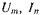— амплитудные значения фазных напряжений и тока.

Уравнение цепи возбуждения не представляет интереса, а напряжения псевдонеподвижных обмоток с учетом выражений потокосцеплений (7.10)

при 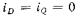принимают вид:

309

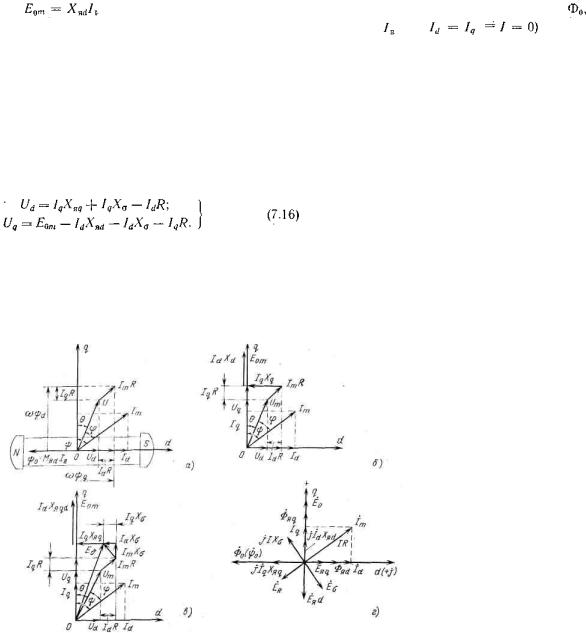
каждую из составляющих (7.15) в масштабе напряжения представить вектором в осях 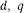, то мы получим диаграмму напряжений в пространственных осях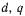. Для генераторного режима при активно-индуктивном характере нагрузки в соответствии с (7.14) и (7.15) она представлена на рис. 7.5, а, б. Здесь же показано принятое положительное направление осей 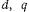и токов. Из рис. 7.5, б следует, что при активноиндуктивном характере нагрузки напряжение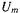меньше ЭДС холостого хода .за счет падения напряжения в. Непосредственно на диаграмме напряжений действие реакции якоря можно выяснить, если (7.15) для генераторного режима представить в виде

Уравнениям (7.15) при активно-индуктивном характере нагрузки соответствует диаграмма напряжений, приведенная на рис. 7.5, в. Падения напряжений в правых частях (7.16) по модулюравны соответствующим ЭДС: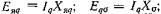

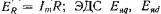и наводятся соответственно потоками якоря 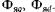а ЭДС рассеяния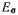— потоком рассеяния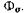

Рис. 7.5. Диаграммы напряжений синхронного генератора при активно-индуктивном характере нагрузки. а, бв в — в пространственных осях г — в комплексной плоскости.

Как известно, уравнения электрического равновесия цепей переменного тока представляют в комплексных величинах, а соответствующие им векторные диаграммы — на комплексной плоскости. Диаграммы напряжений СМ также можно представить на комплексной плоскости, которые называют векторными диаграммами СМ. Теоретически связь между токами и напряжениями в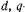-координатах и комплексными векторами токов и напряжений показана в гл. 3. Комплексные оси можно совместить на. плоскости с осямиЭто сделано на рис. 7.5, г, где представлены векторы комплексных величин (7.16), причем с осью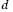совмещена положительная мнимая ось, а с

осью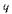— положительная действительная. Диаграмма рис. 7.5, г объясняет то обстоятельство, что на рис. 7.4,б и в векторы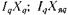направлены по продольной оси, а векторы

310