
МУ 15-42 ФИЗИКА Алмаз
.pdf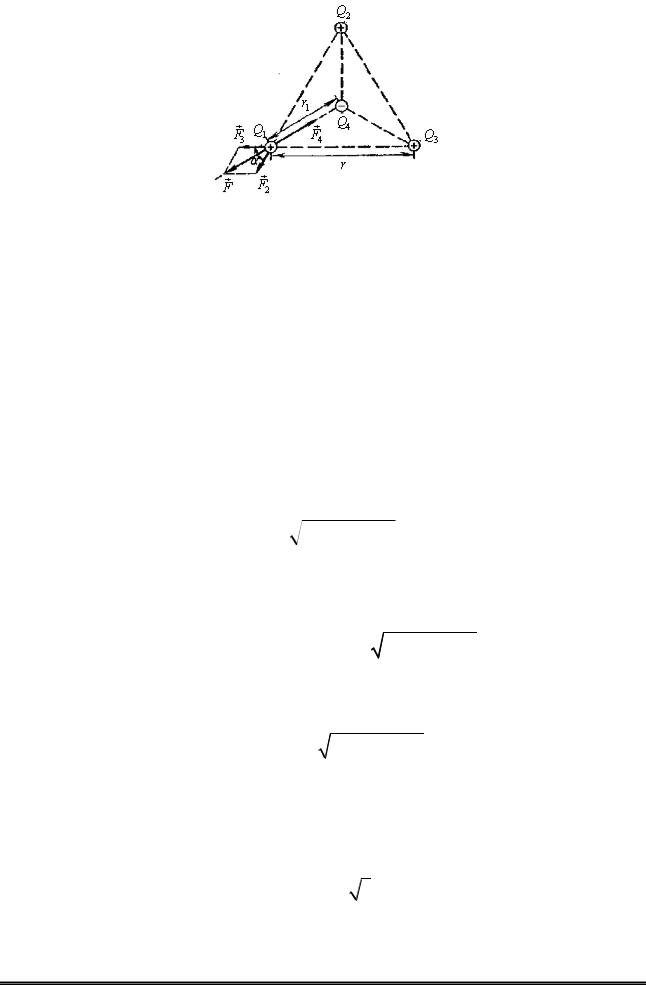
81
Рисунок 7 – Рівновага системи чотирьох зарядів
F2 F3 F4 F F4 0, |
(1) |
де F2, F3, F4 – сили, з якими відповідно діють на заряд Q1 заряди
Q2 , Q3, Q4 ;
F – рівнодіюча сил F2 та F3.
Оскільки сили F і F4 направлені по одній прямій в протилежні сторони, то векторну рівність (1) можна замінити скалярною: F F4 0, звідки F4 F. Визначив в останньої рівності F через F2 і F3 та враховуючи, що F3 F2, отримаємо:
F4 F2 
 2(1 cos α).
2(1 cos α).
Застосувавши закон Кулона й маючи на увазі, що Q2 Q3 Q1, знай-
демо:
|
|
|
|
|
Q2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 4 |
|
|
|
1 |
|
|
2(1 cos α), |
|
|||||||
|
|
|
|
2 |
|
|
|
|
r2 |
|
|||||||
|
4 |
r |
|
|
4 |
0 |
|
|
|
|
|
||||||
звідки |
|
0 1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Q2r |
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Q |
|
|
1 1 |
|
|
2(1 cos α). |
(2) |
||||||||||
|
|
|
|||||||||||||||
4 |
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
||
З геометричних побудов у рівносторонньому трикутнику випливає,
що:
r |
r /2 |
|
r |
|
r |
|
; |
cos α cos60 1/2. |
|
|
2 cos 30 |
|
|
|
|||||
1 |
cos( /2) |
3 |
|
|
|||||
З урахуванням цього формула (2) набуде вигляду:
ДВНЗ «ДонНТУ»Автомобільно-дорожній інститут

82
Q4 Q1 / 
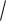 3.
3.
Зробимо обчислення:
Q4 10 9 / 
 3 Кл = 5,77 10 10Кл=577 пКл.
3 Кл = 5,77 10 10Кл=577 пКл.
Слід зазначити, що рівновага системи зарядів буде нестійкою.
Приклад 3. Два точкових електричних заряди Q1 1 нКл і Q2 2 нКл знаходяться в повітрі на відстані d 10 см один від одного.
Визначити напруженість E та потенціал поля, яке створене цими зарядами в точці A, віддаленої від заряду Q1 на відстань r1 9 см та від заря-
ду Q2 на r2 7 см.
Розв'язок. Згідно з принципом суперпозиції електричних полів, кожен заряд створює поле незалежно від присутності у просторі інших зарядів. Тому напруженість E електричного поля в точці, яку шукаємо може бути знайдена як геометрична сума напруженостей E1 та E2 полів, які створені кожним зарядом окремо: E E1 E2. Напруженості електрично-
го поля, яке створюється в повітрі ( 1) |
зарядами Q1 та Q2 : |
|||||||||
E |
|
|
Q1 |
|
|
; |
(1) |
|||
|
|
|
|
|||||||
|
|
|
|
|||||||
4 |
|
|
r2 |
|||||||
1 |
0 |
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|||
E |
|
|
Q2 |
|
|
|
. |
(2) |
||
|
|
|
|
|
||||||
|
|
|
|
|||||||
|
4 |
|
r2 |
|
||||||
2 |
|
|
|
|
|
|||||
|
|
|
|
|
0 |
2 |
|
|
|
|
Вектор E1 (рис. 8) спрямований по силовій лінії від заряду Q1, тому що цей заряд позитивний; вектор E2 направлено також по силовій лінії, але до заряду Q2 , тому що цей заряд негативний.
Рисунок 8 – Визначення вектора E у точці А
Методичний посібник та контрольні завдання з загального курсу фізики

Модуль вектора E знайдемо за теоремою косинусів: |
83 |
||||||||
|
|||||||||
|
|
|
|
|
|
|
|
|
|
E E2 |
E2 2E E |
2 |
cos α, |
(3) |
|||||
1 |
2 |
1 |
|
|
|
|
|||
де – кут між векторами E1 |
и E2 , який може бути знайдений з три- |
||||||||
кутника зі сторонами r1, r2та d : |
|
|
|
|
|
|
|
||
|
|
d2 r2 |
r2 |
|
|
|
|
||
cosα |
|
1 |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
2rr1 2
У даному випадку, щоб уникнути громіздких записів зручно значення cos обчислити окремо:
(0,1)2 |
(0,09)2 (0,07)2 |
||
cos α |
|
|
= – 0,238. |
|
|
||
|
|
2 0,09 0,07 |
|
Підставляючи вираз E1 з (1) і E2 |
з (2) в (3) та виносячи загальний |
||||||||||||||||||
множник 1/(4 0) за знак кореня, отримаємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
1 |
|
|
Q12 |
|
Q22 |
2 |
|
|
Q1 |
|
|
|
Q2 |
|
|
cos α. |
(4) |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
4 |
0 |
|
r4 |
r4 |
|
|
r2r2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
2 |
|
|
1 |
2 |
|
|
|
|
|
||||||
Відповідно до принципу суперпозиції електричних полів потенціал |
|||||||||||||||||||
результуючого поля, яке створене двома зарядами Q1 |
|
та Q2, |
дорівнює |
||||||||||||||||
алгебраїчній сумі потенціалів: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|||
Потенціал електричного поля, яке створене у вакуумі точковим зарядом Q на відстані r від нього, виражається формулою:
|
Q |
. |
(6) |
|
4 0r
У нашому випадку відповідно до формул (5) і (6) отримаємо:
Q1 Q2 4 0r1 4 0r2
або
ДВНЗ «ДонНТУ»Автомобільно-дорожній інститут

84
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Q |
Q |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
. |
|
|
|||||
|
|
|
|
|
4 |
0 |
|
r |
r |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
||||||
Зробимо обчислення: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Е |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
4 4 9 109 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
10 9 2 |
2 10 9 2 |
2 |
|
|
|
|
10 9 2 10 9 |
0,238 |
В м |
|||||||||||||||
0,09 4 |
|
0,09 2 |
0,07 2 |
||||||||||||||||||||||
|
|
|
0,07 4 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
3,58 103 В м 3,58 кВ м; |
|
||||||||||||||||||
|
|
|
|
1 |
|
10 9 |
|
|
2 10 9 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
–157 В. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
4 4 9 109 0,09 |
|
|
|
|
|
0,07 |
|
|
|
|
|
|
||||||||||
Приклад 4. По тонкому кільцю рівномірно розподілений заряд Q 40 нКл з лінійною щільністю 50 нКл/м. Визначити напруженість
E електричного поля, яке створене цим зарядом у точці А, що лежить на осі кільця й віддалена від його центру на відстань, рівну половині радіуса.
Розв'язок. Поєднаємо координатну площину xOy з площиною кільця, а вісь Oz– з віссю кільця (рис. 9).
|
Рисунок 9 – Визначення вектора E в точці А |
На |
кільці виділимо малу ділянку довжиною dl. Так як заряд |
dQ dl, |
що знаходиться на цій ділянці можна вважати точковим, то на- |
пруженість dE електричного поля, яке створене цим зарядом, може бути записана у вигляді:
Методичний посібник та контрольні завдання з загального курсу фізики
85
|
dl |
|
r |
|
|
dE |
|
, |
|||
|
|
||||
|
4 0r2 r |
||||
де r – радіус-вектор, спрямований від елемента dl до точки А. Розкладемо вектор dE на дві складові: dE1, перпендикулярно пло-
щині кільця (співнапрямлену з віссю Oz), і dE2 , паралельну площині кільця (площині xOy), тобто:
dE dE1 dE2.
Напруженість E електричного поля в точці А знайдемо інтегруван-
ням:
E E1 E2 ,
L L
де інтегрування ведеться по всіх елементах зарядженого кільця. Зауважимо, що для кожної пари зарядів dQ, та dQ'(dQ dQ'), розташованих
симетрично щодо центру кільця, вектори dE |
та dE' в точці А рівні по |
|
|
2 |
2 |
модулю й протилежні за напрямком: dE |
dE' . Тому векторна сума (ін- |
|
2 |
|
2 |
теграл) dE2 0. Оскільки складові dE1 |
для всіх елементів кільця співна- |
|
L |
|
|
прямлені з віссю Oz (одиничним вектором k ), тобто dE1 kdE1, тоді
E k dE1 .
L
Так як
dE dE cos α; |
|
|
|
dE |
dl |
; |
|
|
||
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
4 0r2 |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
r R2(R/ 2)2 |
|
|
R / 2; |
cos α (R /2)r 1/ |
|
|
||||
5 |
5, |
|||||||||
то
dE |
1 |
|
4 |
|
|
dl |
|
dl |
. |
|
|
|
|
|
|
|
|
|
|||
1 |
4 0 5R2 |
5 |
|
|
5 5 0R2 |
|
||||
ДВНЗ «ДонНТУ»Автомобільно-дорожній інститут

86
Таким чином:
|
2 R |
|
dl |
|
|
2 |
|||||
E k |
|
|
|
|
|
k |
|
|
|
. |
|
|
|
|
2 |
|
|
|
|||||
5 5 0R |
|
||||||||||
|
|
0 |
|
|
5 5 0R |
||||||
Зі співвідношення Q 2 R визначимо радіус кільця:
R Q / (2 ),
тоді:
|
|
2 2 |
|
4 2 |
||||||
E k |
|
|
|
k |
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||
|
|
5 5 0Q |
5 |
|
5 0Q |
|||||
Модуль напруженості:
|
|
|
|
4 2 |
|
|||
|
|
|||||||
E |
|
|
|
|
|
|
. |
(1) |
|
|
|
|
|
||||
|
|
5 |
|
5 0Q |
|
|||
|
|
|||||||
Перевіримо, чи дає права частина отриманої рівності одиницю напруженості (В/м):
|
2 |
|
(1 Кл/м) |
2 |
|
|
|
1 Кл |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 В/м. |
|
|||||
0 Q |
|
|
|
|
|
|
|
|
||||||||
|
1 Ф/м 1 Кл 1 Ф 1 м |
|
|
|||||||||||||
Виразимо фізичні величини, що входять до формули (1), в одиницях |
||||||||||||||||
СІ 5 10 8Кл/м, Q 4 10 8Кл, ε0 |
8,85 10 12Ф/м і зробимо |
обчис- |
||||||||||||||
лення: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
4 3,14 (5 10 8)2 |
|
В/м 7,92 кВ/м. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
5 5 8,85 10 12 |
4 10 8 |
|
||||||||||||
|
|
|
|
|
|
|
||||||||||
Приклад 5. Дві концентричні провідні сфери радіусами R1 6 см і |
||||||||||||||||
R2 10 см несуть відповідно заряди |
Q1 1 нКл і |
Q2 – 0,5 нКл. |
Знайти |
|||||||||||||
напруженість E поля в точках, віддалених від центру сфер на відстанях |
||||||||||||||||
r1 5 см, r2 9 см, r3 |
15 см. Побудувати графік E(r). |
|
||||||||||||||
Розв'язок. Зауважимо, що точки, в яких потрібно знайти напруже- |
||||||||||||||||
ності електричного поля, |
лежать у |
|
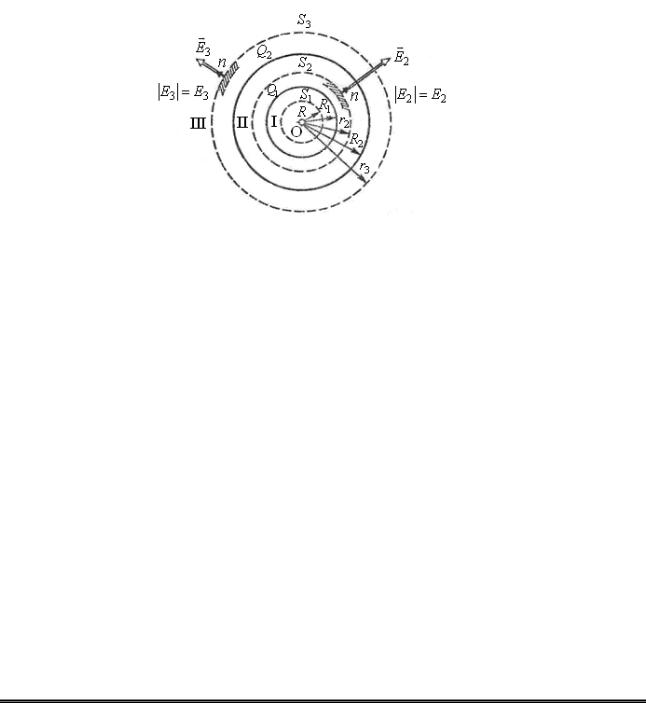
трьох областях (рис. 10): області |
|||||||||||||
I (r1 R1), області II(R1 < r2 < R2), області III (r3 > R2). |
|
|||||||||||||||
Методичний посібник та контрольні завдання з загального курсу фізики
87 1. Для визначення напруженості E1 в області I проведемо гауссову поверхню S1 радіусом r1 і скористаємося теоремою Остроградського –
Гауса:
E EndS 0,
S1
(оскільки сумарний заряд, що знаходиться всередині гауссової поверхні, дорівнює нулю). З міркувань симетрії En E1 const.
Відтак, E 0 та E1 (напруженість поля в області I) в усіх точках, які відповідають умові r1 R1, буде дорівнювати нулю.
Рисунок10 – Гауссові поверхні для двох концентричних сфер
2. В області II гауссову поверхню проведемо радіусом r2. В цьому випадку (діелектричну проникність ε середовища будемо вважати рівною одиниці (вакуум)):
E Q1 / 0,
(оскільки всередині гауссової поверхні знаходиться тільки заряд Q1). Так як En E const, то E можна винести за знак інтеграла:
E Q1 / 0 |
або |
ES2 Q1 |
/ 0 . |
Позначивши напруженість E для області II |
через E2 , отримаємо: |
||
E2 Q1 /( 0S2),
де S2 4 r22 − площа гауссової поверхні, тоді:
ДВНЗ «ДонНТУ»Автомобільно-дорожній інститут

88 |
Q1 |
|
|
||
E |
. |
(1) |
|||
|
|||||
2 |
4 |
r2 |
|
|
|
|
|
0 2 |
|
|
|
3. В області III гауссова поверхня проводиться радіусом r3. |
Позна- |
||||
чимо напруженість E області III через E3 та врахуємо, що в цьому випадку гауссову поверхню охоплює обидві сфери і, отже, сумарний заряд буде дорівнювати Q1 Q2, тоді:
E3 Q1 Q22 .
4 0r3
Помітивши, що Q2 0, цей вираз можна переписати у вигляді: |
|
|||||||
E |
Q1 |
|
Q2 |
|
|
. |
(2) |
|
|
|
|||||||
|
|
|||||||
|
|
|
|
|
||||
3 |
4 |
|
|
r2 |
|
|||
|
|
0 3 |
|
|
|
|
||
Переконаємося в тому, що права частина рівності (1) і (2) дає одиницю напруженості:
|
|
Q |
|
|
|
|
1 Кл |
|
1 Кл |
1 В/м. |
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 Ф/м 1 м2 |
|
|||
|
|
|
|
|
|
|||||||
|
0 |
|
r2 |
|
|
|
1 Ф 1 м |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Виразимо |
всі |
|
|
|
|
величини |
|
в одиницях |
|
СІ |
(Q 10 9 Кл; |
||||||||||||||||||
Q 0,5 10 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
Кл; |
r |
0,09 м; |
|
r |
0,15 м; 1/(4 |
0 |
) 9 109м/Ф) |
|
та зро- |
||||||||||||||||||||
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
бимо обчислення: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
E |
|
|
|
|
|
|
|
|
9 |
|
109 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
9 10 |
|
|
|
|
|
В/м 1,11 кВ/м; |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
(0,09)2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
E |
|
|
|
|
|
|
|
|
9 |
|
(1 0,5)10 9 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
9 10 |
|
|
|
|
|
|
|
В/м 200 В/м. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
(0,15)2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Побудуємо графік |
E(r). |
В області I (r1 R1) |
E 0. |
В |
|
області |
|||||||||||||||||||||||
II (R r R ) E (r) |
|
|
змінюється за законом 1/ r2 . У точці r R |
|
напруже- |
||||||||||||||||||||||||
1 |
|
2 |
2 |
|
|
|
|
|
|
|
R2) 2,5 кВ/м. У точці |
|
|
|
|
1 |
|
|
|
||||||||||
ність |
E (R ) Q /(4 |
0 |
r R |
( r |
прагне до R |
||||||||||||||||||||||||
|
2 |
1 |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|||
зліва) |
E (R ) Q /(4 |
0 |
R2) 0,9 |
кВ/м. В області |
III (r R ) |
E (r) змі- |
|||||||||||||||||||||||
|
2 |
2 |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
нюється за законом 1/ r2 , причому в точці r R |
(r прагне до R |
|
право- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
||
руч) |
E (R ) (Q |
|
Q |
|
)/(4 |
0 |
R2) 0,45 кВ/м. |
Таким |
чином, |
|
функція |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
3 |
2 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
E(r) у точках r R1 |
|
|
та r R2 зазнає розрив. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методичний посібник та контрольні завдання з загального курсу фізики

89
Графік залежності Er представлений на рис. 11.
Рисунок 11 – Графік залежності E(r)
Приклад 6. Точковий заряд Q 25 нКл перебуває в полі, яке створене прямим нескінченним циліндром радіусом R 1 см, рівномірно зарядженим з поверхневою щільністю 0,2 нКл/см2. Визначити силу F , яка діє на заряд, якщо його відстань від осі циліндра r 10 cм.
Розв'язок. Значення сили F , яка діє на точковий заряд Q, що знаходиться в полі, визначається за формулою:
F QE, |
(1) |
де E – напруженість поля.
Як відомо, напруженість поля нескінченно довгого рівномірно заря-
дженого циліндра: |
|
|
|
E |
|
, |
(2) |
|
|||
|
2 0r |
|
|
де – лінійна щільність заряду. |
. Для |
||
Виразимо лінійну щільність через поверхневу щільність |
|||
цього виділимо елемент циліндра довжиною l і виразимо заряд, |
що зна- |
||
ходиться на ньому Q, двома способами: Q S 2 Rl; Q l Прирівнявши праві частини цих формул і скоротивши отриману рівність на l, знайдемо 2 R . З урахуванням цього формула (2) набуде вигляду: E R /( 0r). Підставивши вираз E в (1), отримаємо:
F Q R.
0r
Зробимо обчислення:
ДВНЗ «ДонНТУ»Автомобільно-дорожній інститут
90
F 2,5 10 8 2 10 6 1 Н 5,65 10 4Н 565 мкН. 8,85 10 12 10
Сила F співнапрямлена з напруженістю E, яка в силу симетрії (циліндр нескінченно довгий) перпендикулярна поверхні циліндра.
Приклад 7. По тонкій нитці, яка зігнута по дузі кола, рівномірно розподілений заряд з лінійною щільністю 10 нКл/м. Визначити напруженість E та потенціал електричного поля, яке створене таким розподіленим зарядом у точці, яка співпадає з центром кривизни дуги. Довжина l нитки становить 1/3 довжини кола й дорівнює 15 см.
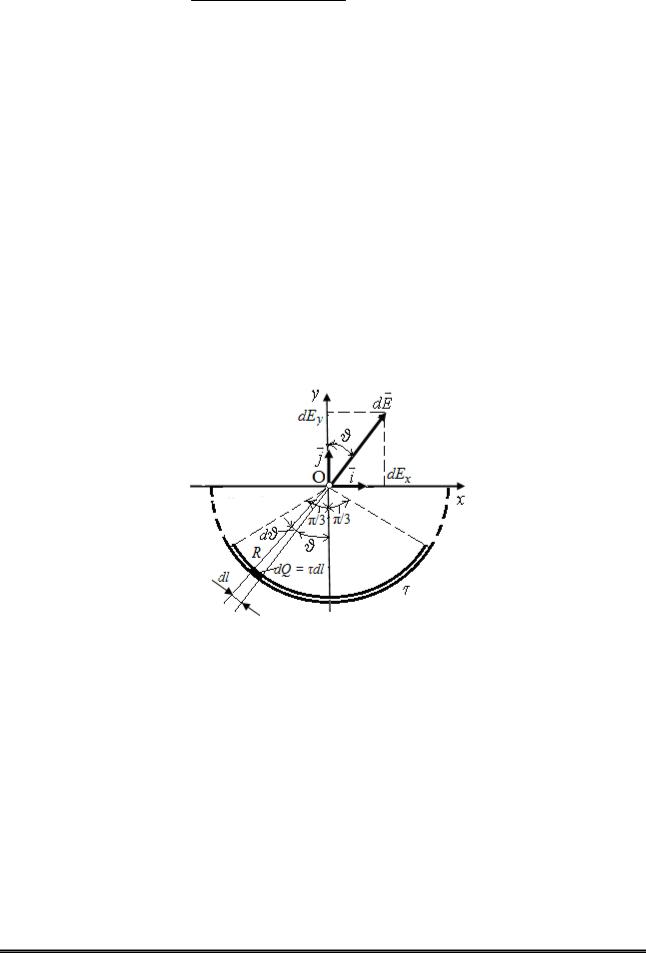
Розв'язок. Виберемо осі координат так, щоб початок координат співпадав з центром кривизни дуги, а вісь Oy була б симетрично розташована щодо кінців дуги (рис. 12). На нитці виділимо елемент довжини dl. Заряд dQ dl, що знаходиться на виділеній ділянці, можна вважати точковим.
Рисунок 12 – Напруженість dE поля, яке створене зарядом dQ
Визначимо напруженість електричного поля в точці O. Для цього знайдемо спочатку напруженість dE поля, створюваного зарядом dQ:
|
dl |
|
r |
|
|
dE |
|
, |
|||
|
|
||||
|
4 0r2 r |
||||
де r – радіус-вектор, спрямований від елемента dl до точки, в якій обчислюється напруженість.
Виразимо вектор dE через проекції dEx і dEy на осі координат:
Методичний посібник та контрольні завдання з загального курсу фізики
