
КДМ, ч2(5-7)
.pdf
|
|
|
|
31 |
Толщина G − |
этоминимальноечисегоп анарныхподграфов, |
|
||
|
объединениекоторыхдаетисходныйграф |
G (о бозначают |
||
|
t(G)). |
|
|
|
Родграфа |
G − этоминимальнкоторыечислоручек, не бходимо |
|
||
|
добавитьксфере,чтоможнобыулографжить |
G без |
||
|
самопересечений, ребер. |
|
||
Непланарныйг |
раф, |
укладывающийся |
наторебезп ресечений |
|
|
самопересеченийреберназываются |
тороидальными,род |
||
|
такогографаравен1. |
|
|
|
Ктороидальнымграфам |
|
относят графы K5 , K7 , K 3,3 , K4, 4 . |
||
Примерукладыванияграфа |
|
K 3,3 наторе: |
|
|
|
|
Заданиек |
лабораторнойработе |
|
|
Исходданграфные |
G : GV(13, {5, 6}) . |
|
|
||
1. |
Определить,яв яется |
исходный граф G планарным или |
|||
непланарным,используякритерийПонтрягина |
-КуратовскогоилиВагнера. |
|
|||
Найтиподграф |
|
G ,гомеоморфный K 5 или K 3,3 |
покритериюПонтрягина |
- |
|
Куратилипо,стягиваемыйдграфвского |
K 5 |
или к K 3,3 покритерию |
|
||
Вагнера. |
|
|
|
|
|
2. |
Еслиисходныйграфпланарен,обозначитьего |
|
G1. |
|
|
|
|
|
|
|
|
32 |
3. |
Еслиисходныйграфнепланарен |
|
, обозначитьего |
G2. |
|
|
4. |
Еслиисходныйграфбылпланарен |
|
, |
добавитьминимальное |
|
|
числоребдонепланарности |
иобозначитьполученныйнепланарныйграф |
|
|
|
||
G2. |
|
|
|
|
|
|
5. |
Если исходныйграфбылнепланарен |
, |
удалитьминимальное |
|
||
числореберобозначитьполучепланграрныйф |
|
|
G1. |
|
|
|
6. |
Количестводобавляемыхудаляемых( )припреобразованиях |
|
|
|
||
графаребердолжнобытьобосновано. |
|
|
|
|
|
|
7. |
Построитьплоскуюукладкуграфа |
|
G 1,используяалгоритм |
γ . |
||
Продемонстрироватьпошаговоевыполнениеалгоритма |
|
|
γ . |
|
|
|
8. |
Длянепланарногографа |
|
G2 найтирод,толщину,искаженность |
|
|
|
ичислоскрещиваний. |
|
|
|
|
|
|
Контрольныевопросы
1.Какойграфназываетсяплоским,планарным?
2.ЧтотакжокриваярданСформулироватье? теорему
Жорданоиследствиеизнее.
3.Датьопределениеграниграницы.
4.Какиеграниназываютвнутр? е?ннимишними
5.СформулиртеоремуЭйдплераяграфаоскогов. ть
6.Операцазбипод еберстягиванияе.ршин
Гомеоморфныеграфы.
7. СформукритериипланарностиирП нтрягвать на -
КуратовскогоиВагнера.
8.Алгоритмплоскойукладкиграфа.Опрседелениегмента,
контактнойвершины, |
α − цепи, |
допустимой грани. |
|
9. |
Характенепланарныхг ,истикиродафов,толщина,число |
|
|
скрещиванийискаженность. |
|
|
|
33
Лабораторнаяработа№7
Раскраскаграфов
Цельработы: приобретенпрактическихнавыковопределения
хроматичиндслаескогокса |
для неорграфов,построении |
оптимальной |
субоптимальнойправильнойвершиннойребернойраскраскиграфов.
|
|
Теоретическаясправка |
|
|
|
|
|
|
Вершиннаяраскраскаграфов |
|
|
|
|
|
− простой неориентированныйграф, |
|
− натурачис. льное |
|||
Вершинной |
k-раскраской илипросто |
k-раскраской |
графа G называется |
|||
= ( , ) |
|
|
|
|
||
|
|
произвольнаяфункция |
f, отображающаямножествовершин |
|
||
графа G внекоторое k-элемножествоентное:
: |
v |
|
{ |
|
|
, G, … , |
}=A. |
|
||
|
VG → |
|
|
|
|
|
||||
Есднекоторойлиявершины |
|
графа |
: f(v)=i, тоговорятчтовершина |
v |
||||||
раскрашенавi |
-тыйцвет . |
|
|
|
|
|||||
Раскраска называется правильной,если |
|
f(u) ≠ f(v) длюбыхясмежных |
||||||||
вершин u и v графа G (иликонцевыевершинылюбогоребра |
|
|||||||||
окрашенывразныецвета). |
|
|
|
|
|
|
|
|
|
|
Граф,длякоторогосуществуетправильная |
|
|
|
|
|
|
|
|
k-раскраска,назыв ется |
k- |
раскрашиваемым. |
|
|
|
|
|
|
|
|
||
Хроматическоечислографа |
|
G − этоминимальноечислокрасок,при |
|
|||||||
которомграфимеетправильнуюраскраску. |
|
|
|
|
|
|
|
|
|
|
Еслихроматическоечислоравно |
|
|
k,тографназы |
|
вается k-хроматическим |
|||||
(обозначают χ(G) = k). |
|
|
|
|
|
|||||
Правильную k-раскраску графа G можнорассмкакзбтриениевать |
|
|||||||||
множествавершинграфа |
|
|
|
|
|
|
G нанеболеечем |
k непустых |
||
множеств,которназываютсяе |
цветнымиклассами |
. |

|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
||
|
|
|
|
|
Графысмалымхро числоматическим |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Леммао2 |
-храскрашиваемыхграфах |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пусть – простойнеориентированныйграф |
|
: |
|
! ! = |
|
|
|
|||||||||
) ( ) = |
тогдаитолькотогда,когда |
|
|
− пустойграф, |
. |
|
|
|||||||||
) ( ) = |
тогдаитолько |
тогда,когда |
|
|
|
( ) = |
|
|
|
|
|
|||||
|
|
|
|
− непустдвудграф.ольный |
|
. |
|
|
|
|
||||||
|
|
Еслинепустойграфявляетсядеревом,то |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Леммаораскраскециклов |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Хроматическоечив лоциклаяксодержащего, |
|
|
|
p вершин, |
|
|
|
|||||||
|
|
|
|
равно 2, если p − четно,и3,если |
p − нечетно. |
|
|
|
|
|
|
|||||
|
|
Еслиграф |
|
G содержитциклнечедлины, о ой |
|
|
|
( ) > . |
|
|
|
|||||
|
|
|
|
|
Леммаораскраскеполногографа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Хроматическоечисло |
полного графа |
|
равно p. |
|
|
|
|
|
|||||
|
|
Еслиграф |
|
то ( ) |
≥ . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
G содержитподграф |
|
|
|
|
|
|
, |
|
|
|
|
Граф,укоторого |
|
χ = 2 , называются бихроматическим. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ТеоремаКёнига |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Непустойграфявляется |
бихроматическим тогдаитолькотогда, |
|
|
|
|
|
|
|||||||
|
|
|
|
|
коннегдасодержитцикловнечедлины. ой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следствие1. Людеревобоеихроматично.
Следствие2. Любойдвудольныйграфбихроматичен.
|
|
Оценкихроматического |
числаграфа |
|
|
|
|
|
Под нижнимиоценкамихроматическогочисла |
|
|
|
понимают |
||||
неравенствавида |
: |
|
,где c − некоторвычисляемаянст, апонта |
|
|
|
||
графу G ,апод |
верхними |
− неравенства |
вида |
|
|
, где c |
||
|
|
≥ оценками |
|
|
≤ |
|||
иметотжесмысл.т |
|
|
|
|
|
|
||

|
|
|
|
|
|
|
|
|
35 |
|||
|
|
|
Перваянижняя |
|
оценка |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
Дляпроизвольногографа |
|
= ( , ), | | = , | | = |
|
|
|
|
|||||
|
|
справедливонеравенство |
|
|
|
|
||||||
|
|
|
|
|
|
( ) ≥ ! |
|
|
|
|
|
|
|
|
Хроматическоеплотностьграфа |
|
|
|
или |
|
|
|
|
||
|
|
вторая нижняяоценка |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Дляпроизвольногографа |
|
|
G справедливонеравенство |
|
|
|
|
|
||
|
( ) ≥ ( ), где ( ) − плотностьграфаиликликовчислое |
|
|
|
|
|
||||||
|
|
Теографбезематреугольниковх |
|
|
|
|
|
|
||||
|
Дляпроизвольного |
≥ |
|
|
( ) = и ( ) |
= |
|
|
|
|
||
|
|
|
|
|||||||||
|
|
сущепростойвязныйтвуетграф |
|
|
|
|
|
|||||
|
|
такой,что |
справедливо |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
Хроматическоечислонезавграфалимости |
|
|
|
|
|
|
|
|
|
||
|
|
|
третья нижняяоценка |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
Дляпроизвольногографа |
|
G справедливонеравенство |
|
: |
|
|
|
||||
|
|
( ) ≥ ( ), где ( ) − числонезависимости |
графа |
|
|
|
|
|||||
|
|
Вероценкихроматическогониечисла |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
Дляпроизвольногографа |
|
G справедливонеравенство |
|
: |
|
|
|
||||
|
( ) ≤ ( ) + , где ( ) − максимумизстепенейвершин |
|
графа |
|
|
|
||||||
|
|
|
ТеоБруксаема |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
Для |
связннеполного |
|
графа G приусловии,что |
. ( ) ≥ , |
|
||||||
|
справедливонеравенство |
|
: |
( ) ≤ ( ) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечаниеокомпонентахсвязности |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Хроматическоечислографаравноксимумуиз |
|
|
|
|
|
|
|
|
||
|
|
хроматическихчиселегомпонентсвязности |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|

36
Гипокраскахырехеза
любогопланарного графа
4
Теорема
любогопланарного графа
5
|
п |
|
(субоптимальный |
|
||
1. |
графа |
|
приписываем. |
|
|
|
2. |
Пустьраскрашены |
вершинграфа |
вцвета |
1 |
k,где |
|
k ≤ i. |
|
|
|
! |
приписываем |
|
|
неиспользованный |
а краске |
|
сней |
||
вершин. |
последовательной |
|
вы |
|
|
бора |
вершин |
|
|
|
|
|
|
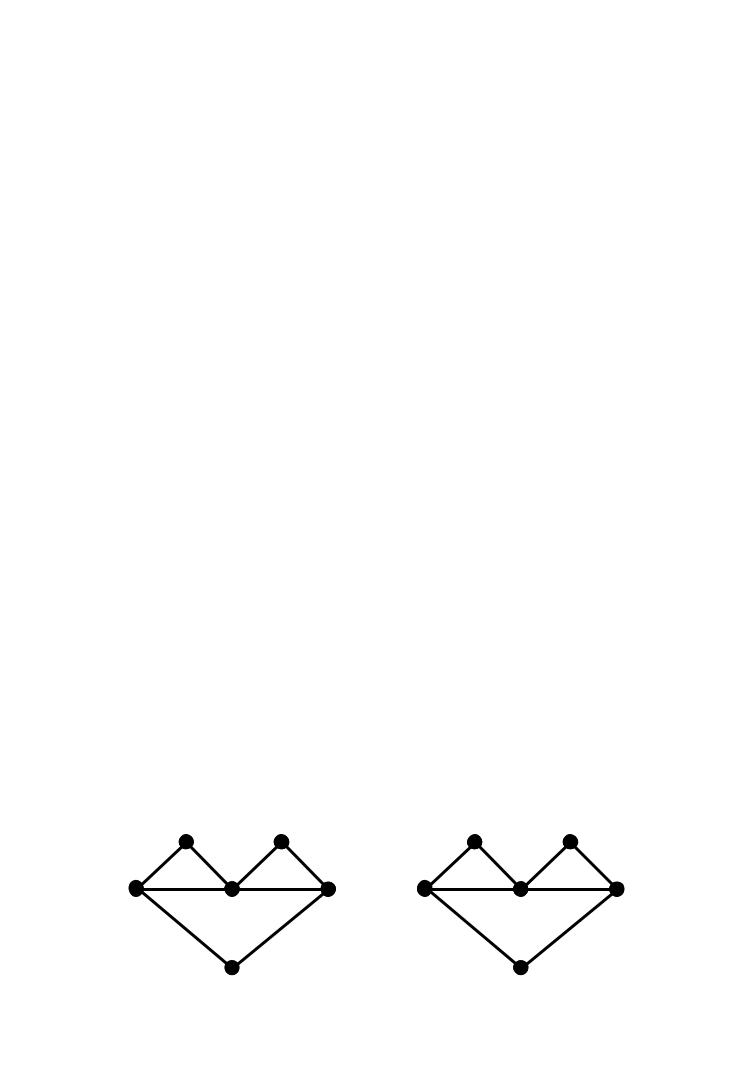
Напри
|
Впервом |
вершинградлфая |
|
|
|
|
: |
|
b, |
.Число, |
|
|
|
правильной раскграфааски,равно |
|
|
|
|
||
|
2 |
|
2 |
c |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
f |
|
|
g |
g |
втором |
оследовыбоатерадлраскраскиь ость |
|
|
(a, b, d, |
g) |
,и |
правильнойраскраски |
вершинграфа, 3.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |
||||
|
раскраска |
|
|
|
|
|
|
|
, i, j |
|
графа G V, |
|
V |
|
|
, |
|
E |
|
= q, c |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
матрицейсмежности |
|
|
|
|
|
aij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
p, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
пере |
|
|
|
вершин. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аибольшие − |
» |
|
|
|
|
|
или |
|
упорядочение |
|
|
|
|
|
||||||||||
Упорядочиваемвершиныграфа |
|
|
|
|
|
|
G впоряд |
|
возрастаниястепеней |
||||||||||||||||||
deg |
i ) . |
|
|
|
|
|
|
|
|
|
графа G |
|
последовательной |
|
|
|
|
|
|||||||||
раскраски, изсписка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеют |
||||||||||
степенидвухшаговыепени |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
deg |
vi ) |
маршрут2,и |
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vi итак |
||||||
.Рекурдляропределенияентнаямула |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
степени |
|||||||
вершиныграфа |
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
gk |
) = |
aij |
eg |
|
|
v |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
j ) |
|
p. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Последними |
|
|
|
|
|
|
|
» илиПН |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
в графесна |
еипенью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
номер |
|
|
.Удаляемэтусовсемией |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ребрами.Вполученномнаходимв |
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
номер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Например: |
(d, |
b, |
, g) |
|
|
|
|
|
|
|
|
d, |
b, a, g) |
||||||||||||||
НП- |
|
|
|
|
|
- |
|
|
|||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
c |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
f |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
g |
g |
|
|
|
|
|
|
38 |
|
|
Раскраска |
ребернаяраскраска |
|
|
|
Пуесть |
|
G = |
| V | |
| E | = q. |
|
|
Реберной |
k |
|
|
называется |
|
ϕ , |
|
|
отображение |
множества реберграфа |
в некоторое k- |
||
|
|
множество |
,т. е. ϕ : E → |
{a1,..., ak } |
||
Если ϕ(e) = |
,что |
|
e окрашеновцвет |
c. |
|
|
Реберная |
|
|
|
правильной,е лиребра |
|
|
|
|
в . |
|
|
|
|
Граф G называется k |
|
,еслиуществуетправильная |
k- |
|||
|
|
ребер. |
|
|
|
|
число |
|
|
существуправильнаяребернаят |
|
k- |
|
|
|
называется |
ребернымхроматическимчислом |
или |
||
|
|
|
индексом. |
|
|
|
Граф G |
называется |
|
- |
хроматический |
||
|
|
равен |
k: χ! |
) = k. |
|
|
Множреб,окрашенстворопред ыхленный |
|
|
|
|
||
K3 |
2 |
a |
2 |
b |
1 |
3 |
1 |
|
1 |
1 |
2 |
3 |
c |
d |
|
|
|
|

|
|
|
|
|
39 |
Хроматическийиндекс |
|
графасчетнымчисломверш |
ин |
||
равен: |
χʹ(K2n ) = 2n − 1 исне етным |
ʹ(K2n+1 ) = 2n + 1. |
|||
Примерможно |
проиллюстрировать: |
|
|||
|
|
K4 |
a |
3 |
b |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
c |
|
d |
|
|
|
3 |
||
|
Задклабораторнойние |
|
|
|
Исходданграфные |
G (13, {5, 6}). |
|
||
1) |
Планграфрный |
работы№6 |
|
обозначить G1 |
(исходныйилипреобразованный), |
а непланарный − G |
|
||
2) |
Вычислить ипроанализировать |
для плаинепланарного |
||
графов верхниенижниеоц нкичисла. |
|
|
|
|
3) |
Последовраскраситьграфтельно |
ы G и |
G2, используя |
|
алгоритм последовательнойраскраски,модификацииалгоритмаНП |
|
- и |
||
ПН-упорядочевершинием |
. |
|
|
|
4) |
Найти хроматическоесло |
хроматическийиндекс |
графов G1 |
|
и G2. Ответобосновать. |
|
|
|
|
5) |
Сравнитьхроматическоечислографов |
и G2 соценками, |
||
полученнымианалитвзадан2врезультатеческипр трм нениях |
|
|
|
|
алгоритм,взадании3Пр. оанавполученныеизировать |
|
результаты. |
||
6) Привестипримерграфа,укоторогочислокрасокзависеть
отпорядкаобходавершин.
40
Контрольныевопросы
1.Вершиннаяаскрасканеориентированныхграфов
2.Какаяраскрасканазываетсяправильной?
3. |
Длякакихграфовмогутбытьпримененыалгоритмы |
раскраски? |
4.Какойграфназываютправильнораскрашенным?
5.Чтоназываетхроматическимчиграфа?ялом
6.Нижниеоценкихроматическогочислаграфа.
7.Вероценкихниероматическогочислаграфа.
8.Определениецветногокласса.
9. |
СформулироватьтеоремуКенига |
. |
10. |
Сформулироватьгипоче пятиырехезу |
красок. |
11. |
Алгпоследовательнойритм |
вершинной раскраскиграфов . |
12.Последовательныеметодыраскрашива,основанна нияые
упорядочении множествавершин. |
НПиПН -упорядочениевершин. |
|
13. |
k-шаговаястепеньвершины |
рекурформулаеентная |
вычисления. |
|
|
14.Ребернраскраскаилияскраскаребер.
15.Правильреберраскраска,реберныйнаяцветнойкласс.
16.Опреберногоеделенхроматическогоилисла
хроматическогоиндекса.
17.Хроматическийиндексполныхграфов.
