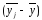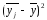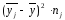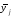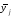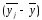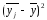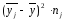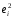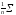Таблиця 3.64 – Розрахунки міжгрупової дисперсії

Групові середні,
63,39	-18,17	330,15	660,3
74,57	-6,99	48,86	293,16
76,81	-4,75	22,56	112,81
83,89	2,33	5,43	32,57
99,16	17,6	309,76	1548,8
Разом			2647,64

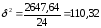
Якщо підставити розраховані показники отримаємо F-критерій Фішера:

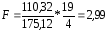
Критичний показник для рівня істотності  = 0,05 складає F_0,05=2,9. Розрахований Критерій Фішера перевищує критичний, а отже зв’язок між фондоозброєністю та продуктивністю праці робітника з імовірністю 0,954 визнається істотним.

Таблиця 3.71 – Розрахунки для відбору факторів, що впливають на вихідний показник

№ групи	Значення границь груп за плинністю кадрів	Кількість елементів у групі (обсяг групи) nj	Значення показників у, які відповідають елементам групи	Групові середні
1	2,1 – 5,4	4	90,9; 90,7;113,7;100,1	98,85
2	5,4 – 8,7	4	89,0; 85,7; 79,7; 85,3	84,93
3	8,7 – 12,0	9	75,8; 80,7; 71,0; 72,7; 72,9; 80,5; 101,9; 102,5; 103,8	84,64
4	12,0 – 15,3	4	62,8; 68,6; 73,7; 83,4;	72,13
5	15,3 – 18,6	3	57,8; 62,5; 59,8	60,03
Разом		24

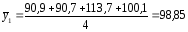грн./люд-годину

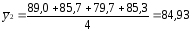грн./люд-годину

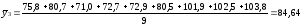грн./люд-годину

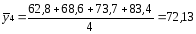грн./люд-годину

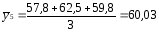грн./люд-годину

Центром розподілу сукупності в цілому є загальна середня:

81,9 грн./люд-годину

Проведемо перевірку істотності зв'язку для плинності кадрів.

Таблиця 3.72 – Розрахунки міжгрупової дисперсії

Групові середні,
98,85	17,29	298,94	1195,78
84,93	3,37	11,36	45,43
84,64	3,08	9,49	85,38
72,13	-9,43	88,92	355,70
60,03	-21,53	463,54	1390,62
Разом			3072,90

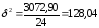
Якщо підставити розраховані показники отримаємо F-критерій Фішера:

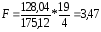
Розрахований показник перевищує критичний F_0,05=2,9, тому зв'язок між продуктивністю праці і плинністю кадрів з імовірністю 0,954 визнається істотним.

Надалі проведемо дослідження однофакторного зв'язку. Рівняння регресії будемо досліджувати у вигляді Y=| (де Y — розрахунковий (теоретичний) рівень результативної ознаки).

Розрахунок коефіцієнтів рівняння можна здійснити за формулами

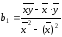(3.2)

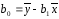
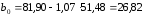
Таким чином, рівняння регресії має вигляд Y=26,82+1,07x. Для проведення розрахунків скористаємось таблицею

Таблиця 3.81 – Розрахункова таблиця для визначення параметрів однофакторного зв'язку та їхньої оцінки

№ з/п
1	2	3	4	5	6	7	8	9	10	11
1	29,00	57,80	841,00	3340,84	1676,20	57,85	-0,05	0,00	-24,05	578,20
2	48,20	62,80	2323,24	3943,84	3026,96	78,39	-15,59	243,17	-3,50	12,26
3	40,60	62,50	1648,36	3906,25	2537,50	70,26	-7,76	60,25	-11,63	135,35
4	38,40	59,80	1474,56	3576,04	2296,32	67,91	-8,11	65,74	-13,99	195,66
5	40,50	75,80	1640,25	5745,64	3069,90	70,16	5,65	31,87	-11,74	137,85
6	33,20	68,60	1102,24	4705,96	2277,52	62,34	6,26	39,14	-19,55	382,27
7	41,80	80,70	1747,24	6512,49	3373,26	71,55	9,15	83,80	-10,35	107,12
8	46,80	73,70	2190,24	5431,69	3449,16	76,90	-3,20	10,21	-5,00	25,00
9	54,60	71,00	2981,16	5041,00	3876,60	85,24	-14,24	202,83	3,35	11,20
10	52,50	72,70	2756,25	5285,29	3816,75	83,00	-10,30	105,99	1,10	1,21
11	58,30	89,00	3398,89	7921,00	5188,70	89,20	-0,20	0,04	7,31	53,37
12	40,50	72,90	1640,25	5314,41	2952,45	70,16	2,75	7,54	-11,74	137,85
13	40,40	80,50	1632,16	6480,25	3252,20	70,05	10,45	109,24	-11,85	140,37
14	48,50	83,40	2352,25	6955,56	4044,90	78,72	4,69	21,95	-3,18	10,12
15	47,40	85,70	2246,76	7344,49	4062,18	77,54	8,16	66,62	-4,36	18,99
16	58,70	101,90	3445,69	10383,61	5981,53	89,63	12,27	150,58	7,73	59,80
1	2	3	4	5	6	7	8	9	10	11
17	64,30	90,90	4134,49	8262,81	5844,87	95,62	-4,72	22,29	13,73	188,38
18	56,70	79,70	3214,89	6352,09	4518,99	87,49	-7,79	60,67	5,59	31,28
19	61,60	90,70	3794,56	8226,49	5587,12	92,73	-2,03	4,13	10,84	117,42
20	62,10	85,30	3856,41	7276,09	5297,13	93,27	-7,97	63,47	11,37	129,30
21	70,90	113,70	5026,81	12927,69	8061,33	102,68	11,02	121,37	20,79	432,11
22	68,30	100,10	4664,89	10020,01	6836,83	99,90	0,20	0,04	18,01	324,19
23	66,90	102,50	4475,61	10506,25	6857,25	98,40	4,10	16,79	16,51	272,49
24	65,20	103,80	4251,04	10774,44	6767,76	96,58	7,22	52,07	14,69	215,74
	1235,40	1965,50	66839,24	166234,23	104653,41	1965,56	-0,06	1539,79	0,06	3717,52
	51,48	81,90	2784,97	6926,43	4360,56	81,90	0,00	64,16	0,00	154,90

Необхідно побудувати кореляційне поле за емпіричними (вихідними) даними та «наложити» на нього лінію регресію, що побудована за визначенним рівнянням регресії, що дозволяє зробити попередні висновки про відповідність рівняння вихідним даним.

Рисунок 3.7 – Кореляційне поле взаємозв’язку між продуктивністю праці та фондоозброєністю

Вплив та напрямок однофакторного зв'язку характеризує лінійний коефіцієнт кореляції, який можна визначити за формулою 2.9б.

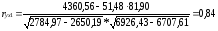
Позитивне значення r означає прямий зв'язок між ознаками. Прийнято вважати, що при r0,7 зв'язок між ознаками сильний. Показником тісноти зв'язку між результативною та факторною ознакою є коефіцієнт детермінації (множинної кореляції) (див. формулу 2.97а)

Порівняємо коефіцієнт кореляції та коефіцієнт детермінації.

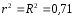
Це свідчить про лінійний зв'язок між х та у. Тобто продуктивність праці змінюється пропорційно зміні фондоозброєності. Розрахуємо коефіцієнт кореляції між продуктивністю праці і плинністю кадрів.