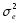- •2 Методологічні основи статистичного аналізу соціально-економічних явищ і процесів
- •Більш широко використовується середня гармонічна зважена:
- •3 Статистичний аналіз показників діяльності підприємства
- •3.1 Побудова рядів розподілу економічних показників та визначення їх основних статистичних характеристик
- •Таблиця 3.64 – Розрахунки міжгрупової дисперсії
- •Таблиця 3.72 – Розрахунки міжгрупової дисперсії
- •Таблиця 3.81 – Розрахункова таблиця для визначення параметрів однофакторного зв'язку та їхньої оцінки
- •Таблиця 3.82 – Розрахункова таблиця для визначення параметрів однофакторного зв'язку та їхньої оцінки
- •Таблиця 3.92 – Розрахункова таблиця для визначення параметрів багатофакторного зв'язку та їхньої оцінки
Більш широко використовується середня гармонічна зважена:
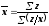 ,
z
= x
f
(4.1) (2.43)
,
z
= x
f
(4.1) (2.43)
де Zj = xj fj — обсяг значень ознаки (у нашому прикладі — вартість).
Якщо визначальна властивість сукупності формується як добуток індивідуальних значень ознаки, використовується середня геометрична:
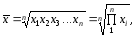 (2.44)
(2.44)
де П — символ добутку;
xі — відносні величини динаміки, виражені кратним відношенням j-го значення показника до попереднього (j – 1)-го.
Коли часові інтервали не однакові, розрахунок виконують за формулою середньої геометричної зваженої:
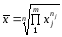 , (2.45)
, (2.45)
де nj — часовий інтервал,
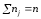 ,
,
m — кількість інтервалів.
Також можливе застосування степеневої середньої. Окремим випадком степеневої середньої э квадратична середня:
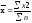 (2.46)
(2.46)
По суті це перетворена середня арифметична. Її використовують тоді, коли показник, виступаючий вагами f, відсутній та його слід додатково визначати на підставі відомих варіант х і множення варіант на частоту хf.
При розрахунку показників варіації використовують або модулі, або квадрати відхилень. Тому використовують характеристики варіації: середнє лінійне l та середнє квадратичне відхилення та дисперсію 2 (див. таблицю 2.2)
Таблиця 2.2 - Розрахунок узагальнюючих характеристик варіації
|
Показник |
Середнє відхилення | |
|
лінійне |
квадратичне | |
|
За даними: - незгрупованими |
|
|
|
- згрупованими |
|
|
Очевидно, що дисперсія – це середній квадрат відхилень.
Середнє
лінійне
 та середнє квадратичне
та середнє квадратичне відхилення є безпосередніми мірами
варіації. При порівнянні варіації різних
ознак або варіації однієї ознаки в
різних сукупностях використовують
відносні характеристики - коефіцієнти
варіації:
відхилення є безпосередніми мірами
варіації. При порівнянні варіації різних
ознак або варіації однієї ознаки в
різних сукупностях використовують
відносні характеристики - коефіцієнти
варіації:
- лінійний
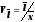 ;
(2.51)
;
(2.51)
- квадратичний
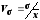 ; (2.52)
; (2.52)
- осциляції
 ;
(2.53)
;
(2.53)
- квартильний
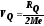 (2.54)
(2.54)
Для оцінки однорідності сукупності та порівняння варіацій найбільш часто використовують квадратичний коефіцієнт варіації. В економічних розрахунках вважають, що сукупність є однорідною, а середня - типовою, якщо коефіцієнт варіації не перевищує 10-15% (в математиці ця величина складає 33%).
Середній квадрат відхилення 2 або дисперсія посідає особливе місце у статистичному аналізі соціально-економічних явищ. Вона є невіддільним і важливим елементом інших статистичних методів, зокрема дисперсійного аналізу. є невіддільним і важливим елементом інших статистичних методів, зокрема дисперсійного аналізу. Залежно від даних вона може бути простою та зваженою:
- для незгрупованих даних
 (2.61)
(2.61)
- для згрупованих
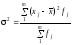 (2.62)
(2.62)
Більш зручно проводити розрахунки дисперсії за формулою різниці квадратів:
 (2.63)
(2.63)
де
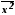 -
середній квадрат значень варіюючої
ознаки;
-
середній квадрат значень варіюючої
ознаки;
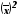 - квадрат
середньої величини.
- квадрат
середньої величини.
Перетворена формула дисперсії (5.13) має наступний вигляд:
- для незгрупованих даних
 ; (2.64)
; (2.64)
- для згрупованих даних
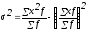 ; (2.65)
; (2.65)
Дисперсія альтернативної ознаки обчислюється як добуток часток:
 , (2.66)
, (2.66)
де
 — частка елементів сукупності, яким
властива ознака,
— частка елементів сукупності, яким
властива ознака,
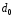 —частка
решти елементів
—частка
решти елементів
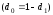 .
.
За відсутності варіації 2=0. Максимальне значення дисперсії складає 0,25, коли d1 = d0 = 0,5, а саме, коли одиниці сукупності порівну розподілені між двома значеннями.
У тому випадку, коли номінальна ознака приймає не два, а більше значень дисперсія розраховується за формулою
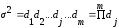 (2.67)
(2.67)
де dj - частка j-й групи;
m - кількість груп.
Практично дисперсія розраховується по спрощуючій обчислення формулі, званій «відліком від умовного нуля»:
 (2.68)
(2.68)
де k й х0 - довільні постійні.
Якщо сукупність розбито на групи за певною ознакою х, то для будь-якої іншої ознаки у можна обчислити дисперсію як у цілому по сукупності, так і в кожній групі. Центром розподілу сукупності в цілому є загальна середня
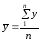 або
або
 (2.71)
(2.71)
центром розподілу в j-й групі — групова середня
 або
або
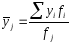 (2.72)
(2.72)
де fj = fi - обсяг групи j.
Загальна дисперсія характеризує варіацію ознаки у навколо загальної середньої:
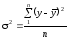 або
або
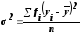 (2.73)
(2.73)
Групова дисперсія характеризує варіацію відносно групової середньої:
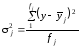 або
або
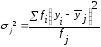 (2.74)
(2.74)
Оскільки в групи об’єднуються певною мірою схожі елементи сукупності, то варіація в групах, як правило, менша, ніж у цілому по сукупності. Якщо причинні комплекси, що формують варіацію в різних групах, неоднакові, то й групові дисперсії різняться між собою.
Узагальнюючою мірою внутрішньогрупової варіації є середня з групових дисперсій:
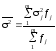 . (2.75)
. (2.75)
Різними
є й групові середні
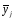 .
Мірою варіації їх навколо загальної
середньої є міжгрупова дисперсія
.
Мірою варіації їх навколо загальної
середньої є міжгрупова дисперсія
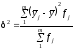 (2.76)
(2.76)
Взаємозв’язок дисперсій називається правилом (теоремою) розкладання дисперсії ( варіації):
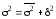 (2.77)
(2.77)
де
 — загальна дисперсія ознаки y;
— загальна дисперсія ознаки y;
 -
факторна дисперсія;
-
факторна дисперсія;
σ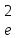 - залишкова дисперсія
- залишкова дисперсія
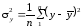 (2.78)
(2.78)
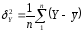 (2.79)
(2.79)
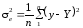 (2.81)
(2.81)
де Y, у - відповідно теоретичні та фактичні значення результативної ознаки.
Враховуючи,
що аналіз показників буде проводитися
за вибірковими даними, визначають
поняття довірчих меж показника, у тому
числі наводять відповідні формули. Так
межі довірчого інтервалу для середньої
визначаються на основі точкової оцінки
та граничної помилки вибірки
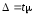 . Наприклад, для факторного показника
визначення довірчих меж ввідбувається
наступним чином:
. Наприклад, для факторного показника
визначення довірчих меж ввідбувається
наступним чином:
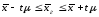 ;
(2.82)
;
(2.82)
де — стандартна (середня) помилка вибірки (необхідно надати її поняття);
t — квантиль розподілу ймовірностей (коефіцієнт довіри, що відповідає ймовірності ).
Величину стандартної помилки можна визначити за формулою для відбору:
повторного
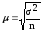 (2.83)
(2.83)
безповторного

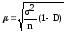 (2.84)
(2.84)
де n - обсяг вибірки,
D – частка вибіркової сукупності в генеральній
Таким чином, середня може розраховуватися різними формулами в залежності від виду економічного показника та типу вихідних даних. Для найбільшого наближення до реальних умов доцільно розрахувати стандартну помилку та визначити довірчий інтервал.
2.3 Методологія побудови та аналізу моделі парної регресії
Оскільки статистичні явища пов'язані між собою та обумовлюють одне, то необхідні спеціальні статистичні методи аналізу, які дозволяють вивчити форму, близькість та інші параметри статистичних взаємозв'язків. Одним з таких методів є кореляційний аналіз. На відміну від функціональних залежностей, при яких зміна будь-якої ознаки – функції – повністю та однозначно визначається зміною іншої ознаки-аргументу, при кореляційних формах зв'язку змінам одного або декількох факторів відповідає зміна середнього значення результативної ознаки. При цьому фактори, що розглядаються визначають результативну ознаку повністю.
За даними курсової роботи на рівень продуктивності праці впливають не тільки показники фондомісткості, стажу та інші, але й багато інших: технічний рівень виробництва, характер організації праці і т.д. У тому випадку, якщо досліджується зв'язок між одним фактором та однією ознакою, зв'язок має назву однофакторного та кореляція є парною. Якщо досліджується зв'язок між декількома факторами та однією ознакою, зв'язок має назву багатофакторного та кореляція є множинною.
На першому етапі дослідження взаємозв'язків між факторами необхідно з множини факторів, які сформовані шляхом інтуїтивних міркувань, відібрати ті, які дійсно вагомі з точки зору їхнього впливу на показник. Рішення завдань такого виду здійснюється за допомогою дисперсійного аналізу – однофакторного, якщо перевіряється істотність впливу того чи іншого фактора, або багатофакторного у випадку вивчення впливу на нього комбінації факторів.
Для вивчення зв'язку між явищами та їх ознакам будують кореляційну таблицю та аналітичне угрупування.
Кореляційна таблиця – це спеціальна комбінаційна таблиця, в якій наведено групування за двома пов'язаними ознаками: факторною та результативною. Концентрація частот біля діагоналей матриці свідчить про наявність кореляційного зв'язку між ознаками.
Аналітичне угрупування дозволяє вивчити взаємозв'язок факторної та результативної ознаки. Основні етапи проведення такого угрупування:
1. Обґрунтування факторної та результативної ознаки.
2. Підрахунок кількості одиниць в кожній з груп, що утворені.
3. Визначення обсягу ознак, що варіюють, в границях створених груп.
4. Розрахунок середніх значень результативної ознаки.
Результати групування оформлюються у таблиці (див. табл. 2.3).
Кількість груп можна визначити за формулою Стреджесса, методом «сігм» або прийняти самостійно.
Таблиця 2.3- Схема аналітичного угрупування
|
Межі угрупування по факторній ознаці, хj |
Кількість одиниць сукупності, fi |
Середнє значення результативної ознаки у групі j, уj |
|
|
f1 |
у1 |
|
|
f2 |
у2 |
|
|
:: |
:: |
|
Разом |
|
х |
Відомо, що якщо сукупність розбито на групи за певною ознакою х, то для будь-якої іншої ознаки у можна обчислити середню як у цілому по сукупності, так і в кожній групі. Центром розподілу сукупності в цілому є загальна середня
 або
або
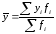 або
або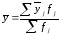 (2.85а)
(2.85а)
центром розподілу в j-й групі — групова середня
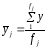 або
або
 (2.85б)
(2.85б)
де fi – частота і-го елементу сукупності,
nj = fj - обсяг j-ї групи,
n - обсяг сукупності
Для перевірки істотності зв'язку можна використовувати характеристику F-критерій (критерій Фішера), який визначається за формулою:
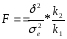 ,
(2.86а)
,
(2.86а)
де
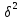 ,
, -
відповідно факторна (міжгрупова) та
залишкова дисперсія
-
відповідно факторна (міжгрупова) та
залишкова дисперсія
k1, k2 - число ступенів свободи відповідно факторної та залишкової дисперсії
![]() = m - 1;
= m - 1;
![]() =
n
– m (2.86б)
=
n
– m (2.86б)
де n, m - відповідно число одиниць сукупності та кількість груп.
 (2.87)
(2.87)
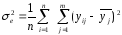 (2.88)
(2.88)
Тобто
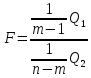 ,
(2.89а)
,
(2.89а)
де
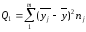 (2.89б)
(2.89б)
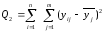 (2.89в)
(2.89в)
де уij – значення показника у, якій відповідає і-му елементу в j–й групі
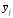 - середнє
значення показника у
в j–й
групі
- середнє
значення показника у
в j–й
групі
Надалі одержане розрахункове значення F порівнюється за табличним (критичним), для визначеного рівня істотності (звичайно 0,05 або 0,01) та ступенів свободи k1 та k2 .
Якщо Fрозр ≤ F табл, то вплив відповідного фактора визнається неістотним. Якщо, навпаки, Fрозр ≥ Fтабл – вплив істотний. Сформований у результаті процедури, що описана, набір істотних факторів використовується на наступних етапах дослідження: при побудові відповідних парних моделей регресії або рівняння множинної регресії.
Надалі
проведемо дослідження зв'язку між одним
фактором та однією ознакою, тобто аналіз
моделі парної регресії. Рівняння регресії
будемо досліджувати у вигляді Y=|![]() (де Y
— розрахунковий (теоретичний) рівень
результативної ознаки).
(де Y
— розрахунковий (теоретичний) рівень
результативної ознаки).
Розрахунок коефіцієнтів рівняння можна здійснити за формулами
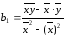 (2.9а)
(2.9а)

Необхідно побудувати кореляційне поле за емпіричними (вихідними) даними та «наложити» на нього лінію регресію, що побудована за визначенним рівнянням регресії, що дозволяє зробити попередні висновки про відповідність рівняння вихідним даним.
Вплив та напрямок однофакторного зв'язку характеризує лінійний коефіцієнт кореляції, який можна визначити за формулою
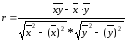 (2.9б)
(2.9б)
Зауважимо, що за формулою лінійного коефіцієнту розраховуються також парні коефіцієнти кореляції, які характеризують тісноту зв'язку між парами змінних, що розглядаються (без урахування їх взаємодії з іншими змінними).
Показником тісноти зв'язку між результативною та факторною ознакою є коефіцієнт детермінації (множинної кореляції)
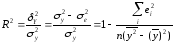 (2.9в)
(2.9в)
де
 — загальна дисперсія ознакиy;
— загальна дисперсія ознакиy;
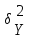 -
факторна дисперсія;
-
факторна дисперсія;
σ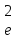 - залишкова дисперсія
- залишкова дисперсія
 (2.91а)
(2.91а)
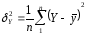 (2.91б)
(2.91б)
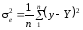 (2.91в)
(2.91в)
де Y, у|в| - відповідно розрахункові та фактичні значення результативної ознаки.
Тобто
 (2.91г)
(2.91г)
Якщо
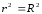 ,
це свідчить про лінійний зв'зок міжх
та у.
,
це свідчить про лінійний зв'зок міжх
та у.
Для встановлення адекватності моделі можна також використовувати F-критерій Фішера
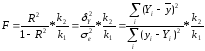 (2.92а)
(2.92а)
Тобто у випадку парної кореляції для лінійної моделі розрахункове значення F можна знайти за формулою
 (2.92б)
(2.92б)
Як і в методі аналітичних групувань, надалі одержане розрахункове значення F порівнюється за табличним (критичним) для визначеного рівня істотності (звичайно 0,05 або 0,01), тобто з Fα(1, n-2). Якщо Fрозр ≤ F табл, то вплив відповідного фактора визнається неістотним. Якщо, навпаки, Fрозр ≥ Fтабл – вплив істотний.
Необхідно також здійснювати оцінку статистичної значущості коефіцієнтів b0 та b1. Така оцінка здійснюється за допомогою t-критерію Ст'юдента. При цьому визначають розрахункові (фактичні) значення:
- для параметру b1
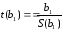 (2.93а)
(2.93а)
- для параметру b0
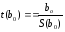 (2.93б)
(2.93б)
де S(b) – середньоквадратичне відхилення відповідного параметру
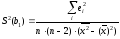 (2.93в)
(2.93в)
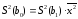 (2.93г)
(2.93г)
де S2(b) – дисперсія відповідного параметру
Розрахункові значення t-критерію Ст'юдента порівнюють з табличними, які обираються в залежності від рівня істотності та числа ступенів свободи
n -m -1 (де n – обсяг вибірки, m - кількість факторних ознак, що включено до моделі, тобто для однофакторної моделі число ступенів свободи дорівнює n-2). Критичні значення можна визначити за додатком 3 (наприклад, для одностороньої критичної області t0,05;14=1,76). Параметр визнається істотним, якщо розрахункове значення більше табличного.
За відповідними розрахунками можливо також одержати прогноз довірчого інтервалу для значення yn+1 та для його математичного очікування Myn+1.
Для значення yn+1 границі довірчих меж визначаються за формулою
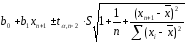 (2.94а)
(2.94а)
Для значення Myn+1 границі довірчих меж визначаються за формулою
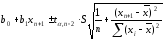 ,
(2.94б)
,
(2.94б)
де S2- незсунена оцінка для залишкової вибіркової дисперсії
 ,
(2.94в)
,
(2.94в)
2.4. Методологія множинного регресійного аналізу.
Економічні явища залежать від великої кількості факторів. Тому на практиці часто використовують рівняння множинної|факторів| регресії, коли на величину результативної ознаки впливають два і більш фактори.
Одна з умов кореляційного аналізу - однорідність досліджуваної інформації. Критерієм однорідності інформації служать коефіцієнти варіації, які розраховуються по кожному факторному й результативному показнику. Коефіцієнт варіації показує відносну міру відхилення окремих значень від середньоарифметичної.
Після|потім| відбору факторів і оцінки початкової|вихідної| інформації важливим|поважним| завданням|задачею| є|з'являється| моделювання зв'язку між факторним|факторами| і результативним показником. На практиці найчастіше використовують багатофакторні лінійні моделі |факторів| і моделі, які приводяться|наводять| до лінійного вигляду|виду| відповідними перетвореннями, тобто|цебто|
![]() (2.95а)
(2.95а)
Рішення задачі багатофакторного кореляційного аналізу передбачає визначення парних коефіцієнтів кореляції, які характеризують тісноту зв'язку між парами змінних, що розглядаються (без врахування їхньої взаємодії з іншими змінними). Парні коєфіцієнти кореляції можна розрахувати за формулою лінійного коефіцієнту (див. формулу 2.16).
Показником тісноти зв'язку між результативною та факторними ознаками є коефіцієнт множинної кореляції. У випадку лінійного двохфакторного зв'язку він може бути розрахован за формулою
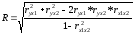 (2.95б)
(2.95б)
де r – лінійні (парні) коефіцієнти кореляції.
Значення цього коефіцієнту змінюється від 0 до 1. Коефіцієнт R2 має назву множинного коефіцієнту детермінації та показує, яка частка варіації результативної ознаки обумовлена впливом факторів, що враховано.
Наступним етапом кореляційно регресійного аналізу є побудова рівняння множинної регресії та визначення невідомих параметрів b0, b1 ,b2 ,….,bm обраноїх функції. Наприклад, рівняння двохфакторної лінійної регресії має вигляд
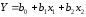 (2.96а)
(2.96а)
де Y - розрахункові значення результативної ознаки,
хі – значення факторних ознак,
b0, b1 ,b2 – параметри рівняння регресії
Для
визначення параметрів
![]() ,
,![]() ...
необхідно скласти і вирішити систему
нормальних рівнянь.При
двох факторах система
рівнянь набуває вигляду
...
необхідно скласти і вирішити систему
нормальних рівнянь.При
двох факторах система
рівнянь набуває вигляду
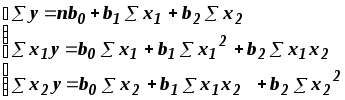 (2.96б)
(2.96б)
Рівняння лінійної множинної регресії можна також одержати, використовуючи програму «Microsoft Excel – Статистические функции – ЛИНЕЙН». Функція ЛИНЕЙН повертає масив {bm; bm-1; ... ; b1;b}, де m - кількість факторних ознак, що включено до моделі Синтаксис функції ЛИНЕЙН (відомі_значення_y;відомі_значення_x;конст;статистика)
Відомі_значення_y - це безліч значень y, що уже відомі для співвідношення y = b1x1 + b2x2 + ... + b
■ Якщо масив відомі_значення y має один стовпець, то кожний стовпець масиву відомі значення x інтерпретується як окрема змінна.
■ Якщо масив відомі значення y має один рядок, то кожний рядок масиву відомі значення x інтерпретується як окрема змінна.
Відомі значення x - це необов'язкова множина значень x, що уже відомі для співвідношення y = b1x1 + b2x2 + ... + b
■ Масив відомі значення x може містити одне або декілька множин змінних. Якщо використовується тільки одна змінна, то відомі значення y і відомі значення x можуть бути масивами будь-якої форми за умови, що вони мають однакову розмірність. Якщо використовується більш однієї змінної, то відомі значення y повинні бути вектором (тобто інтервалом висотою в один рядок або шириною в один стовпець).
■ Якщо відомі значення x опущені, то передбачається, що це масив {1;2;3;... } такого ж розміру як і відомі значення y.
Конст - це логічне значення, що вказує, чи потрібно, щоб константа b дорівнювала 0.
■ Якщо конст має значення ИСТИНА або опущена, то b обчислюється звичайним способом.
■ Якщо конст має значення ЛОЖЬ, то b покладається рівним 0 і значення bі підбираються так, щоб виконувалося співвідношення y = bx.
Статистика - це логічне значення, що вказує, чи потрібно повернути додаткову статистику по регресії.
■ Якщо статистика має значення ЛОЖЬ або опущена, то функція ЛИНЕЙН повертає тільки коефіцієнти bі і постійну b.
У цьому випадку регресійна статистика повертається за формою таблиці 2.4
Таблиця 2.4 – Регресійна статистика
|
bm |
bm-1 |
…. |
b2 |
b1 |
b |
Якщо статистика має значення ИСТИНА, то функція ЛИНЕЙН повертає додаткову регресійну статистику (див. табл. 2.5)
Таблиця 2.5 – Додаткова регресійна статистика
|
bm |
bm-1 |
…. |
b2 |
b1 |
b |
|
|
|
…. |
|
|
|
|
R2 |
|
|
|
|
|
|
F-критерій |
df (ступені свободи) |
|
|
|
|
|
|
|
|
|
|
|
Наступним етапом є розрахунок та перевірка статистичної значущості коефіцієнту детермінації, що відповідає визначеному теоретичному рівнянню, та значущості коефіцієнтів регресії.
Коефіцієнт детермінації, який надає оцінку загальної якості моделі, розраховується за формулою
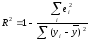 (2.97а)
(2.97а)
де
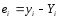
Перевірку статистичної істотності коефіцієнту детермінації можна здійснити за допомогою критерію Фішера, розрахункове значення якого визначається за формулою
 (2.98)
(2.98)
де n – обсяг вибірки,
m - кількість факторних ознак, що включено до моделі (кількість змінних у рівнянні)
Одержане розрахункове значення F порівнюється з табличним для визначеного рівня істотності , тобто з Fα (m; n -m -1). Якщо Fрозр ≥ Fтабл – коефіцієнт детермінації статистично значущ.
Оцінка істотності коефіцієнтів регресії здійснюється за допомогою t-критерію Ст'юдента. При цьому визначають розрахункові (фактичні) значення
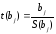 (2.99)
(2.99)
де
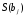 -
оцінка стандартної помилки коефіцієнту
-
оцінка стандартної помилки коефіцієнту
Розрахункові значення t-критерію Ст'юдента порівнюють з табличними, які обираються в залежності від рівня істотності та числа ступенів свободи
n-m-1. Параметр визначається істотним, якщо розрахункове значення перевищує табличне.
Висновки по розділу 2:
Для проведення статистичного дослідження необхідно згрупувати однорідну вихідну інформацію. При цьому ширину інтервалу визначають за формулою Стреджеса. Ряд розподілу за величиною груповочної ознаки можливо представити графічно у вигляді полігону або гістограми.
Розрахунок середньої може відбуватися за згрупованими або незгрупованими даними. У кожному випадку застосовують відповідні розрахункові формули. Для характеристики статистичного розподілу недостатньо охарактеризувати лише центр угрупування (середню величину), але необхідно знати також ступінь варіації елементів сукупності, який може бути розрахований за відповідними формулами.
Одним з методів оцінки взаємозв’язку між факторами є кореляційний аналіз. При цьому фактори, що розглядаються визначають результативну ознаку повністю. Тіснота зв’язку може бути розрахована за допомогою коефіцієнта множинної кореляції.

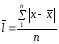
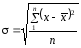

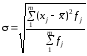
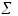 fi
fi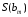
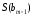
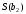
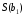
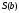
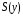 -
стандартна помилка для оцінки у
-
стандартна помилка для оцінки у