
- •1. История возникновения и развития метрологии.
- •2. Состояние и особенности применения измерительной техники в горной промышленности.
- •3. Направления и перспективы развития измерительной техники в горной промышленности.
- •4. Основные понятия и определения метрологии.
- •5. Измерительные устройства. Классификация измерительных устройств.
- •6. Измерительный преобразователь. Классификация измерительных преобразователей.
- •7. Нормативно-техническая, организационная и правовая основы метрологического обеспечения.
- •8. Понятие измерения. Классификация измерений.
- •9. Метод измерений. Классификация методов измерения.
- •10. Эталон. Классификация эталонов.
- •11. Эталон. Поверочные схемы.
- •12. Погрешность, классификация погрешностей.
- •13. Абсолютная, относительная и приведенная погрешности.
- •14. Методическая, инструментальная, систематическая и случайная погрешности.
- •15. Основная и дополнительная, статическая и динамическая погрешности.
- •16.Аддитивная и мультипликативная погрешность.
- •17.Погрешность квантования.
- •18.Понятие класса точности. Нормирование точности средств измерения.
- •19. Условные обозначения, принятые в измерительной технике.
- •6. Условия размещения прибора при измерениях:
- •7. Величина напряжения, которым испытана изоляция прибора:
- •20. Порядок поверки измерительных приборов. Требования к образцовому прибору.
- •21. Структура аналогового электромеханического прибора.
- •22. Магнитоэлектрическая измерительная система.
- •23. Электромагнитная измерительная система.
- •24 Электродинамическая измерительная система.
- •25. Ферродинамические измерительные системы
- •26. Электростатическая измерительная система.
- •27.Индукционная измерительная система.
- •28.Порядок обработки прямых и косвенных измерений.
- •29.Метрологические характеристики средств измерения в статике.
- •30.Метрологические характеристики средств измерения в динамике.
- •31. Структурная схема средства измерения. Классификация методов преобразования информации. Метод прямого преобразования.
- •32. Методы уравновешивающего и комбинированного преобразования.
- •33. Физическая величина. Единица физической величины. Международная система единиц.
- •34. Числовые параметры периодических сигналов.
- •35. Средства измерения силы тока. Схемы включения амперметров. Шунты.
- •36.Измерительные трансформаторы тока. Конструкция, векторная диаграмма, погрешности.
- •37 Средства измерения напряжения и особенности аналоговых вольтметров.
- •38. Методы и средства расширения пределов измерения вольтметров.
- •39.Методическая погрешность при измерении силы тока и напряжения.
- •40.Измерительные трансформаторы напряжения. Конструкция, векторная диаграмма, погрешности.
- •41.Цифровые вольтметры постоянного напряжения.
- •42.Вольтметр с времяимпульсным преобразованием.
- •Измерение сопротивления. Омметры.
- •Измерение сопротивления при помощи мостовых схем.
- •Измерение сопротивления методом вольтметра-амперметра.
- •47. Заземление. Измерение сопротивления заземления.
- •48. Методы и средства измерения мощности.
- •49. Измерение активной и реактивной мощности в трехфазных цепях.
- •50.Измерение мощности методом вольтметра-амперметра.
16.Аддитивная и мультипликативная погрешность.
Погрешности средств измерений - отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений). Погрешность результата измерения - отклонение результата измерения от действительного (истинного) значения измеряемой величины , определяемая по формуле - погрешность измерения.
Аддитивная погрешность– погрешность измерения которая при всех значениях входной измеряемой величины Х значения выходной величины Y изменяются на одну и ту же величину большую или меньшую от номинального значения.
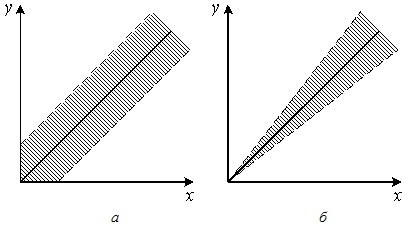
Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью .
Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).
Класс точности измерений :
-
для аддитивной погрешности:
![]() где
Х - верхний предел шкалы, ∆0 -
абсолютная аддитивная погрешность.
где
Х - верхний предел шкалы, ∆0 -
абсолютная аддитивная погрешность.
Мультипликативной
погрешностью называется
погрешность, линейно возрастающая или
убывающая с ростом измеряемой величины.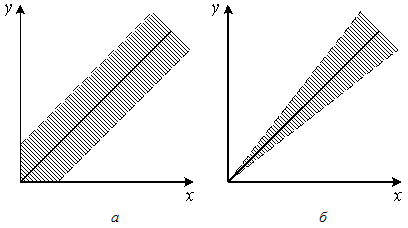
Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной
Класс точности измерений :
-
для мультипликативной погрешности:
![]()
![]() -
это условие определяет порог
чувствительности прибора (измерений).
-
это условие определяет порог
чувствительности прибора (измерений).
17.Погрешность квантования.
Погрешности
средств измерений -
отклонения метрологических свойств
или параметров средств измерений от
номинальных, влияющие на погрешности
результатов измерений (создающие так
называемые инструментальные ошибки
измерений).
Погрешность результата
измерения - отклонение результата
измерения от действительного (истинного)
значения измеряемой величины , определяемая
по формуле - погрешность измерения.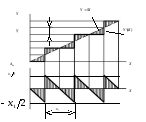
Разным
значениям непрерывной измеряемой
величины
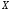 соответствуют дискретные значения
выходной величины
соответствуют дискретные значения
выходной величины .
Показания прибора дискретны с шагом
квантования
.
Показания прибора дискретны с шагом
квантования ,
где
,
где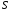 — чувствительность линейной функции
— чувствительность линейной функции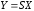 ,
которая имела бы место при
,
которая имела бы место при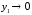 .
.
Значение
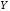 ,
соответствующее зависимости
,
соответствующее зависимости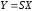 заменяется дискретным значением
заменяется дискретным значением ,
равнымближайшему
уровню квантования. Несовпадение
,
равнымближайшему
уровню квантования. Несовпадение
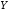 и
и будет определять погрешность квантования.
Значения погрешности квантования
будет определять погрешность квантования.
Значения погрешности квантования лежат в пределе от
лежат в пределе от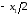 до
до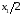 .
При этом все значения
.
При этом все значения равновероятны и математическое ожидание
такой погрешности равно 0. Из этого
следует, что в этом случае погрешность
квантования есть чисто случайная
погрешность с равномерным распределением.
равновероятны и математическое ожидание
такой погрешности равно 0. Из этого
следует, что в этом случае погрешность
квантования есть чисто случайная
погрешность с равномерным распределением.
18.Понятие класса точности. Нормирование точности средств измерения.
Класс точности (КТ)— это обобщенная характеристика средства измерений, выражаемая пределами его допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.
Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых при помощи этих средств.
Для того чтобы заранее оценить погрешность, которую внесет данное средство измерений в результат, пользуются нормированными значениями погрешности. Под ними понимают предельные для данного типа средства измерений погрешности.
Погрешность данного измерительного прибора не должна превосходить нормированного значения.
Если обозначаемое на шкале значение класса точности обведено кружком, например 1,5, это означает, что погрешность чувствительности γs=1,5%. Так нормируют погрешности масштабных преобразователей (делителей напряжения, шунтов, измерительных трансформаторов тока и напряжения и т. п.).
Если на шкале измерительного прибора цифра класса точности не подчеркнута, например 0,5, это означает, что прибор нормируется приведенной погрешностью нуля γ о=0,5 %.
Однако будет грубейшей ошибкой полагать, что амперметр класса точности 0,5 обеспечивает во всем диапазоне измерений погрешность результатов измерений ±0,5 %.
На измерительных приборах с резко неравномерной шкалой (например на омметрах) класс точности указывают в долях от длины шкалы и обозначают как 1,5 с обозначением ниже цифр знака "угол".
Если обозначение класса точности на шкале измерительного прибора дано в виде дроби (например 0,02/0,01), это указывает на то, что приведенная погрешность в конце диапазона измерений γк = ±0,02 %, а в нуле диапазона γн = ±0,01 %. К таким измерительным приборам относятся высокоточные цифровые вольтметры, потенциометры постоянного тока и другие высокоточные приборы. В этом случае
δ(х) = γк + γн (Хк/Х - 1),
где Хк - верхний предел измерений (конечное значение шкалы прибора), Х — измеряемое значение.
