
кЛТ. 10.20. к‡Т˜ВЪМ‡fl ТıВП‡ НУПФУМУ‚УН„ Ë ‰ (‚ÚÓ ÓÈ ÒÎÛ˜‡È)
кЛТ. 10.21. к‡Т˜ВЪМ‡fl ТıВП‡ НУПФУМУ‚УН Â Ë Ê
2
I2 – ПУПВМЪ ЛМВ ˆЛЛ ФУФВ В˜МУ„У ТВ˜ВМЛfl ФОВ˜‡ éÄ; I1 – ПУПВМЪ ЛМВ ˆЛЛ ФУФВ В˜МУ„У ТВ˜ВМЛfl ЪЫ ·У·Ы ‡.
éÒڇθÌ˚ ӷÓÁ̇˜ÂÌËfl ÒÏ. ËÁ ËÒ. 10.18.
мТОУ‚ЛВ ‚УБПУКМУ„У Ф УФЫТН‡ (Ф УıУК‰ВМЛfl) НУПФУМУ‚НЛ ˜В ВБ НУМ‰ЫНЪУ
|
|
|
d 1 |
+ d2 |
|
|
|
|
|
|
||||||
|
2 σ Dc − |
|
|
|
EI2 |
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
QÍ > |
|
|
|
|
|
|
|
|
|
|
1 |
+ |
|
|
, |
|
|
|
|
|
L3 |
|
|
|
|
|
L |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
„‰Â QÍ |
– ‚ВТ НУПФУМУ‚НЛ; – НУ˝ЩЩЛˆЛВМЪ Ъ ВМЛfl НУПФУ- |
|||||||||||||||
ÌÓ‚ÍË Ó ÍÓ̉ÛÍÚÓ . |
|
|
|
|
|
|
||||||||||
ìÒÎÓ‚Ë Á‡ÔÛÒ͇ ÚÛ ·ËÌ˚ |
|
|
||||||||||||||
|
|
|
d1 |
+ d2 |
|
|
|
|
|
|
||||||
|
|
6 Dc − |
|
|
EI2 |
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
D‰ |
|
|
|
|
|
|||||
MÚ > |
|
|
|
|
|
|
, |
|
|
|
||||||
|
L 2L1 |
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
„‰Â åÚ – ЪУ ПУБМУИ ПУПВМЪ ЪЫ ·ЛМ˚.
СОfl НУПФУМУ‚УН “‚ ” Ô Ë I1 >> I2 ‡Т˜ВЪМ˚В ЩУ ПЫО˚ УТ- Ъ‡˛ЪТfl ТФ ‡‚В‰ОЛ‚˚ПЛ Т ЫФ У˘ВМЛВП
|
|
d1 |
+ d2 |
|
|
|
|||||
|
3 Dc − |
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
L = |
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
||||
|
|
d |
|
D |
2 |
|
1 |
|
|
||
|
α Ô − Dc − |
1 |
− |
|
|
|
|
|
|||
|
2 |
2 |
|
L |
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
СОfl НУПФУМУ‚УН “„” Ë “‰” ‡ТТПУЪ ЛП ‰‚‡ ТОЫ˜‡fl ‡ТФУОУКВМЛfl.
ê‡Ò˜ÂÚ̇fl ÒıÂχ ‰Îfl Ô ‚Ó„Ó ÒÎÛ˜‡fl Ô Ë‚Â‰Â̇ ̇ ËÒ. 10.19.
è ˂‰ÂÌÌ˚ ÙÓ ÏÛÎ˚ ·Û‰ÛÚ ÒÔ ‡‚‰ÎË‚˚ ‰Îfl
|
|
|
D‰ |
|
d |
|
|
|
Dc − |
|
− |
1 |
|
α1 |
< |
2 |
2 |
|
||
|
L |
|
|
|
||
|
|
|
|
|
|
Ë ÛÒÎÓ‚ËÈ ÛÔ Û„Ëı ‰ÂÙÓ Ï‡ˆËÈ
|
|
d2 + d3 |
|
|
|
6 Dc − |
|
Ed3 |
|
2 |
|
|||
|
|
|
|
|
σ = |
|
|
|
< [σÚ]. |
|
2L2 |
|
||
|
|
|
|
á‰ÂÒ¸
591
L = |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
||
|
|
|
|
|
D‰ |
|
|
|
d |
2 |
|
|
|
|
|
1 |
|
|
|
d L |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
2 α 2 |
− Dc − |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
2 |
|
L |
|
+ |
L |
|
|
L |
+ |
L |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
d2 + d3 |
|
|
|
|
|
|
|
|
|
d2 + d3 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
× 3 |
Dc − |
|
|
|
|
|
|
+ 9 Dc − |
|
|
|
|
|
|
|
+ |
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Dc − |
D‰ |
− |
d2 |
|
|
|
α L |
|
|
|
|
|
|
|
|
d2 |
+ d3 |
|
I1 |
||||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
+8 |
α2 − |
|
|
|
|
+ |
|
|
|
1 1 |
|
|
× |
Dc − |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
L1+ L2 |
|
|
|
|
|
L1+ L2 |
|
|
|
|
|
|
|
|
|
2 |
|
I3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/2
(L1 + L2)] ,
„‰Â I1 – ПВМ¸¯ЛИ ЛБ ПУПВМЪУ‚ ЛМВ ˆЛЛ ФУФВ В˜МУ„У ТВ˜В- МЛfl ФВ ‚У„У Л ‚ЪУ У„У ФОВ˜‡; I3 – ПУПВМЪ ЛМВ ˆЛЛ ФУФВ В˜- МУ„У ТВ˜ВМЛfl НО˛˜‡ éÄ.
мТОУ‚ЛВ Ф УФЫТН‡ (Ф УıУК‰ВМЛfl) ˜В ВБ НУМ‰ЫНЪУ
|
|
|
|
|
|
|
|
|
|
|
d2 |
+ d3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 6 Dc − |
|
|
|
|
|
|
|
|
EI3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
L |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
QÍ > |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
L3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L + L2 |
|
|
|||||||||
ЗУБПУКМУТЪ¸ Б‡ФЫТН‡ ЪЫ ·ЛМ˚ |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d2 |
+ d3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
6 Dc |
− |
|
|
|
|
|
|
|
|
|
EI3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
D |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
‰ |
|
|
|
|
|
|
|||||||||||||
MÚ > µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
L3(L1 + L2) |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
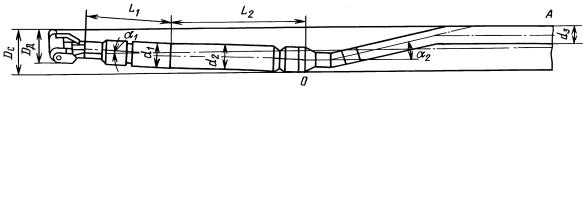
ê‡Ò˜ÂÚ̇fl ÒıÂχ |
|
|
НУПФУМУ‚УН |
“” |
Ë “‰” (‚ÚÓ ÓÈ ÒÎÛ˜‡È) |
|||||||||||||||||||||||||||||||||
Ô Ë‚Â‰Â̇ ̇ ËÒ 10.20. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
è Ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
D‰ |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Dc |
− |
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
α1 > |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ÛÒÎÓ‚Ë ÛÔ Û„Ëı ‰ÂÙÓ Ï‡ˆËÈ |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
d2 + d3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
6 Dc |
− |
|
|
|
|
|
|
|
|
|
|
Ed3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
σ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< [σÚ], |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2L2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
„‰Â |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2 |
+ d3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
L= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
Dc − |
|
|
|
+ |
||||
|
|
|
|
|
|
|
d |
D |
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2 α |
1 |
− |
|
D |
c |
− |
1 |
− |
|
|
|
|
+ |
α |
2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
592

кЛТ. 10.22. дУПФУМУ‚Н‡ МЛБ‡ ·Ы ЛО¸МУИ НУОУММ˚ ‰Оfl ·Ы ВМЛfl Ы˜‡ТЪН‡ ТЪ‡·ЛОЛБ‡ˆЛЛ БВМЛЪМУ„У Ы„О‡:
1 – ‰УОУЪУ; 2 – ͇ÎË· ‡ÚÓ ; 3 – ÚÛ ·Ó·Û ; 4 – ˆÂÌÚ-‡ÚÓ
|
|
|
d |
2 |
+ d |
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
d |
D‰ 1 |
|
||||||||||
+ 9 |
Dc − |
|
|
|
|
|
|
|
+ 8 α1 − Dc − |
1 |
− |
|
|
|
+ α2 × |
|||||||||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 L1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 |
− d I |
|
|
1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
× Dc − |
|
|
|
1 |
|
|
2 |
L1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
I2 – М‡ЛПВМ¸¯ЛИ ЛБ ПУПВМЪУ‚ ЛМВ ˆЛЛ |
||||||||||||||||||||||||||||||||
ÔÓÔ ˜Ì˚ı Ò˜ÂÌËÈ ‚ÚÓ Ó„Ó ÔΘ‡ Ë |
ÔΘ‡ |
|||||||||||||||||||||||||||||||
éÄ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìÒÎÓ‚ËÂ |
Ф УФЫТН‡ |
|
|
|
(Ô ÓıÓʉÂÌËfl) |
˜Â ÂÁ |
||||||||||||||||||||||||||
ÍÓ̉ÛÍÚÓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
d2 |
+ d3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 6 Dc − |
|
|
|
|
|
|
EI2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
|
L |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
QÍ > |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
L3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 |
|
|
|
|
|
|
||||||
ìÒÎÓ‚Ë Á‡ÔÛÒ͇ ÚÛ ·ËÌ˚ |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
d2 |
+ d3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
6 Dc − |
|
|
|
|
|
|
EI2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
‰ |
|
|
|
|
|
|
|
|
|
||||||
MÚ > µ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
L2L1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
к‡Т˜ВЪМ‡fl ТıВП‡ НУПФУМУ‚УН “” Ë “Ê” Ô Ë‚Â‰Â̇ ̇ ËÒ. 10.21.
н‡Н Н‡Н М‡НО‡‰Н‡ ‡ТТ˜ЛЪ‡М‡ М‡ ‡·УЪЫ ‚ Н Л‚УП ТЪ‚УОВ, flТМУ, ˜ЪУ НУМВˆ ЪЫ ·У·Ы ‡ МВ ·Ы‰ВЪ Н‡Т‡Ъ¸Тfl МЛКМВИ ТЪВМНЛ НУМ‰ЫНЪУ ‡.
ìÒÎÓ‚Ë ÛÔ Û„Ëı ‰ÂÙÓ Ï‡ˆËÈ
σ = 2(α Ô − α1)Eα 3 < [σÚ].
2L
á‰ÂÒ¸
|
3 |
|
|
|
|
|
|
|
|
d |
|
|
d |
|
||||
L = |
|
|
|
|
L2(αÔ − α1) + Dc |
− |
|
3 |
|
− f + |
|
Ú |
; |
|||||
α Ô − α1 |
2 |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dÚ – ‰Ë‡ÏÂÚ ÚÛ ·Ó·Û ‡; |
|
|
|
|
|
|
|
|
||||||||||
|
|
Dc |
− |
d‰ |
− f − |
dÚ |
|
|
|
|
|
|
|
|
|
|||
α1 = |
2 |
2 |
. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
||
593
мТОУ‚ЛВ Ф УФЫТН‡ (Ф УıУК‰ВМЛfl) ˜В ВБ НУМ‰ЫНЪУ
|
|
2(α Ô − α1)EI3 |
L + L2 |
||||||||
QÍ = 2 |
|
|
|
|
|
1+ |
|
|
|
. |
|
|
|
L2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
L1 |
||||
ìÒÎÓ‚Ë Á‡ÔÛÒ͇ ÚÛ ·ËÌ˚ |
|||||||||||
MÚ > |
2(α |
Ô |
− α )EI |
3 |
(L+ L2) |
D‰ |
. |
|
|||
|
|
1 |
|
|
|||||||
|
|
|
L2L1 |
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||
з‡ ЛТ. 10.22 Ф Л‚В‰ВМ‡ НУПФУМУ‚Н‡ МЛБ‡ ·Ы ЛО¸МУИ НУОУММ˚, „‰В L – ЛТНУП‡fl УФЪЛП‡О¸М‡fl ‰ОЛМ‡ НУПФУМУ‚НЛ.
10.4.3. ЗхЕйк ЬЦлндап дйеийзйЗйд заЬзЦв уДлна Емкагъзйв дйгйззх Сгь лнДЕагабДсаа мЙгД зДикДЗгЦззйв лдЗДЬазх
лЪ‡·ЛОЛБ‡ˆЛfl Ы„О‡ Ф flПУОЛМВИМУ„У Ы˜‡ТЪН‡ М‡НОУММУ М‡Ф ‡‚ОВММУИ ТН‚‡КЛМ˚ fl‚ОflВЪТfl ‚‡КМВИ¯ЛП ˝Ъ‡- ФУП ВВ Ф У‚У‰НЛ, Ъ‡Н Н‡Н Ф flПУОЛМВИМ˚И Ы˜‡ТЪУН, Н‡Н Ф ‡-
|
|
|
|
|
í‡ · Πˈ ‡ |
10.6 |
||
|
|
|
|
|
|
|
||
|
|
ê‡ÒÒÚÓflÌË ÓÚ ÚÓ ˆ‡ ‰ÓÎÓÚ‡ ‰Ó |
||||||
дУПФУМУ‚Н‡ МЛБ‡ ·Ы ЛО¸МУИ |
лФУТУ· |
Ò ‰ËÌ˚ ˆÂÌÚ ‡ÚÓ ‡, Ï Ô Ë |
||||||
НУОУММ˚ |
·Û ÂÌËfl |
|
БВМЛЪМУП Ы„ОВ, „ ‡‰ЫТ |
|
||||
|
|
15 |
|
20 |
25 |
30 |
|
35 |
СУОУЪУ ‰Л‡ПВЪ УП 295,3 ПП, Н‡- |
êÓÚÓ - |
8,0 |
|
7,7 |
7,2 |
6,8 |
|
6,6 |
ÎË· ‡ÚÓ ‰Ë‡ÏÂÚ ÓÏ 295,3 ÏÏ, |
Ì˚È |
|
|
|
|
|
|
|
ìÅí ‰Ë‡ÏÂÚ ÓÏ 203 ÏÏ, ͇ÎË· ‡- |
|
|
|
|
|
|
|
|
ÚÓ ‰Ë‡ÏÂÚ ÓÏ 295,3 ÏÏ; ìÅí |
|
|
|
|
|
|
|
|
‰Ë‡ÏÂÚ ÓÏ 203 ÏÏ |
|
|
|
|
|
|
|
|
СУОУЪУ ‰Л‡ПВЪ УП 295,3 ПП; Н‡- |
êÓÚÓ - |
8,2 |
|
7,8 |
7,4 |
7,1 |
|
6,0 |
ÎË· ‡ÚÓ ‰Ë‡ÏÂÚ ÓÏ 295,3 ÏÏ; |
Ì˚È |
|
|
|
|
|
|
|
ìÅí ‰Ë‡ÏÂÚ ÓÏ 229 ÏÏ, ͇ÎË· ‡- |
|
|
|
|
|
|
|
|
ÚÓ ‰Ë‡ÏÂÚ ÓÏ 295,3 ÏÏ; ìÅí |
|
|
|
|
|
|
|
|
‰Ë‡ÏÂÚ ÓÏ 229 ÏÏ |
|
|
|
|
|
|
|
|
СУОУЪУ ‰Л‡ПВЪ УП 295,3 ПП; Н‡- |
íÛ ·ËÌ- |
7,7 |
|
7,2 |
6,8 |
6,5 |
|
6,0 |
ÎË· ‡ÚÓ ‰Ë‡ÏÂÚ ÓÏ 295,3 ÏÏ; |
Ì˚È |
|
|
|
|
|
|
|
ÚÛ ·Ó·Û 3íë 5Å-240 ËÎË 3íëò- |
|
|
|
|
|
|
|
|
240; ìÅí ‰Ë‡ÏÂÚ ÓÏ 203 ÏÏ. ç‡ |
|
|
|
|
|
|
|
|
ÍÓ ÔÛÒ ÚÛ ·Ó·Û ‡ ˆÂÌÚ ‡ÚÓ |
|
|
|
|
|
|
|
|
‰Ë‡ÏÂÚ ÓÏ 292 ÏÏ |
|
|
|
|
|
|
|
|
СУОУЪУ ‰Л‡ПВЪ УП 215,9 ПП; Н‡- |
êÓÚÓ - |
6,5 |
|
6,0 |
5,7 |
5,5 |
|
5,0 |
ÎË· ‡ÚÓ ‰Ë‡ÏÂÚ ÓÏ 215,9 ÏÏ, |
Ì˚È |
|
|
|
|
|
|
|
ìÅí ‰Ë‡ÏÂÚ ÓÏ 178 ÏÏ; ͇ÎË· ‡- |
|
|
|
|
|
|
|
|
ÚÓ ‰Ë‡ÏÂÚ ÓÏ 215,9 ÏÏ; ìÅí |
|
|
|
|
|
|
|
|
‰Ë‡ÏÂÚ ÓÏ 178 ÏÏ |
|
|
|
|
|
|
|
|
СУОУЪУ ‰Л‡ПВЪ УП 215,9 ПП; Н‡- |
íÛ ·ËÌ- |
5,0 |
|
4,5 |
4,3 |
4,0 |
|
3,0 |
ÎË· ‡ÚÓ ‰Ë‡ÏÂÚ ÓÏ 215,9 ÏÏ; |
Ì˚È |
|
|
|
|
|
|
|
ÚÛ ·Ó·Û 3íëò-185, ìÅí ‰Ë‡- |
|
|
|
|
|
|
|
|
ÏÂÚ ÓÏ 178 ÏÏ. ç‡ ÍÓ ÔÛÒ ÚÛ - |
|
|
|
|
|
|
|
|
·Ó·Û ‡ ˆÂÌÚ ‡ÚÓ ‰Ë‡ÏÂÚ ÓÏ |
|
|
|
|
|
|
|
|
215 ÏÏ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
594
‚ЛОУ, – М‡Л·УОВВ Ф УЪflКВММ˚И ˝ОВПВМЪ Ф УЩЛОfl, УФ В‰ВОfl˛- ˘ЛИ ЫТФВ¯МУВ ‰УТЪЛКВМЛВ Б‡·УВП ТН‚‡КЛМ˚ Б‡‰‡ММУИ ЪУ˜НЛ.
СОfl ‚˚ФУОМВМЛfl ЫН‡Б‡ММУИ Б‡‰‡˜Л МВУ·ıУ‰ЛПУ ТУ·О˛‰‡Ъ¸ ТОВ‰Ы˛˘ЛВ У·˘ЛВ ФУОУКВМЛfl.
1. дУПФУМУ‚Н‡ ‰УОКМ‡ ЛПВЪ¸ МВ ПВМВВ ‰‚Ыı ˆВМЪ Л Ы˛- ˘Лı ˝ОВПВМЪУ‚, ‰Л‡ПВЪ НУЪУ ˚ı ‡‚ВМ ‰Л‡ПВЪ Ы ‰УОУЪ‡ Ф ЛУЪУ МУП ·Ы ВМЛЛ, ‡ Ф Л ·Ы ВМЛЛ Б‡·УИМ˚П ‰‚Л„‡ЪВОВП ‰Л‡- ПВЪ ˆВМЪ ‡ЪУ ‡ ‰УОКВМ ·˚Ъ¸ М‡ 3 ПП ПВМ¸¯В МУПЛМ‡О¸МУ„У ‰Л‡ПВЪ ‡ ‰УОУЪ‡. иВ ‚˚И ˝ОВПВМЪ – Н‡ОЛ· ‡ЪУ Ф ЛТУВ‰ЛМflВЪТfl МВФУТ В‰ТЪ‚ВММУ Н ‰УОУЪЫ (·ВБ ФВ В‚У‰МЛН‡).
2.СОЛМ‡ НУПФУМУ‚НЛ ‰УОКМ‡ ·˚Ъ¸ УФЪЛП‡О¸МУИ. З Н‡˜ВТЪ- ‚В Н ЛЪВ Лfl, УФ В‰ВОfl˛˘В„У УФЪЛП‡О¸МЫ˛ ‰ОЛМЫ НУПФУМУ‚НЛ, Ф ЛМflЪУ ‡‚ВМТЪ‚У МЫО˛ ТЛО˚, Ф ЛОУКВММУИ Н ‰УОУЪЫ Л М‡- Ф ‡‚ОВММУИ ФВ ФВМ‰ЛНЫОfl МУ Н УТЛ ТЪ‚УО‡ ТН‚‡КЛМ˚.
3.йФЪЛП‡О¸М‡fl ‰ОЛМ‡ НУПФУМУ‚НЛ ‰УОКМ‡ У·ВТФВ˜Л‚‡Ъ¸ ВВ Ф УıУ‰ЛПУТЪ¸ М‡ Ы˜‡ТЪНВ ‚˚·У ‡ Ы„О‡ Т ЛМЪВМТЛ‚МУТЪ¸˛ ЛТ- Н Л‚ОВМЛfl, ТУУЪ‚ВЪТЪ‚Ы˛˘ВИ Ф УВНЪМУПЫ Ф УЩЛО˛.
СОfl ˝ЩЩВНЪЛ‚МУИ ‡·УЪ˚ НУПФУМУ‚НЛ ‚ Ф УˆВТТВ ·Ы ВМЛfl ТОВ‰ЫВЪ ФУ‰‰В КЛ‚‡Ъ¸ МУПЛМ‡О¸М˚В ‡БПВ ˚ Н‡ОЛ· ‡ЪУ У‚ Л ˆВМЪ ‡ЪУ ‡, ЫТЪ‡М‡‚ОЛ‚‡ВПУ„У М‡ Б‡·УИМУП ‰‚Л„‡ЪВОВ.
З Ъ‡·О. 10.6 Ф Л‚В‰ВМ˚ ВБЫО¸Ъ‡Ъ˚ ‡Т˜ВЪУ‚ УФЪЛП‡О¸МУИ ‰ОЛМ˚ НУПФУМУ‚УН ‰Оfl ТЪ‡·ЛОЛБ‡ˆЛЛ Ы„О‡ М‡НОУММУ М‡Ф ‡‚- ОВММ˚ı ТН‚‡КЛМ.
10.5. еЦнйСх а млнкйвлнЗД дйзнкйгь нкДЦднйкаа зДикДЗгЦззхп лдЗДЬаз
ЗВ ЪЛН‡О¸М‡fl (МВМ‡Ф ‡‚ОВММ‡fl) ТН‚‡КЛМ‡ ·Ы-ЛЪТfl Ф Л ФУТЪУflММУП Ы„ОВ М‡НОУМ‡, НУЪУ ˚И ФУ‰‰В КЛ‚‡ВЪТfl ‚ Б‡‰‡ММ˚ı Ф В‰ВО‡ı, ‚ ЪУ ‚ ВПfl Н‡Н Ф Л М‡Ф ‡‚ОВММУП ·Ы ВМЛЛ Ы„УО Л ‡БЛПЫЪ Ъ ‡ВНЪУ ЛЛ ТЪ‚УО‡ ‰УОКМ˚ ·˚Ъ¸ УФ-В‰ВОВММ˚ПЛ, Н‡Н, М‡Ф ЛПВ , ЛБУ· ‡КВМУ М‡ ЛТ. 10.23.
уЪУ·˚ ФУН‡Б‡Ъ¸ ЛБПВМВМЛfl НУМЩЛ„Ы ‡ˆЛЛ ТЪ‚УО‡, Ф У‚У- ‰flЪ В‰ЛМЛ˜М˚В ‚˚·У У˜М˚В ЛБПВ ВМЛfl. щЪЛ ЛБПВ ВМЛfl ˜‡ТЪУ
ПУКМУ ТУ‚ПВТЪЛЪ¸ Т МВФ У‰УОКЛЪВО¸М˚ПЛ ФВ В ˚‚‡ПЛ ‚ ‡- ·УЪВ ·Ы У‚У„У ТЪ‡МН‡, ‚ ЪВ˜ВМЛВ ‚ТФУПУ„‡ЪВО¸М˚ı УФВ ‡ˆЛИ, М‡Ф ЛПВ , МВФУТ В‰ТЪ‚ВММУ ФВ В‰ ФУ‰˙ВПУП ·Ы ЛО¸М˚ı Ъ Ы· ‰Оfl ТПВМ˚ ‰УОУЪ‡. ЕУОВВ Ф У„ ВТТЛ‚М˚В ТЛТЪВП˚, Ъ‡НЛВ Н‡Н НУМЪ УОЛ Ы˛˘ЛВ ЛМТЪ ЫПВМЪ˚ ЛОЛ ЛБПВ ЛЪВО¸М˚В ТЛТЪВП˚ ‚ Ф УˆВТТВ ·Ы ВМЛfl (еWD), ‚ НУМН ВЪМ˚В ПУПВМЪ˚ ‚ ВПВМЛ Ф В‰ТЪ‡‚Оfl˛Ъ ‰‡ММ˚В У М‡Ф ‡‚ОВМЛЛ ТЪ‚УО‡, НУЪУ ˚В ФУН‡- Б˚‚‡˛Ъ, ˜ЪУ Ф УЛТıУ‰ЛЪ М‡ Б‡·УВ ‚ Ф УˆВТТВ ·Ы ВМЛfl.
595
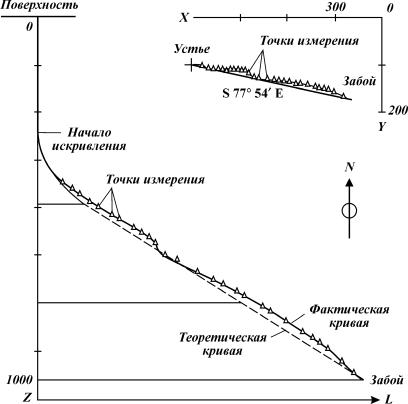
кЛТ. 10.23. к‡Т˜ВЪМ‡fl Л Щ‡НЪЛ˜ВТН‡fl Ъ ‡ТТ˚ ТЪ‚УО‡ М‡Ф ‡‚ОВММУИ ТН‚‡КЛМ˚
лВ ‚ЛТМ‡fl НУПФ‡МЛfl ФУ ВБЫО¸Ъ‡Ъ‡П ЛТТОВ‰У‚‡МЛfl ТН‚‡КЛ- М˚ „УЪУ‚ЛЪ НУПФОВНТМ˚И УЪ˜ВЪ У ТН‚‡КЛМВ, У·˚˜МУ Ъ‡НУИ, Н‡НУИ Ъ В·ЫВЪТfl ФВ В‰ ТФЫТНУП У·Т‡‰М˚ı НУОУММ ЛОЛ ФУТОВ ТФЫТН‡, ЛОЛ ФУТОВ Б‡Н‡М˜Л‚‡МЛfl ТН‚‡КЛМ˚. аМТЪ ЫПВМЪ‡О¸- М˚В ЛБПВ ВМЛfl Л ЛТТОВ‰У‚‡МЛfl Ф У‚У‰flЪ ‚ МВТНУО¸НЛı Б‡ФО‡-
МЛ У‚‡ММ˚ı ЛМЪВ ‚‡О‡ı. щЪЛ ЛТТОВ‰У‚‡МЛfl ‡М‡ОЛБЛ Ы˛Ъ У·˚˜МУ М‡ НУПФ¸˛ЪВ В ‚ ˆВОflı У·ВТФВ˜ВМЛfl ЪУ˜МУИ Ъ ‡ВНЪУ-ЛЛ ТН‚‡КЛМ˚.
н В·У‚‡МЛfl Н ЛТТОВ‰У‚‡МЛflП Л ЛМЪВ ‚‡О‡П ‚‡ ¸Л Ы˛Ъ ‚‡БОЛ˜М˚ı НУПФ‡МЛflı, ¯Ъ‡Ъ‡ı Л МВЩЪflМ˚ı Ф УП˚ТО‡ı. н‡Н, М‡ ФУ·В ВК¸В Б‡ОЛ‚‡ ‚ лтД М‡Ф ‡‚ОВММ˚В ТН‚‡КЛМ˚ ‰УОК- М˚ ЛТТОВ‰У‚‡Ъ¸Тfl ˜В ВБ Н‡К‰˚В 50–70 П Ф УıУ‰НЛ, ‡ М‡ УНВ- ‡МТНУП ФУ·В ВК¸В – ˜В ВБ 30–50 П. н‡П, „‰В ТН‚‡КЛМ˚
596
У˜ВМ¸ ·ОЛБНУ ‡ТФУОУКВМ˚, М‡Ф ЛПВ , Ф Л ·Ы ВМЛЛ Т ПУ - ТНЛı ФО‡ЪЩУ П, ЛМЪВ ‚‡О˚ Ф УıУ‰НЛ ПВК‰Ы ЛТТОВ‰У‚‡МЛflПЛ ПУ„ЫЪ ·˚Ъ¸ ЫПВМ¸¯ВМ˚ ‰У 30–10 П, ˜ЪУ·˚ МВ ФВ ВТВ˜¸Тfl Т ‰ Ы„ЛПЛ ТН‚‡КЛМ‡ПЛ. щЪЛ ТН‚‡КЛМ˚ ˜‡ТЪУ Ф У·Л‚‡˛ЪТfl ЫФ-‡‚ОflВП˚П ЛМТЪ ЫПВМЪУП.
З ˆВОУП ‰Оfl ТВ ‚ЛТМУ„У У·ТОЫКЛ‚‡МЛfl М‡Ф ‡‚ОВММУ„У ·Ы-ВМЛfl ЛТФУО¸БЫ˛Ъ ‡БОЛ˜М˚В ТЛТЪВП˚: УЪ ·УОВВ ТЪ‡ ˚ı Ф У- ТЪВИ¯Лı ЛМТЪ ЫПВМЪУ‚, ‰У МУ‚ВИ¯Лı ФУТЪУflММУ ‰ВИТЪ‚Ы˛- ˘Лı Б‡·УИМ˚ı В„ЛТЪ ‡ЪУ У‚. з‡ЛОЫ˜¯Ы˛ ТЛТЪВПЫ ‰Оfl Н‡К- ‰У„У НУМН ВЪМУ„У ТОЫ˜‡fl УФ В‰ВОflВЪ Б‡Н‡Б˜ЛН Т Ы˜ВЪУП ‡Т- ФУОУКВМЛfl ФОУ˘‡‰Л, Ф ЛПВМflВПУ„У ·Ы У‚У„У У·У Ы‰У‚‡МЛfl, МВУ·ıУ‰ЛПУИ ЪУ˜МУТЪЛ ЛБПВ ВМЛИ.
СОfl УФ В‰ВОВМЛfl НУМЩЛ„Ы ‡ˆЛЛ ТЪ‚УО‡ ТН‚‡КЛМ˚ ‚ УЪВ˜В- ТЪ‚ВММУИ Ф ‡НЪЛНВ ˜‡˘В ‚ТВ„У Ф ЛПВМfl˛Ъ Ф Л·У ˚ Т ФО‡‚Л- НУ‚УИ НЛТОУЪУИ Л ЛМНОЛМУПВЪ ˚: ФВ ‚˚В ФУБ‚УОfl˛Ъ ЛБПВ-flЪ¸ ОЛ¯¸ БВМЛЪМ˚И Ы„УО, ‡ ‚ЪУ ˚В – БВМЛЪМ˚И Ы„УО Л ‡БЛПЫЪ М‡Ф ‡‚ОВМЛfl ТЪ‚УО‡ ‚ ЪУ˜НВ ЛБПВ ВМЛfl.
иУТОВ УНУМ˜‡МЛfl ·Ы ВМЛfl УФ В‰ВОВММУ„У ЛМЪВ ‚‡О‡ ЛОЛ ‚ТВИ ТН‚‡КЛМ˚ ‡·УЪМЛНЛ Н‡ УЪ‡КМУИ Ф‡ ЪЛЛ В„ЛТЪ Л Ы˛Ъ Ф Л ФУПУ˘Л „ОЫ·ЛММУ„У ЛМНОЛМУПВЪ ‡ ЛБПВМВМЛfl БВМЛЪМУ„У Ы„О‡ Л ‡БЛПЫЪ‡ УТЛ ТЪ‚УО‡ ТН‚‡КЛМ˚ ФУ „ОЫ·ЛМВ Л ТЪ УflЪ ЛМНОЛМУ„ ‡ППЫ, М‡ УТМУ‚‡МЛЛ НУЪУ УИ ‚˚˜В ˜Л‚‡˛Ъ „У ЛБУМ- Ъ‡О¸МЫ˛ Ф УВНˆЛ˛ ТЪ‚УО‡ ТН‚‡КЛМ˚ Т ЫН‡Б‡МЛВП М‡Ф ‡‚ОВМЛfl
ÒТ‚ ‡ М‡ ˛„ Л Т Б‡Ф‡‰‡ М‡ ‚УТЪУН, УЪНОУМВМЛВ Ф УВНˆЛЛ Б‡·Уfl УЪ Ф УВНˆЛЛ ЫТЪ¸fl. аМУ„‰‡ М‡ „ ‡ЩЛНВ ЫН‡Б˚‚‡˛Ъ ı‡-‡НЪВ М˚В „ОЫ·ЛМ˚ ВБНУ„У ЛБПВМВМЛfl ‡БЛПЫЪ‡ ЛОЛ БВМЛЪМУ- „У Ы„О‡, „ ‡МЛˆ „У ЛБУМЪУ‚ Л ПВТЪ ‡‚‡ ЛИ ( ЛТ. 10.24).
аБ Ф Л·У У‚ Т ФО‡‚ЛНУ‚УИ НЛТОУЪУИ М‡Л·УОВВ ‡ТФ УТЪ-‡МВМ Т· ‡Т˚‚‡ВП˚И ‚ ·Ы ЛО¸МЫ˛ НУОУММЫ ‡ФФ‡ ‡Ъ З.Д. иВЪ-УТflМ‡ ( ЛТ. 10.25), Ф ЛМˆЛФ ‰ВИТЪ‚Лfl НУЪУ У„У УТМУ‚‡М М‡ ЪУП, ˜ЪУ ФО‡‚ЛНУ‚‡fl ЛОЛ ЩЪУ ‚У‰У У‰М‡fl НЛТОУЪ‡ М‡ „ ‡МЛˆВ
Ò‚УБ‰ЫıУП Ф УЪ ‡‚ОЛ‚‡ВЪ ( ‡Б˙В‰‡ВЪ) ТЪВНОУ ФУ ФВ ЛПВЪ Ы „У ЛБУМЪ‡О¸МУ„У ПВМЛТН‡.
ëıÂχ ‰ÂÈÒÚ‚Ëfl ˝ÚÓ„Ó Ô Ë·Ó ‡ ÔÓ͇Á‡Ì‡ ̇ ËÒ. 10.26. Ç ÒڇθÌÓÈ ÍÓ ÔÛÒ 1 Ò Í ˚¯Í‡ÏË ÔÓÏ¢ÂÌ Ì‡ ÓÒflı 4 Ò Á‡ÓÒÚ-ÂÌÌ˚ÏË ÍÓ̈‡ÏË ÔÓÎÛˆËÎË̉ 3, ˆВМЪ ЪflКВТЪЛ НУЪУ У„У
ТПВ˘ВМ УЪМУТЛЪВО¸МУ УТЛ НУ ФЫТ‡, ‚ ВБЫО¸Ъ‡ЪВ ˜В„У Ф Л М‡- НОУМВ Ф Л·У ‡ ФУОЫˆЛОЛМ‰ ФУ‚У ‡˜Л‚‡ВЪТfl М‡ УТflı 4 ‰У ЪВı ФУ , ФУН‡ В„У ˆВМЪ ЪflКВТЪЛ МВ Б‡ИПВЪ МЛБ¯ВВ ФУОУКВМЛВ. З ФУОЫˆЛОЛМ‰ В ‡БПВ˘‡ВЪТfl Ф flПУЫ„УО¸М˚И ФВМ‡О 5 Т ВБЛМУ- ‚УИ Ф У·НУИ 6, ‚ Ф‡Б˚ НУЪУ У„У ‚ТЪ‡‚Оfl˛Ъ ТЪВНОflММЫ˛ ФО‡Т- ЪЛМЫ. З ·Ы ЛО¸МУИ НУОУММВ Ф Л·У ˆВМЪ Л ЫВЪТfl ВБЛМУ‚˚ПЛ НУО¸ˆ‡ПЛ 2.
иВ В‰ ТФЫТНУП ‚ ТН‚‡КЛМЫ ФВМ‡О Б‡ФУОМfl˛Ъ М‡ФУОУ‚ЛМЫ
597
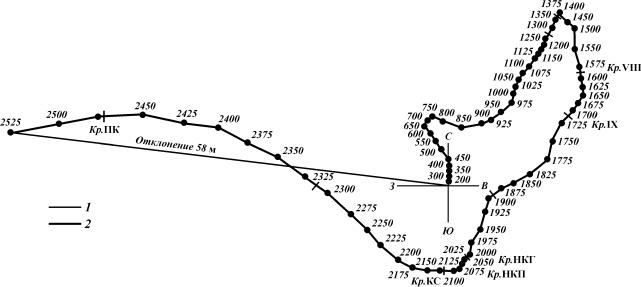
кЛТ. 10.24. п‡ ‡НЪВ М‡fl ЛМНОЛМУ„ ‡ПП‡ ‚В ЪЛН‡О¸МУИ ТН‚‡КЛМ˚, Ф У·Ы ВММУИ ‚ ТОУКМ˚ı „У МУ-„ВУОУ„Л˜ВТНЛı ЫТОУ- ‚Лflı:
1 – „ ‡МЛˆ˚ Т‚ЛЪ Л „У ЛБУМЪУ‚; 2 – Ó·ÓÁ̇˜ÂÌËfl ÏÂÒÚ ‡‚‡ ËÈ
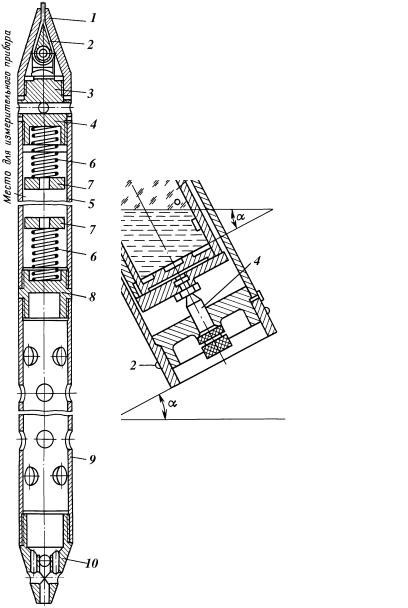
кЛТ. 10.25. ЬВОУМН‡ Т Ф Л·У УП З.Д.#иВЪ УТflМ‡:
1 – ‚В ıМВВ М‡Ф ‡‚ОВМЛВ – Б‡ПУН; 2 – “ ˚·Í‡”; 3 – Ô Ó·Í‡; 4 – Ô ÓÍ·‰Í‡; 5 – ÍÓ ÔÛÒ; 6 – Ô ÛÊË̇; 7 – ‰Â ‚flÌÌ˚ ‰ËÒÍË, ÏÂÊ‰Û ÍÓÚÓ ˚ÏË ‡ÁÏ¢‡ÂÚÒfl ËÁÏ ËÚÂθÌ˚È Ô Ë·Ó ; 8 – ТУВ‰ЛМЛЪВО¸М˚И МЛФФВО¸; 9 – Ú Û·‡; 10 – МЛКМВВ М‡Ф ‡‚ОВМЛВ
êËÒ. 10.26. è Ë·Ó Ç.Ä.#èÂÚ ÓÒfl̇
