
- •Теория принятия решений
- •Оглавление
- •Ключевые слова
- •Основные понятия
- •Часть 1. Принятие решения в условиях определенности Метод анализа иерархий
- •1.1 Постановка задачи
- •1.2 Описание алгоритма решения задачи
- •1.3 Пример решения задачи
- •Часть 2. Принятие решения в условиях неопределенности.
- •2.1 Постановка задачи
- •2.2 Описание алгоритма решения задачи
- •2.3 Пример решения задачи
- •Часть 3. Принятие решения в условиях риска
- •3.1 Постановка задачи
- •3.2 Описание алгоритма решения задачи
- •3.3 Пример решения задачи
- •Часть 4. Марковская задача принятия решений
- •4.1 Постановка задачи
- •4.2 Описание алгоритма решения задачи
- •Модель динамического программирования с конечным числом этапов
- •Модель динамического программирования с бесконечным числом этапов
- •Метод полного перебора
- •Метод итерации по стратегиям без дисконтирования
- •4.3 Пример решения задачи для конечного числа этапов
- •4.4 Пример решения задачи с бесконечным числом этапов методом полного перебора
- •4.5 Пример решения задачи с бесконечным числом этапов методом итерации по стратегиям без дисконтирования
- •Заключение
- •Литература
Модель динамического программирования с конечным числом этапов
При условии, что
количество этапов в задаче выбора
наилучшей стратегии ограничено, эту
задачу можно представить как задачу
динамического программирования с
конечным числом этапов. Пусть число
состояний для каждого этапа равно m.
Обозначим через
![]() оптимальный ожидаемый доход, полученный
на этапах отn
до N
включительно, при условии, что система
находилась вначале этапа n
в состоянии i.
оптимальный ожидаемый доход, полученный
на этапах отn
до N
включительно, при условии, что система
находилась вначале этапа n
в состоянии i.
Обратное рекуррентное
уравнение, связывающее
![]() и
и![]() ,
запишем в виде:
,
запишем в виде:
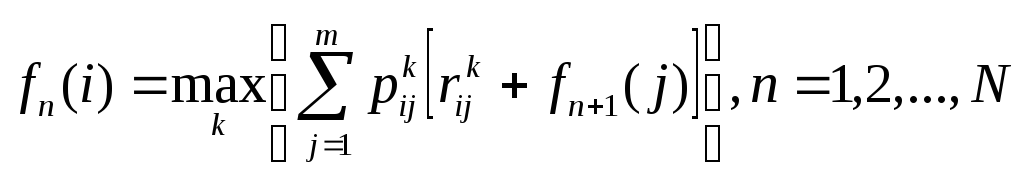 ,
,
где ![]() для всехj.
для всехj.
k – альтернативы.
![]() - вероятности
перехода системы из i
в j
при альтернативе k.
- вероятности
перехода системы из i
в j
при альтернативе k.
![]() - элемент матрицы
доходов R
при переходе системы из i
в j
при альтернативе k.
- элемент матрицы
доходов R
при переходе системы из i
в j
при альтернативе k.
![]() - доход, который
был получен на этапе n+1,
когда система была в состоянии j.
- доход, который
был получен на этапе n+1,
когда система была в состоянии j.
Приведенное
уравнение основано на том, что
накапливающийся доход
![]() получается в результате перехода из
состоянияi
на этапе n
в состояние j
этапе n+1
с вероятностью
получается в результате перехода из
состоянияi
на этапе n
в состояние j
этапе n+1
с вероятностью
![]() .
Введя обозначение
.
Введя обозначение
![]() ,
,
рекуррентное уравнение динамического программирования можно записать следующим образом:
![]() .
.
Для промежуточных значений функция состояния:
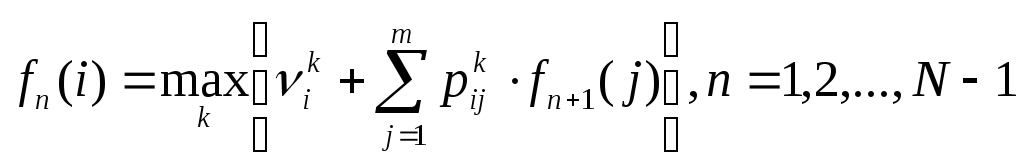 .
.
Модель динамического программирования с бесконечным числом этапов
Поведение Марковского процесса на долгосрочном горизонте характеризуется его независимостью от начального состояния. В этом случае говорят, что система достигла установившегося состояния.
Существует два метода решения таких задач.
Первый метод (метод полного перебора) основан на переборе всех возможных стационарных стратегий в задаче принятия решения. Этот подход можно использовать только тогда, когда общее число стационарных стратегий с точки зрения практических вычисления достаточно мало.
Второй метод ( метод итерации по стратегиям), как правило, более эффективен, так как определяет оптимальную стратегию итерационным путем.
Метод полного перебора
Предположим, что в задаче принятия решений имеется S стационарных стратегий. Пусть PS и RS - матрицы переходных (одношаговых) вероятностей и доходов, соответствующие применяемой стратегии, s=1,2,…, S. Метод перебора включает четыре шага:
Шаг
1.
Вычисляем
![]() - ожидаемый доход, получаемый за один
этап при стратегииs
для заданного состояния i,
i
= 1,2,…,m.
- ожидаемый доход, получаемый за один
этап при стратегииs
для заданного состояния i,
i
= 1,2,…,m.
Шаг
2. Вычисляем
![]() - долгосрочные стационарные вероятности
матрицы переходных вероятностейPS,
соответствующие стратегии s.
Эти вероятности (если они существуют)
находятся из уравнений:
- долгосрочные стационарные вероятности
матрицы переходных вероятностейPS,
соответствующие стратегии s.
Эти вероятности (если они существуют)
находятся из уравнений:
![]()
где
![]()
Шаг 3. Вычисляем ES - ожидаемый доход за один шаг (этап) при выбранной стратегии s:
![]() .
.
Шаг 4. Оптимальная стратегия s* определяется из условия, что
![]()
Метод итерации по стратегиям без дисконтирования
При увеличении числа стационарных стратегий количество комбинаций может оказаться недопустимо большим .Поэтому использование метода полного перебора зачастую не оправдано, так как требует больших затрат машинного времени. Метод итераций по стратегиям лишен этого недостатка.
Метод итераций по стратегиям основывается на следующем. Для любой конкретной стратегии ожидаемый суммарный доход за n-ый этап определяется рекуррентным уравнением.
![]()
Это уравнение и служит основой метода итераций по стратегиям. Однако, чтобы сделать возможным изучение асимптотического поведения процесса, вид уравнения нужно немного изменить. В отличие от величины n, которая фигурирует в уравнении и соответствует i-му этапу, обозначим через η число оставшихся для анализа этапов. Тогда рекуррентное уравнение записывается в виде:
![]()
Здесь
![]() – суммарный ожидаемый доход при условии,
что остались не рассмотреннымиη
этапов. При таком определении η
можно изучить асимптотическое поведение
процесса, полагая при этом, что
– суммарный ожидаемый доход при условии,
что остались не рассмотреннымиη
этапов. При таком определении η
можно изучить асимптотическое поведение
процесса, полагая при этом, что
![]() .
.
Обозначим
через
![]() вектор установившихся вероятностей
состояний с матрицей переходных
вероятностей
вектор установившихся вероятностей
состояний с матрицей переходных
вероятностей![]() и пусть
и пусть![]() — ожидаемый доход за этап, тогда можно
показать, что при достаточно большомη
— ожидаемый доход за этап, тогда можно
показать, что при достаточно большомη
![]() ,
,
где
![]() - постоянный член, описывающий
асимптотическое поведение функции
- постоянный член, описывающий
асимптотическое поведение функции![]() при заданном состоянииi.
при заданном состоянииi.
Так
как
![]() представляет суммарный оптимальный
доход заη
этапов при заданном состоянии i,
а Е
- ожидаемый доход за один этап, то
интуитивно понятно, почему величина
представляет суммарный оптимальный
доход заη
этапов при заданном состоянии i,
а Е
- ожидаемый доход за один этап, то
интуитивно понятно, почему величина
![]() ,
равна сумме
,
равна сумме![]() и поправочного числа
и поправочного числа![]() ,
учитывающего определенное состояниеi.
При этом, конечно, предполагается, что
число η
достаточно велико. Теперь рекуррентное
уравнение можно записать в следующем
виде.
,
учитывающего определенное состояниеi.
При этом, конечно, предполагается, что
число η
достаточно велико. Теперь рекуррентное
уравнение можно записать в следующем
виде.
![]()
Упростив это уравнение, получаем:
![]() ,
,
т.е.
имеем m
уравнений с
![]() неизвестными
неизвестными![]() и E.
и E.
Конечной
целью является определение оптимальной
стратегии, приводящей к максимальному
значению Е.
Так как имеется m
уравнений с
![]() неизвестными, оптимальное значениеЕ
нельзя определить за один шаг. В связи
с этим используется итеративная
процедура, начинающаяся с произвольной
стратегии, а затем определяется новая
стратегия, дающая лучшее значение Е.
Итеративный процесс заканчивается,
если две последовательно получаемые
стратегии совпадают.
неизвестными, оптимальное значениеЕ
нельзя определить за один шаг. В связи
с этим используется итеративная
процедура, начинающаяся с произвольной
стратегии, а затем определяется новая
стратегия, дающая лучшее значение Е.
Итеративный процесс заканчивается,
если две последовательно получаемые
стратегии совпадают.
Итеративный процесс состоит из двух основных шагов.
Шаг 1. Оценивание параметров.
Выбираем произвольную стратегию s. Используя соответствующие матрицы PS и RS произвольно полагая f(m) = 0, решаем уравнения
![]() ,
,
относительно
неизвестных
![]() ,
,![]() .
.
Шаг 2. Улучшение стратегии.
Для каждого состояния определяем альтернативу k, обеспечивающую
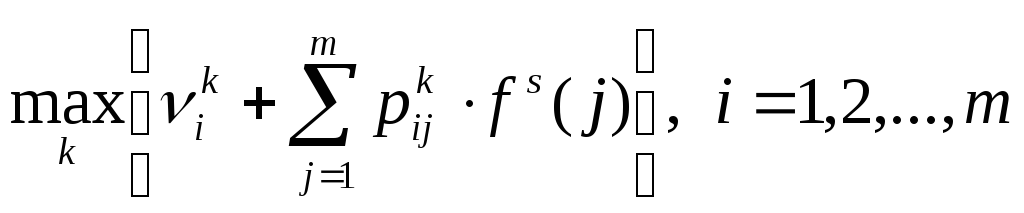
Здесь используются
значения
![]() ,
j = 1, 2, …, m,
определенные на шаге оценивания
параметров. Результирующие оптимальные
решения для состояний 1, 2, …, m
формируют новую стратегию t.
Если s
и t
идентичны, то алгоритм заканчивается;
в этом случае t
– оптимальная стратегия. В противном
случае полагаем s
= t и возвращаемся
к шагу оценивания параметров.
,
j = 1, 2, …, m,
определенные на шаге оценивания
параметров. Результирующие оптимальные
решения для состояний 1, 2, …, m
формируют новую стратегию t.
Если s
и t
идентичны, то алгоритм заканчивается;
в этом случае t
– оптимальная стратегия. В противном
случае полагаем s
= t и возвращаемся
к шагу оценивания параметров.
Оптимизационная задача на шаге улучшения стратегии нуждается в пояснении. Целью этого шага является получение максимального значения Е. Как показано выше,
![]()
Поскольку f(i) не зависит от альтернативы k, задача максимизации на шаге улучшения стратегии эквивалентна максимизации Е по альтернативам k.
