III к. - Электродинамика / Лекции / Лекция 1. Уравнения Максвелла

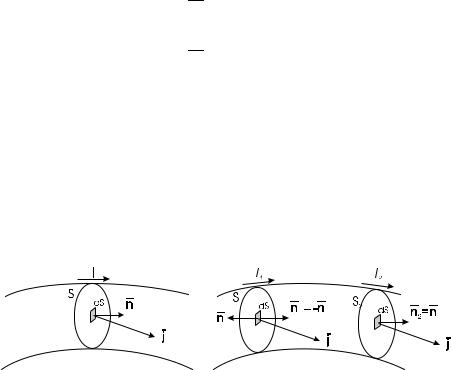
0.1.Список литературы

0.1.Ю.В. Новожилов, Ю.А. Яппа Электродинамика

0.2.Я.П. Терлецкий, Ю.А. Рыбаков Электродинамика

0.3.Дж. Джексон Электродинамика

0.4.Л.Д. Ландау, Е.М. Лифшиц Теория поля

0.5.В.В.Никольский, Т.И.Никольская Электродинамика и распространение радиоволн

0.6.В.В. Батыгин, И.Н. Топтыгин Сборник задач по электродинамике

1

Лекция 1. Уравнения Максвелла

1.1.Заряд, плотность заряда, ток, плотность тока

Источниками электрических и магнитных полей являются покоящиеся и движущиеся заряды. Заряды будем обозначать буквами e, q, Q. Если заряд распределен по некоторому объему, то плотность заряда в некоторой точке объема определяется по формуле

Полный заряд объема может быть найден интегрированием :

Z

Q = ρ dV. (1.2)

V

Рассматривают также распределение зарядов по тонкой поверхности. Тогда вводят поверхностную плотность заряда (отнесенную к единице площади)

При распределении заряда по линии используют линейную плотность заряда (отнесенную к единице длины)

Перемещение зарядов называется током. Ток (сила тока), протекающий через некоторое сечение проводника,

где Q заряд, переносимый через сечение за время t. Ток является скалярной величиной. Для того, чтобы описать перенос заряда в разных сечениях проводника, вводят плотность тока, которая определяется формулой

При протекании тока через проводник плотность тока в различных точках проводника может меняться. В природе выполняется закон сохранения заряда. Вследствие этого изменение плотности заряда связано с плотностью тока уравнением, которое называется уравнением неразрывности. Приведу упрощенный вывод уравнения неразрывности для линейного проводника Рис. 1.2. Если заряды переносимые через сечения S1 и S2 не равны,

то в промежутке между ними накапливается заряд, равный

Z Z

~ ~

Q = jn~1 dS − jn~2 dS t. (1.8)

S1 S2

Этот заряд приводит к изменению плотности. Выражая нормали n~1 и n~2 через нормаль ~n, внешнюю к объему, заключенному между поверхностями S1 и S2, и учитывая, что ток через поверхность проводника равен нулю, получим

Заменяя с помощью теоремы Гаусса поверхностный интеграл на объемный, получаем дифференциальное уравнение неразрывности

∂ρ

∂t

(1.9)

которое в электродинамике должно выполняться всегда.

1.2.Уравнения Максвелла в вакууме.

~

Электрическое поле описывается двумя величинами: вектором напряженности электрического поля E и вето-

~ ~

ром электрической индукции D. Магнитное поле вектором напряженности магнитного поля H и векторои

~

магнитной индккции B. В вакууме они связаны формулами

среды.

Экспериментальные законы электричества и магнетизма были обобщены Максвеллом, который сформулировал уравнения Максвелла. Вся электродинамика построена на решениях уравнений Максвелла. В зависимости от избранной системы единиц в уравнениях Максвела имеются различные коэффициенты. Уравнения Максвелла во всех общепризнанных системах единиц можно получить из их записи в виде

Уравнения могут быть записаны в рационилизированной и нерационализированной формах. В рационализированной форме отсутствует множитель 4π, который в уравнениях (1.11) взят в скобки. Но тогда он чаще появляется в решениях уравнений. В технике рекомендовано применять систему единиц СИ. В СИ напряженности и индукции измеряются в разных единицах. В системе СИ α = 1 и c = 1/√ε0µ0. В теоретической физике удобнее применять гауссову ситему единиц, когда α = c, где c скорость света в вакууме. В гауссовой системе

цах, что удобно. Кроме того в гауссовой системе единиц в решениях уравнений Максвелла нет ε0, µ0, которые в системе СИ появляются в самых неожиданных местах. Для этих лекций я выбрал нерационализированную гауссову систему единиц. При этом выборе в вакууме уравнения Максвелла имеют вид

1.3.Уравнения Максвелла в интегральной форме.

Проинтегрируем уравнение (1.12) по некоторому объему, содержащему заряды Рис. 1.3

Z Z

~

H dV = 4π ρ dV. (1.16)

V V

С помощью теоремы Гаусса интеграл в левой части преобразуем к интегралу по замкнутой поверхности, окружающей объем интегрирования. Интеграл в правой части дает полный заряд q, содержащийся внутри замкнутой поверхности. В результате получаем электростатическую теорему Гаусса.

I

S

Поток вектора электрической индукции через замкнутую поверхность равен величине заряда внутри поверхности, умноженной на 4π.

Аналогичные выкладки в применении к уравнению (1.14) дают результат

I

S

Поток вектора напряженности магнитного поля через любую замкнутую поверхность равен нулю.

Уравнение (1.15) проинтегрируем по поверхности S, опирающейся на контур L, Рис. 1.4

С помощью теоремы Стокса интеграл по поверхности в левой части (1.15) преобразуем в интеграл по контуру

L, на который опирается поверхность. Первый интеграл в правой части (1.15) дает ток I, протекающий через поверхность. Во втором интеграле производную по времени можно вынести за знак интеграла. В результате получим

Циркуляция вектора ~ по замкнутому контуру равна сумме тока, протекающего через ограниченную кон-

H

туром площадь, и производной по времени от потока вектора электрической напряженности через площадь, ограниченную контyром. В статическом случак производная по времени равна нулю, и источником магнитного поля, являетс только ток, протекающий через площадку контура.

Применяя аналогичные выкладки к уравнению (1.13), получим

~

Циркуляция вектора E по замкнутому контуру равна работе по перемещению заряда вдоль контура. Она называется электродвижущей силой. Уравнение (1.21) это закон индукции Фарадея. Э.д.с. в контуре равна проиэводной по времени от потока магнитной индукции через площадку, ограниченную контуром.

1.4.Закон сохранения заряда как следствие уравнений Максвелла.

Уравнение неразрывности (закон сохранения заряда) (1.9) может быть получен из уравнений Максвелла. Т.е. закон сохранения заряда и уравнения Максвелла не противоречат друг другу. Посчитаем дивергенцию от обеих частей урвнения (1.15) и производную по времени от обеих частей уравнения (1.12). В результате получим

Так как дивергенция от ротора равна нулю и частные производные по координатам и времени можно переставлять, то из (1.22) следует уравнение неразрывности (1.9).